岐阜県・公立高校入試 2022年度（ 令和4年度 ）問題編

岐阜県立高校・入学試験学力検査・数学・2022年度

１次の(1)～(6)の問いに答えなさい。

(1)$6-4\times(\,-2\,)\;\;$を計算しなさい。

(2)$3(-x+y)-(2x-y)\;\;$を計算しなさい。

(3)$x=5+\sqrt{\,3\,},\; y=5-\sqrt{\,3\,}\;$ のときの，式 $\;x^{2}+2xy+y^{2}\;\;$ の値を求めなさい。

(4)$2$ 個のさいころを同時に投げるとき，出る目の積が $5$ の倍数になる確率を求めなさい。

(5)連立方程式$\quad\begin{eqnarray}\left\{\begin{array}{l}5x + 2y = 4 \\3x - y = 9 \end{array}\right.\end{eqnarray}\quad$を解きなさい。

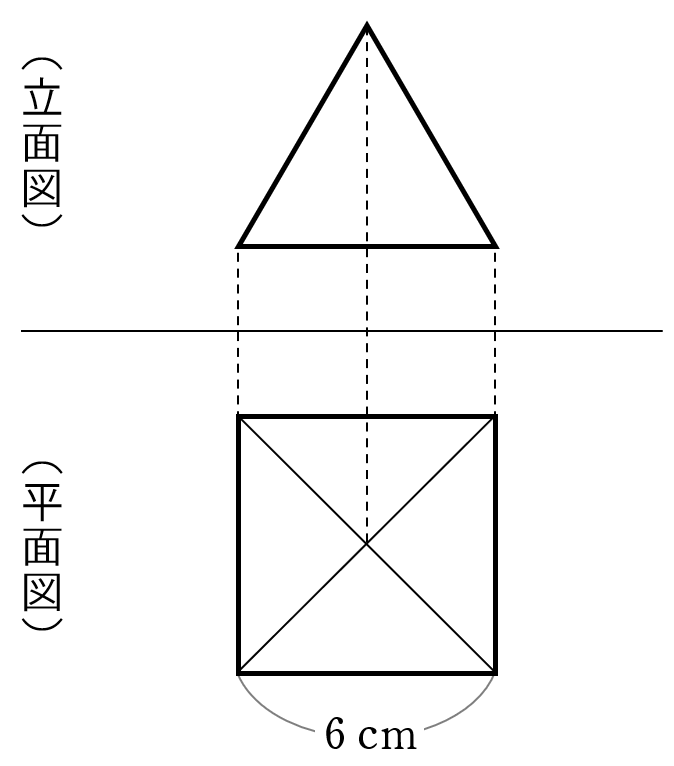
(6)下の図は，正四角すいの投影図である。立面図が正三角形，平面図が $1$ 辺の長さが $6$ cm の正方形であるとき，この正四角すいの体積を求めなさい。

---

２$2$ 次方程式 $\;\;x^{2}+ax-8=0\;\;$ について，次の(1)，(2)の問いに答えなさい。

(1)$a=-1$ のとき，$2$ 次方程式を解きなさい。

(2)$x=1$ が $2$ 次方程式の $1$ つの解であるとき，

(ア)$a$ の値を求めなさい。

(イ)他の解を求めなさい。

---

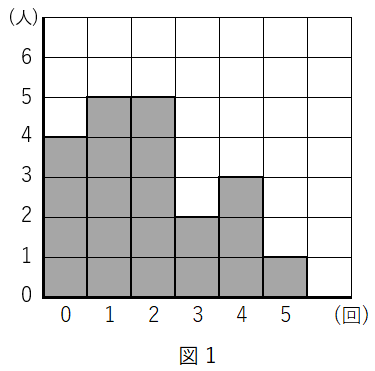
(2)図 1 から，成功した回数の平均値を求めなさい。

(3)バスケットボール部に入部を予定している花子さんも，別の日にシュートを $5$ 回行い，成功した回数を記録した。花子さんの記録を 図 1 に表された記録に加え，成功した回数の平均値と中央値を求めると，$2$ つの値が等しくなった。花子さんの成功した回数を求めなさい。

---

４下の図のような台形 ABCD がある。点 P，Q が同時に A を出発して，P は秒速 $2$ cm で台形の辺上を A から B まで動き，B で折り返して A まで動いて止まり，Q は秒速 $1$ cm で台形の辺上を A から D を通って C まで動いて止まる。P，Q が A を出発してから $x$ 秒後の △APQ の面積を $y$ cm$^{2}$ とする。

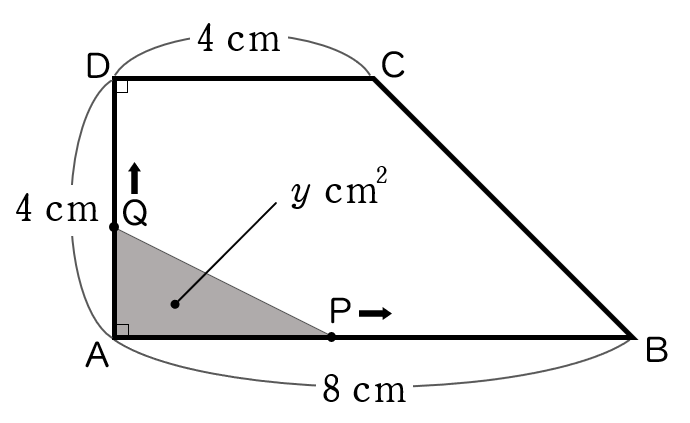
次の (1) ～ (4) の問いに答えなさい。

(1)表中の ア ，イ に当てはまる数を求めなさい。

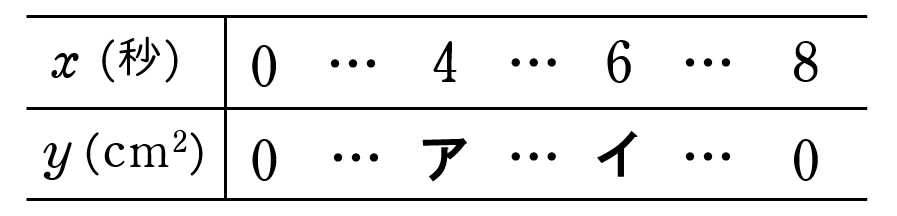
(2)$x$ の変域を次の (ア)，(イ) とするとき，$y$ を $x$ の式で表しなさい。

(ア)$0≦x≦4$ のとき

(イ)$4≦x≦8$ のとき

(3)$x$ と $y$ の関係を表すグラフを書きなさい。( $0≦x≦8$ )

(4)△APQ の面積と，台形ABCD から △APQ を除いた面積の比が，$3:5$ になるのは，P，Q が A を出発してから何秒後と何秒後であるかを求めなさい。

---

５下の図の △ ABC で，点 D は ∠ ABC の二等分線と辺 AC との交点である。
また、点 E は線分 BD の延長線上の点で、CD $=$ CE である。

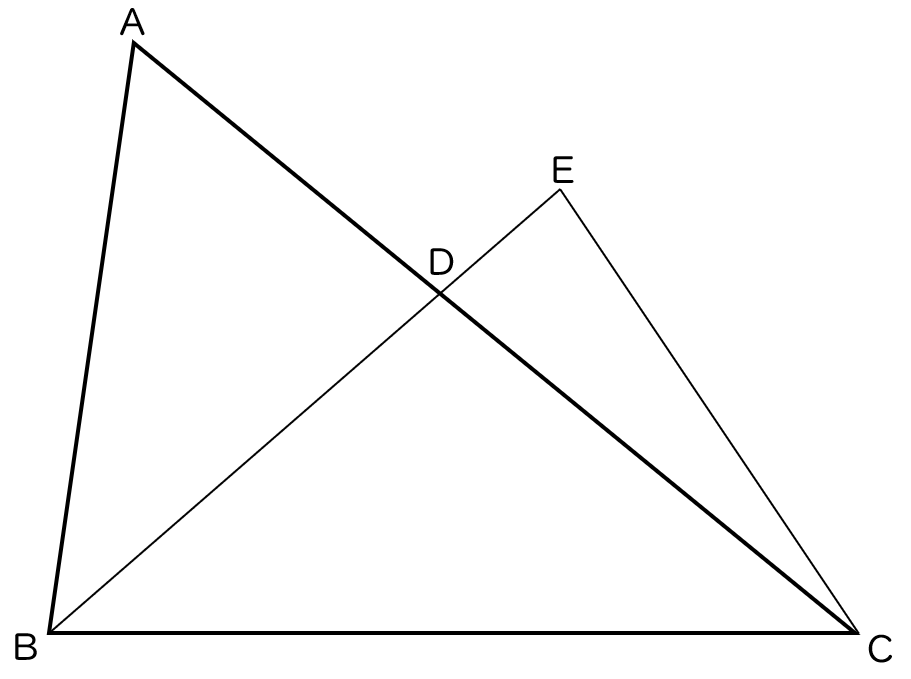
次の (1)，(2) の問いに答えなさい。

(1)△ ABD ∽ △CBE であることを証明しなさい。

(2)AB $=4$ cm，BC $=5$ cm，CA $=6$ cm のとき，

(ア)CE の長さを求めなさい。

(イ)△ ABE の面積は，△ CDE の面積の何倍であるかを求めなさい。

---

６大きな白い紙に，正方形の形に並ぶように連続した自然数を書いていく。まず，$1$ 回目の作業として，$1$ のみを書き，以降，次の作業を繰り返し行う。

$\;\;\;$下の図は，$1$ 回目から $3$ 回目までの作業後の結果である。例えば，$3$ 回目の作業については，新たに書いた自然数は $5$ 個であり，正方形の右下に書いた自然数は $7$ である。

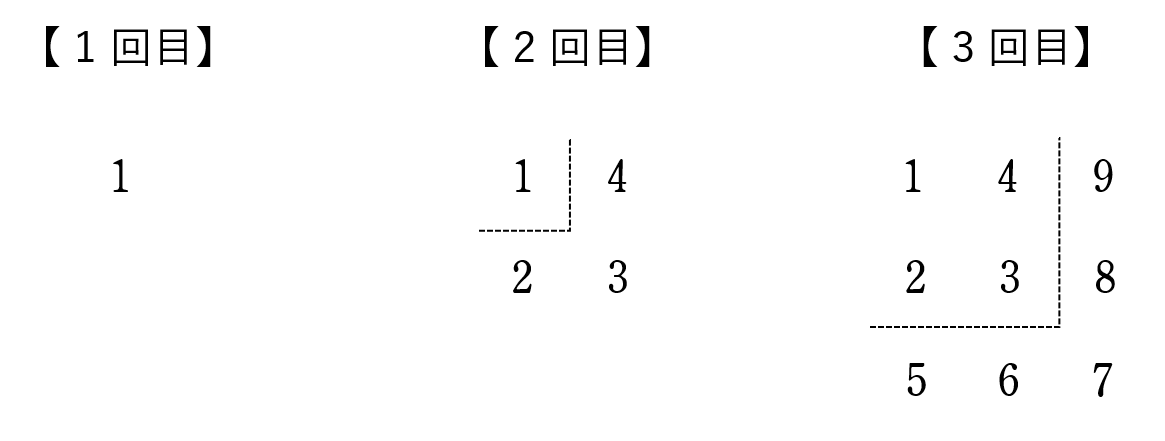
次の (1) ～ (3) の問いに答えなさい。

(1)$5$ 回目の作業について，

(ア)新たに書く自然数の個数を求めなさい。

(イ)正方形の右下に書く自然数を求めなさい。

(2)次の文章は，$n$ が $2$ 以上であるときの $n$ 回目の作業で新たに書く自然数について，太郎さんが考えたことをまとめたものである。ア ～ エ に $n$ を使った式を，それぞれあてはまるように書きなさい。

(3)$10$ 回目の作業について，

(ア)正方形の右下に書く自然数を求めなさい。

(イ)新たに書く自然数の和を求めなさい。