岐阜県・公立高校入試 2021年度( 令和3年度 )問題編
岐阜県立高校・入学試験学力検査・数学・2021年度
1次の(1)~(6)の問いに答えなさい。
(1)$5-3^{2}\;\;$を計算しなさい。
(2)$6xy\div \dfrac{2}{\;3\;}x\;\;$を計算しなさい。
(3)$2$ 次方程式$\quad (\,x-3\,)^{2}=9\quad$を解きなさい。
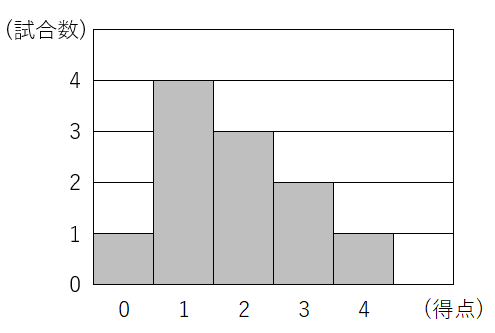
(4)下の図は,あるサッカーチームが,最近の $11$ 試合であげた得点を,ヒストグラムに表したものである。
このヒストグラムについて述べた文として正しいものを,ア ~ エ から $1$ つ選び,符号で書きなさい。
ア中央値と最頻値は等しい。
イ中央値は最頻値より小さい。
ウ中央値と平均値は等しい。
エ中央値は平均値より大きい。
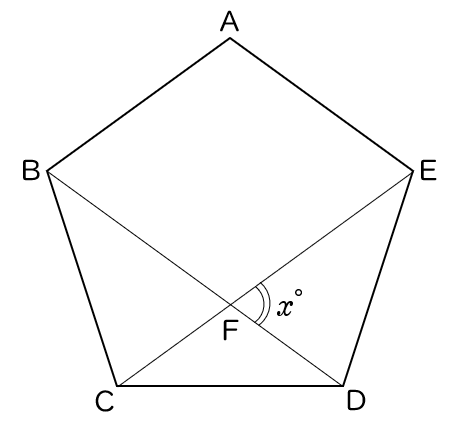
(5)下の図で,五角形 ABCDE は正五角形であり,点 F は対角線 BD と CE の交点である。$x$ の値を求めなさい。
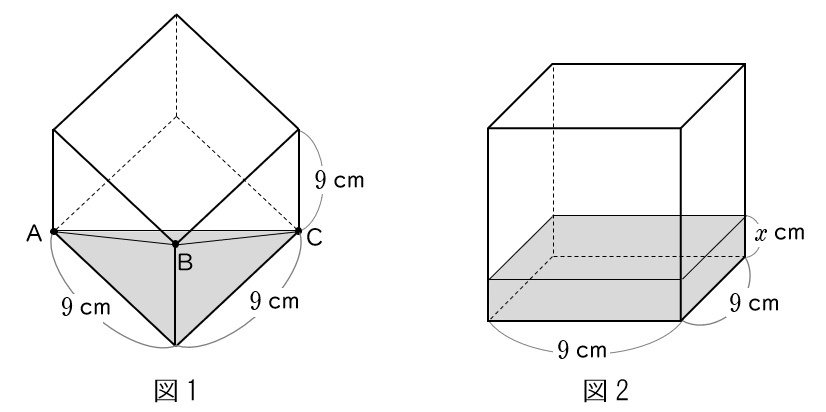
(6)図 1 のように,$1$ 辺の長さが $9$ cmの立方体状の容器に,水面が頂点 A,B,C を通る平面となるように水を入れた。次に,この容器を水平な台の上に置いたところ,図 2 のように,容器の底面から水面までの高さが $x$ cmになった。$x$ の値を求めなさい。
2電子レンジで食品 A を調理するとき,電子レンジの出力を $x$ W,食品 A の調理にかかる時間を $y$ 分とすると,$y$ は $x$ に反比例する。電子レンジの出力が $500$ W のとき,食品 A の調理にかかる時間は $8$ 分である。
次の (1),(2) の問いに答えなさい。
(1)$y$ を $x$ の式で表しなさい。
(2)電子レンジの出力が $600$ W のとき,食品 A の調理にかかる時間は,何分何秒であるかを求めなさい。
3赤と白の $2$ 個のさいころを同時に投げる。このとき,赤いさいころの出た目の数を $a$ ,白いさいころの出た目の数を $b$ として,座標平面上に,直線 $y=ax+b$ をつくる。
例えば,$a=2$ ,$b=3$ のときは,座標平面上に,直線 $y=2x+3$ ができる。
次の (1) ~ (3) の問いに答えなさい。
(1)つくることができる直線は全部で何通りあるかを求めなさい。
(2)傾きが $1$ の直線ができる確率を求めなさい。
(3)$3$ 直線 $y=x+2$,$y=-x+2$,$y=ax+b$ で三角形ができない確率を求めなさい。
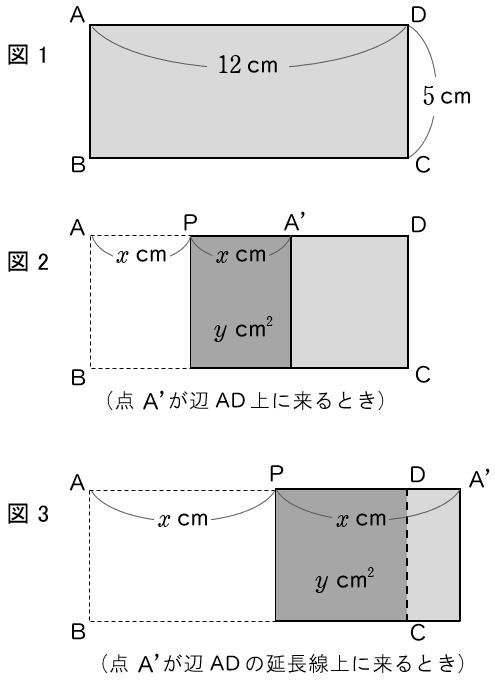
4図 1 のような,縦 $5$ cm,横 $12$ cm の長方形 ABCD のセロハンがある。
辺 AD 上に点 P をとり,点 A が直線 AD 上の点 A’ にくるようにセロハンを点 P で折り返すと,図 2 や図 3 のように,セロハンが重なった部分の色が濃くなった。
AP の長さを $x$ cm,セロハンが重なって色が濃くなった部分の面積を $y$ cm$^{2}$ とする。
次の (1) ~ (4) の問いに答えなさい。
(1)表中の ア ,イ に当てはまる数を求めなさい。

(2)$x$ の変域を次の (ア),(イ) とするとき,$y$ を $x$ の式で表しなさい。
(ア)$0≦x≦6$ のとき
(イ)$6≦x≦12$ のとき
(3)$x$ と $y$ の関係を表すグラフを書きなさい。( $0≦x≦12$ )
(4)セロハンが重なって色が濃くなった部分の面積が,重なっていないセロハンの部分の面積の $2$ 倍になるときがある。このときの AP の長さのうち,最も長いものは何cmであるかを求めなさい。
5下の図で,$4$ 点 A,B,C,D は円 O の周上の点であり,△ ABC は正三角形である。
また,点 E は線分 BD 上の点で,BE $=$ CD である。
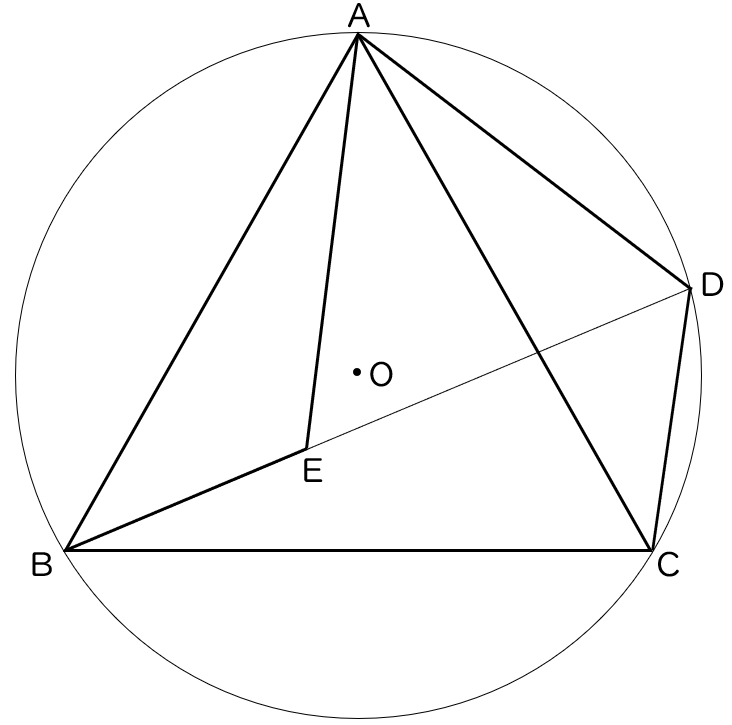
次の (1),(2) の問いに答えなさい。
(1)AE $=$ AD であることを証明しなさい。
(2)点 A から線分 BD にひいた垂線と BD との交点を H とする。
AB $=6$ cm,∠ABD $=45$° のとき,
(ア)AH の長さを求めなさい。
(イ)△ ABE の面積を求めなさい。
6$150$ 枚のカードがある。これらのカードは下の図のように,表には,$1$ から $150$ までの自然数が $1$ つずつ書いてあり,裏には,表の数の,正の平方根の整数部分が書いてある。
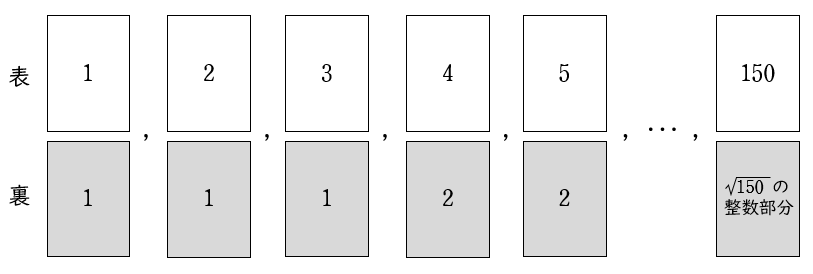
次の (1) ~ (4) の問いに答えなさい。
(1)表の数が $10$ であるカードの裏の数を求めなさい。
(2)次の文章は,裏の数が $n$ であるカードの枚数について,花子さんが考えたことをまとめたものである。
ア,イ には数を,ウ ~ オ には $n$ を使った式を,それぞれあてはまるように書きなさい。
表の数が $150$ であるカードの裏の数は ア であるので,裏の数 $n$ は ア 以下の自然数になる。
(Ⅰ) $\,\; n$ が ア のとき
裏の数が ア であるカードは,全部で イ 枚ある。
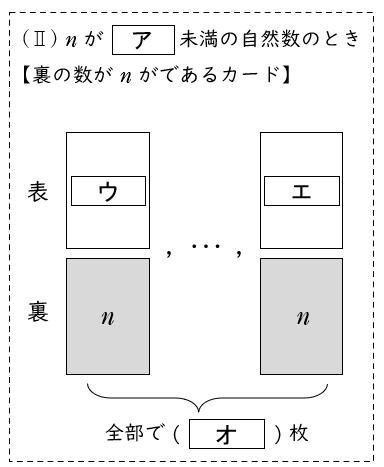
(Ⅱ) $\,\; n$ が ア 未満の自然数のとき
裏の数が $n$ であるカードのうち,最も小さい数は ウ であり,最も大きい数は エ である。
よって,裏の数が $n$ であるカードは,全部で ( オ ) 枚ある。
(3)裏の数が $9$ であるカードは全部で何枚あるかを求めなさい。
(4)$150$ 枚のカードの裏の数を全てかけ合わせた数を $P$ とする。$P$ を $3^{m}$ で割った数が整数になるとき,$m$ に当てはまる自然数のうちで最も大きい数を求めなさい。


