岐阜県・公立高校入試 2022年度( 令和4年度 )解答・解説編
岐阜県立高校・入学試験学力検査・数学・2022年度
1次の(1)~(6)の問いに答えなさい。
(1)$6-4\times(\,-2\,)\;\;$を計算しなさい。
解答・解説
解答$14$
$6\color{red}-4\times(\,-2\,)$乗法から先に計算します
$=6+8$
$=14$
(2)$3(-x+y)-(2x-y)\;\;$を計算しなさい。
解答・解説
解答$-5x+4y$
$3(-x+y)-(2x-y)$
$=-3x+3y-2y\color{red}+\color{black}y$
$=-3x-2x+3y+y$
$=-5x+4y$
(3)$x=5+\sqrt{\,3\,},\; y=5-\sqrt{\,3\,}\;$ のときの,式 $\;x^{2}+2xy+y^{2}\;\;$ の値を求めなさい。
解答・解説
解答$100$
$x+y=(5+\sqrt{\,3\,})+(5-\sqrt{\,3\,})$
$=5+5+\sqrt{\,3\,}-\sqrt{\,3\,}$
$=10$
よって、
$\;x+y=10\;$・・・・・・ ①
$\;x^{2}+2xy+y^{2}=(x+y)^{2}$← ① を代入します
$=10^{2}$
$=100$
(4)$2$ 個のさいころを同時に投げるとき,出る目の積が $5$ の倍数になる確率を求めなさい。
解答・解説
解答$\dfrac{11}{\;36\;}$
$2$ 個のさいころを A、B とすると、目の出方は $6\times6=36$ (通り) です。
A の目と B の目の積を,すべて下の図に表します。
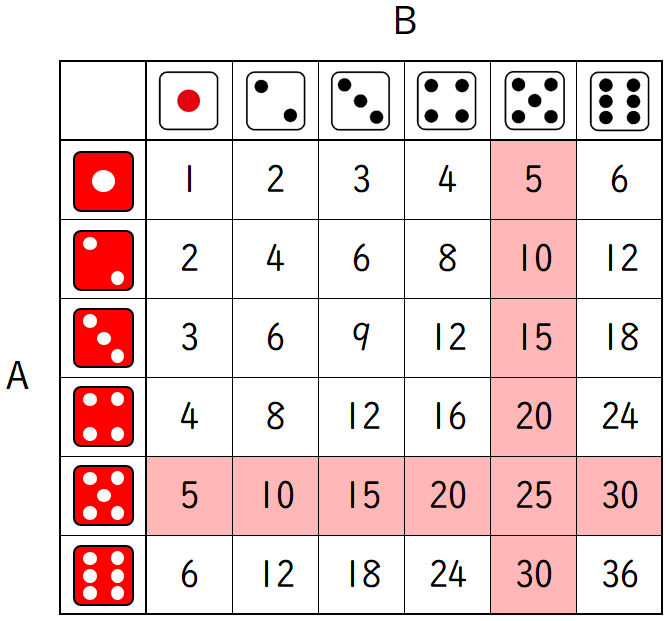
出る目の積が $5$ の倍数になる場合は,上図の塗りつぶしの $11$ 通りです。
よって,出る目の積が $5$ の倍数になる確率は,
$\dfrac{11}{\;36\;}$
(5)連立方程式$\quad\begin{eqnarray}\left\{\begin{array}{l}5x + 2y = 4 \\3x - y = 9 \end{array}\right.\end{eqnarray}\quad$を解きなさい。
解答・解説
ー
解答$\begin{eqnarray}\left\{\begin{array}{l}x=2\\y=-3\end{array}\right.\end{eqnarray}$
$\quad\begin{eqnarray}\left\{\begin{array}{l}5x + 2y = 4&\cdots①& \\3x - y = 9 &\cdots②& \end{array}\right.\end{eqnarray}\;\;$
$\quad\begin{eqnarray}①\qquad\;\;\;\,\;\;\;\;\:5x+2y&=&4\\②\times2\;\;\;+)\;\;6x-2y&=&18\\\hline11x\qquad\;&=&22\\[2pt]x&=&2\end{eqnarray}$
$x=2\;$を①に代入して,
$\begin{eqnarray}5\times2+2y&=&4\\2y&=&-6\\y&=&-3\end{eqnarray}$
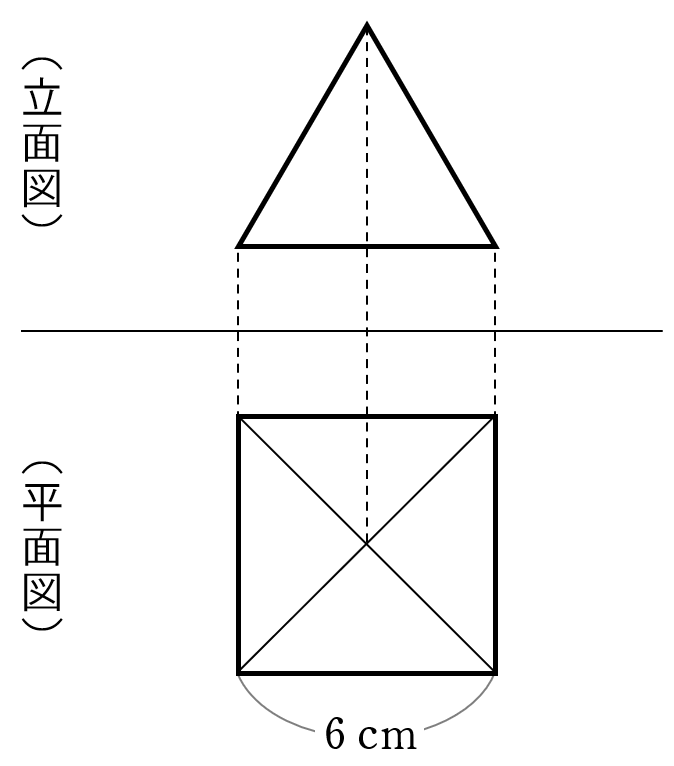
(6)下の図は,正四角すいの投影図である。立面図が正三角形,平面図が $1$ 辺の長さが $6$ cm の正方形であるとき,この正四角すいの体積を求めなさい。
解答・解説
解答$36\sqrt{\,3\,}$ (cm$^{3}$)
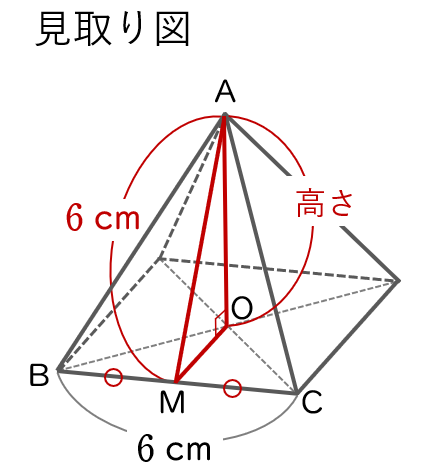
下の図は正四角すいの見取り図と投影図です。図のように頂点 A,B,C をとり,辺 BC の中点を 点 M,底面の対角線の交点を点 O とします。
ここで注意しなくてはいけないのは,
見取り図の 線分 AM の長さは,立面図の 線分 AB の長さと等しいこと
見取り図の 線分 AO の長さ(正四角すいの高さ)は,立面図の線分 AM の長さと等しいこと
です。
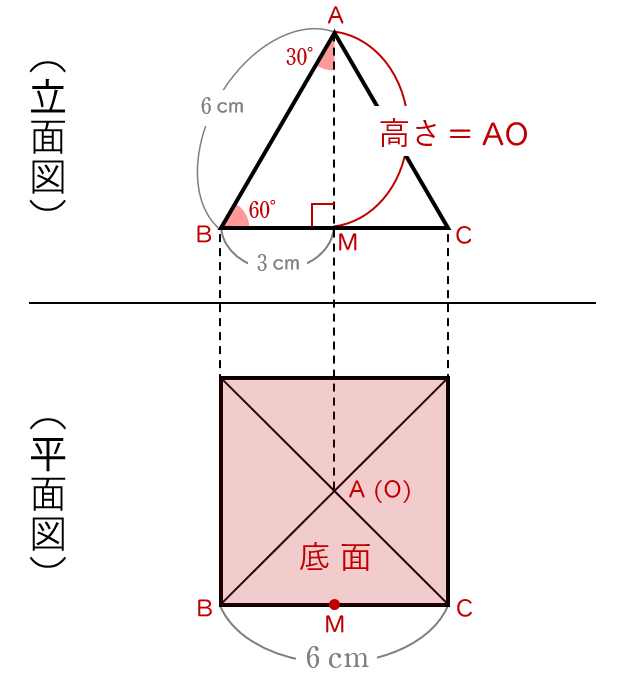
正四角すいの体積を求めるために,まず高さ(AO) を,立面図から求めます。
立面図の △ABM は,$3$ つの角が $30°$,$60°$,$90°$ の直角三角形 (下の図)です。
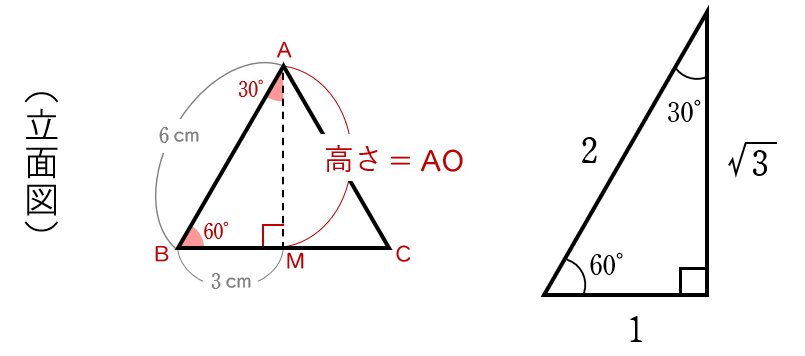
AB:BM:AM $=$ $2$:$1$:$\sqrt{\,3\,}$ $\quad$だから,
BM:AM $=$ $1$:$\sqrt{\,3\,}$
$3$:AM $=$ $1$:$\sqrt{\,3\,}$
AM$\times 1$ $=$ $3\times\sqrt{\,3\,}$
AM $=$ $3\sqrt{\,3\,}$ (cm)
よって,見取り図の線分 AO の長さ,
つまり正四角すいの高さは,$3\sqrt{\,3\,}$ (cm) です。
また,平面図から,正四角すいの底面は $1$ 辺が $6$ cm の正方形であり,その面積は,
$6\times6=36$ (cm$^{2}$)
したがって,
正四角すいの体積 $=$ 底面積 × 高さ(OA) × $\dfrac{1}{\;3\;}$
$= 36\times3\sqrt{\,3\,}\times\dfrac{1}{\;3\;}$
$=36\sqrt{\,3\,}$ (cm$^{3}$)
2$2$ 次方程式 $\;\;x^{2}+ax-8=0\;\;$ について,次の(1),(2)の問いに答えなさい。
(1)$a=-1$ のとき,$2$ 次方程式を解きなさい。
解答・解説
解答$x=\dfrac{\,1\pm\sqrt{\,33\,}\,}{2}$
$a=-1$ のとき,式は,$x^{2}-x-8=0$ です。
差が $-1$ ,積が $-8$ である $2$ つの整数は存在しないので,解の公式で解きます。
$x^{2}-x-8=0$
$x=\dfrac{\,-(-1)\pm\sqrt{\,(-1)^{2}-4\times 1\times (-8)\,}\,}{2}$
$x=\dfrac{\,1\pm\sqrt{\,1+32\,}\,}{2}$
$x=\dfrac{\,1\pm\sqrt{\,33\,}\,}{2}$
(2)$x=1$ が $2$ 次方程式の $1$ つの解であるとき,
(ア)$a$ の値を求めなさい。
解答・解説
解答$a=7$
$2$ 次方程式 $\;x^{2}+ax-8=0\;$ に $x=1$ を代入して,
$1^{2}+a\times 1-8=0$
$1+a-8=0$
$a=7$
(イ)他の解を求めなさい。
解答・解説
解答$x=-8$
(ア)から $a=7$ です。このとき,式は,$x^{2}+7x-8=0$ です。
$x^{2}+7x-8=0$
$(x-1)(x+8)=0$
$x=1$ または $x=-8$
よって,他の解は $-8$
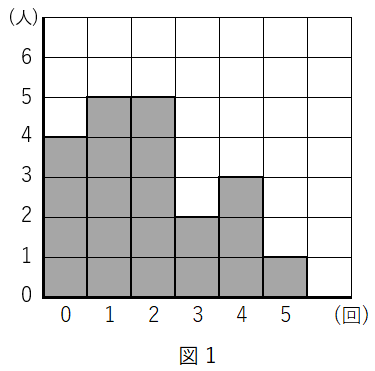
3A 中学校のバスケットボール部は,ある日の練習で,全ての部員がそれぞれシュートを $5$ 回ずつ行い,成功した回数を記録した。図 1 は,その記録をもとに,成功した回数別の人数をグラフに表したものである。
次の (1) ~ (3) の問いに答えなさい。
(1)図 1 から,A 中学校のバスケットボール部の部員の人数を求めなさい。
解答・解説
解答$20$ 人
下はグラフ(ヒストグラム)を度数分布表にしたものです。
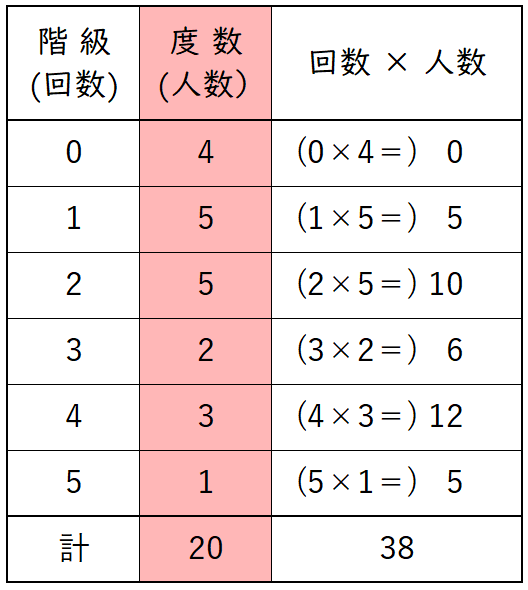
表から、A 中学校のバスケットボール部の部員の人数は $20$ 人です。
(2)図 1 から,成功した回数の平均値を求めなさい。
解答・解説
解答$1.9$ 回
下の度数分布表から,成功した回数の合計は $38$ 回です。
人数の合計は 20 人,成功した回数の合計は 38 回 なので,
成功した回数の平均値は,
$\dfrac{38}{\;20\;}=1.9$ (回)
(3)バスケットボール部に入部を予定している花子さんも,別の日にシュートを $5$ 回行い,成功した回数を記録した。花子さんの記録を 図 1 に表された記録に加え,成功した回数の平均値と中央値を求めると,$2$ つの値が等しくなった。花子さんの成功した回数を求めなさい。
解答・解説
解答$4$ 回
花子さんを加える前の $20$ 人の成功回数を,小さい順に全て並べます。

部員数の合計は $20$ 人 (偶数) なので,
中央値は,小さい方から $10$ 番目(図の⑩)と $11$ 番目(図の⑪)の平均です。
花子さんを加える前の中央値 $=\dfrac{\,2+2\,}{2}=2$
花子さんを加えた後の中央値について,花子さんの成功回数によって場合分けして考えます。
※ 図 2 ,3 の番号は,図 1 で部員につけた番号です。
〔1〕花子さんの成功回数が $0$ 回または $1$ 回のとき
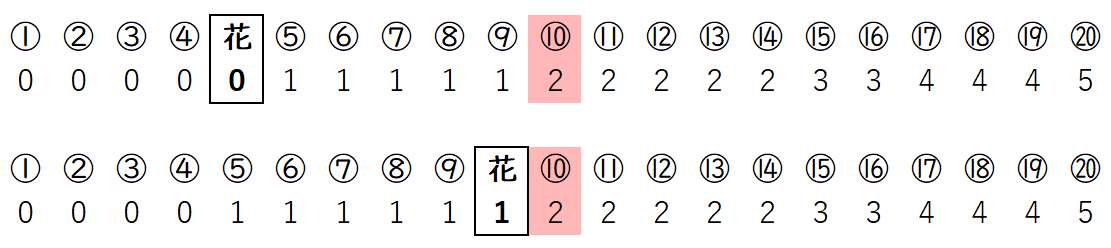
図 2 のように,中央値は 部員⑩ の回数である $2$ になります。
〔2〕花子さんの回数が $2$ 回,$3$ 回,$4$ 回,$5$ 回のとき
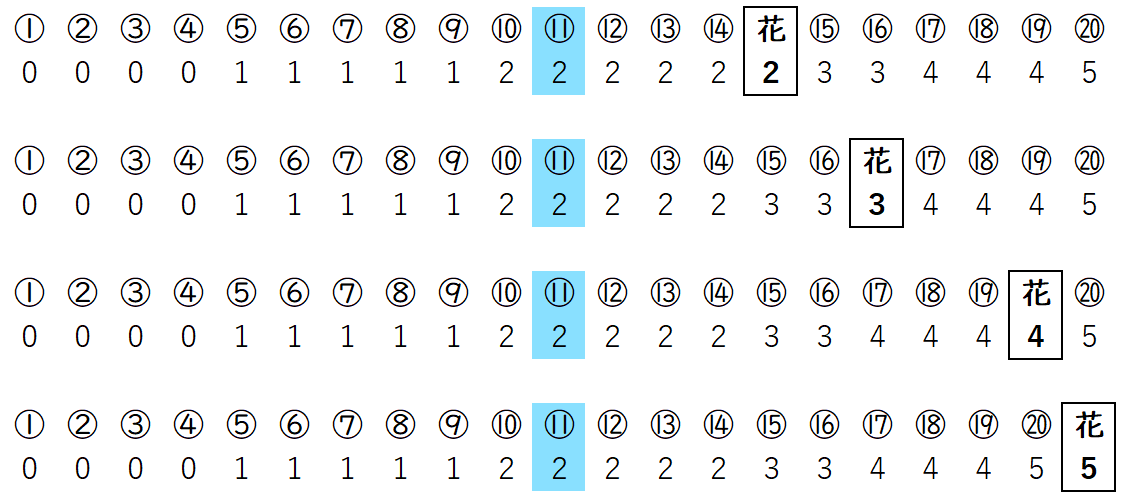
図 3 のように,中央値は 部員⑪ の回数である $2$ になります。
〔1〕,〔2〕から,
花子さんの成功回数が何回だったとしても,花子さんを加えた後の成功回数の中央値は $2$ です。
次に,花子さんの成功回数を $x$ 回だとすると,
(2) の表から,花子さんを加える前の成功回数の合計は $38$ で,
花子さんを加えた後の部員数は $(20+1=)\;21$ 人なので,
花子さんを加えた後の平均値は $\dfrac{\;38+x\;}{21}$と表せます。
問題文から「花子さんを加えた後,平均値と中央値が等しくなった」ので,
$\dfrac{\;38+x\;}{21}=2$
$38+x=42$
$x=4$
4下の図のような台形 ABCD がある。点 P,Q が同時に A を出発して,P は秒速 $2$ cm で台形の辺上を A から B まで動き,B で折り返して A まで動いて止まり,Q は秒速 $1$ cm で台形の辺上を A から D を通って C まで動いて止まる。P,Q が A を出発してから $x$ 秒後の △APQ の面積を $y$ cm$^{2}$ とする。
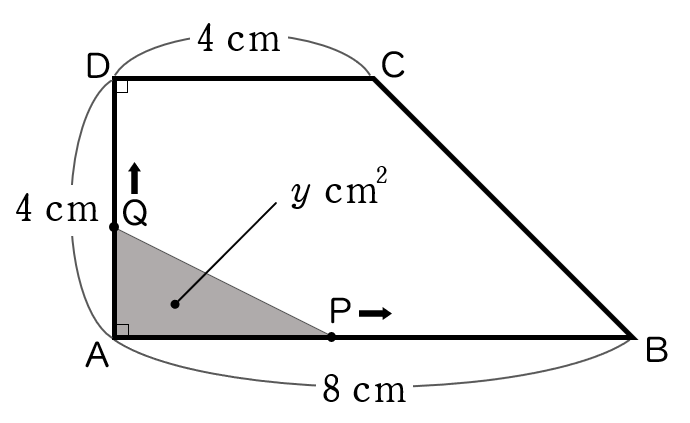
次の (1) ~ (4) の問いに答えなさい。
(1)表中の ア ,イ に当てはまる数を求めなさい。
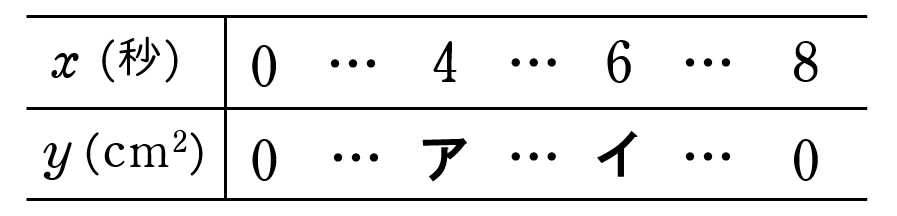
(1) の 解答・解説
解答ア $16$ イ $8$
$x=4$ のとき,下の図のようになります。
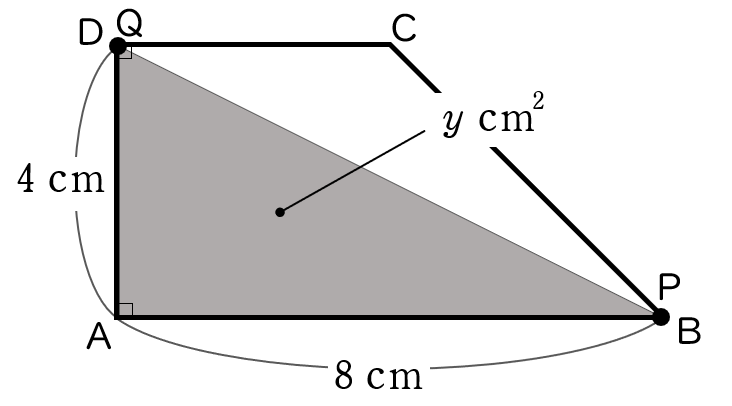
このとき,
$y=8\times 4\times \dfrac{1}{\;2\;} = 16$ア16
$x=6$ のとき,下の図のようになります。
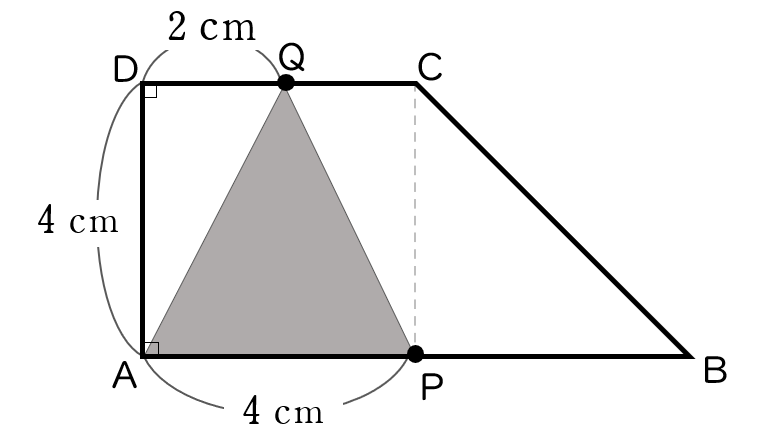
このとき,
$y=4\times 4 \times \dfrac{1}{\;2\;} = 8$イ8
(2)$x$ の変域を次の (ア),(イ) とするとき,$y$ を $x$ の式で表しなさい。
(ア)$0≦x≦4$ のとき
(イ)$4≦x≦8$ のとき
(2) の 解答・解説
解答(ア) $y=x^{2}\quad$(イ) $y=-4x+32$
(ア)$0≦x≦4$ のとき
P は 辺 AB 上を,Q は 辺 AD 上を下の図のように移動しています。
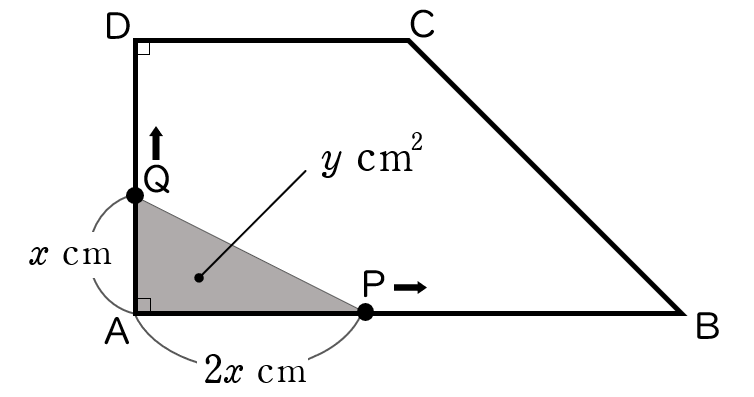
△ APQ は,底辺が $2x$ (cm) ,高さが $x$ (cm) の直角三角形だから,
$y=2x \times x \times \dfrac{\;1\;}{2}$
$=x^{2}$
よって,求める式は式 $\;\;y=x^{2}$ $\;(\,0≦x≦4\,) $
(イ)$4≦x≦8$ のとき
P は 辺 AB 上を,Q は 辺 CD 上を下の図のように移動しています。
※ P は $4$ 秒後に頂点 B に着き,折り返して頂点 A に向かっています。
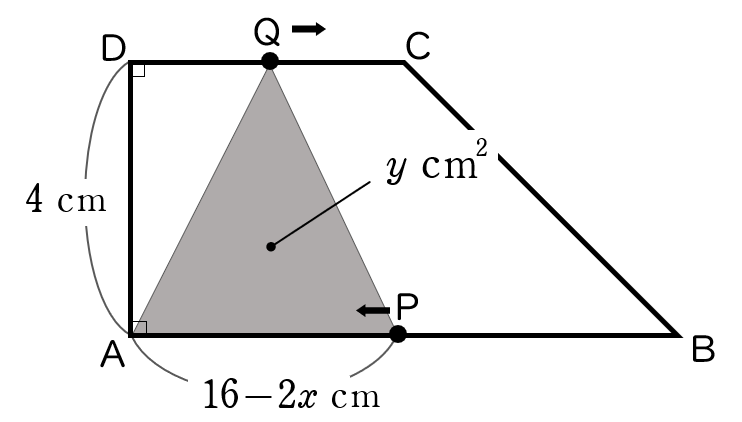
△ APQ は,底辺が $16-2x$ (cm) ,高さが $4$ (cm) の三角形だから,
$y=(16-2x)\times 4 \times \dfrac{\;1\;}{2}$
$=-4x+32$
よって,求める式は式 $\;\;y=-4x+32$ $\;(\,4≦x≦8\,) $
上の図の AP は,A → B → A の $16$ (cm) から,
それまでに P が移動した長さ AB$\;+\;$BP$=2x$ (cm) を引いた長さになります。
(3)$x$ と $y$ の関係を表すグラフを書きなさい。( $0≦x≦8$ )
解答・解説
解答
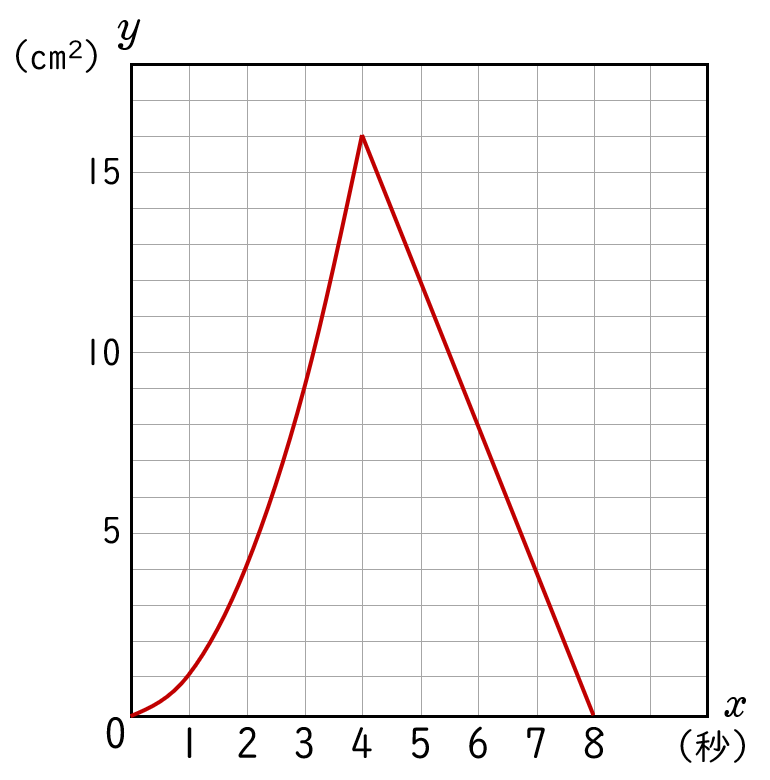
解説
(2) から,
$0≦x≦4$ の範囲では,$y=x^{2}$ のグラフ(放物線)
$4≦x≦8$ の範囲では,$y=-4x+32$ のグラフ(直線)
になります。
(4)△APQ の面積と,台形ABCD から △APQ を除いた面積の比が,$3:5$ になるのは,P,Q が A を出発してから何秒後と何秒後であるかを求めなさい。
解答・解説
解答(ア) $y=x^{2}\quad$(イ) $y=-4x+32$
台形ABCD の面積は,$(4+8)\times 4 \times \dfrac{1}{\;2\;}=24$ cm$^{2}\;$ です。
また,(3) から,△APQ の面積は,$4$ 秒後に最大( $16$ cm$^{2}$ )になります(下図)。
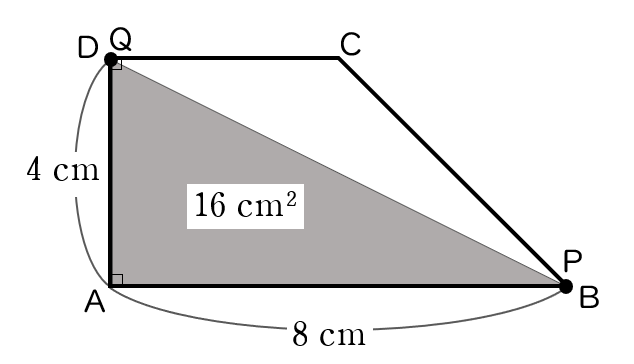
このとき,△APQ の面積は,台形ABCD から △APQ を除いた面積よりも大きくなります。
よって,△APQ の面積と,台形ABCD から △APQ を除いた面積の比が,$3:5$ になるのは,
$0≦x≦4$ のときと,$4≦x≦8$ のときにそれぞれ $1$ 回ずつあることが分かります。
以下,△APQ の面積を $S\small 1$,台形ABCD から △APQ を除いた面積を $S\small 2$ と表します。
〔1〕$0≦x≦4$ のとき
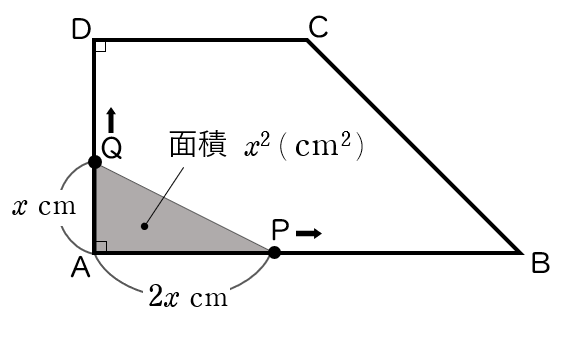
$S\small 1$:$S\small 2\normalsize=x^{2}$:$(24-x^{2})$
求めるのは,$S\small 1$:$S\small 2\normalsize=3$:$5$ になるときだから,
$x^{2}$:$(24-x^{2})=3$:$5$
$5x^{2}=3(24-x^{2})$
$x^{2}=9$
$x=\pm 3$
$0≦x≦4$ だから,$x=3$ よって $3$ 秒後
〔2〕$4≦x≦8$ のとき
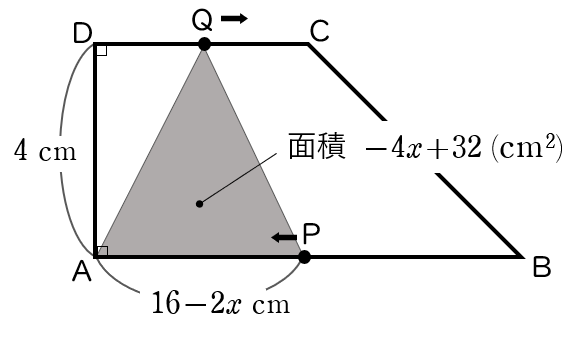
$S\small 1$:$S\small 2\normalsize=(-4x+32)$:$\{24-(-4x+32)\}$
求めるのは,$S\small 1$:$S\small 2\normalsize=3$:$5$ になるときだから,
$(-4x+32)$:$\{24-(-4x+32)\}=3$:$5$
$5(-4x+32)=3(4x-8)$
$-20x+160=12x-24$
$x=\dfrac{\;23\;}{4}=5.75$
$4≦x≦8$ だから適している。よって $5.75$ 秒後
〔1〕,〔2〕から,$S\small 1$:$S\small 2\normalsize=3$:$5$ になるのは $3$ 秒後と$5.75$ 秒後です。
別 解
△APQ の面積と,台形ABCD から △APQ を除いた面積の比が,$3:5$ になるということは,
△APQ の面積と,台形ABCD の面積の比が,$3:(3+5)$ すなわち $3:8$ になるということです。
〔1〕$0≦x≦4$ のとき
△ APQ : 台形ABCD$=x^{2}:24$ だから,
$x^{2}:24=3:8$
$8x^{2}=72$
$x^{2}=9$
$x=\pm 3$
$0≦x≦4$ だから,$x=3$ よって $3$ 秒後
〔2〕$4≦x≦8$ のとき
△ APQ : 台形ABCD$=-4x+32x^{2}:24$ だから,
$(-4x+32):24=3:8$
$8(-4x+32)=72$
$x=\dfrac{\;23\;}{4}=5.75$
$4≦x≦8$ だから適している。よって $5.75$ 秒後
〔1〕,〔2〕から,$S\small 1$:$S\small 2\normalsize=3$:$5$ になるのは $3$ 秒後と$5.75$ 秒後です。
5下の図の △ ABC で,点 D は ∠ ABC の二等分線と辺 AC との交点である。
また、点 E は線分 BD の延長線上の点で、CD $=$ CE である。
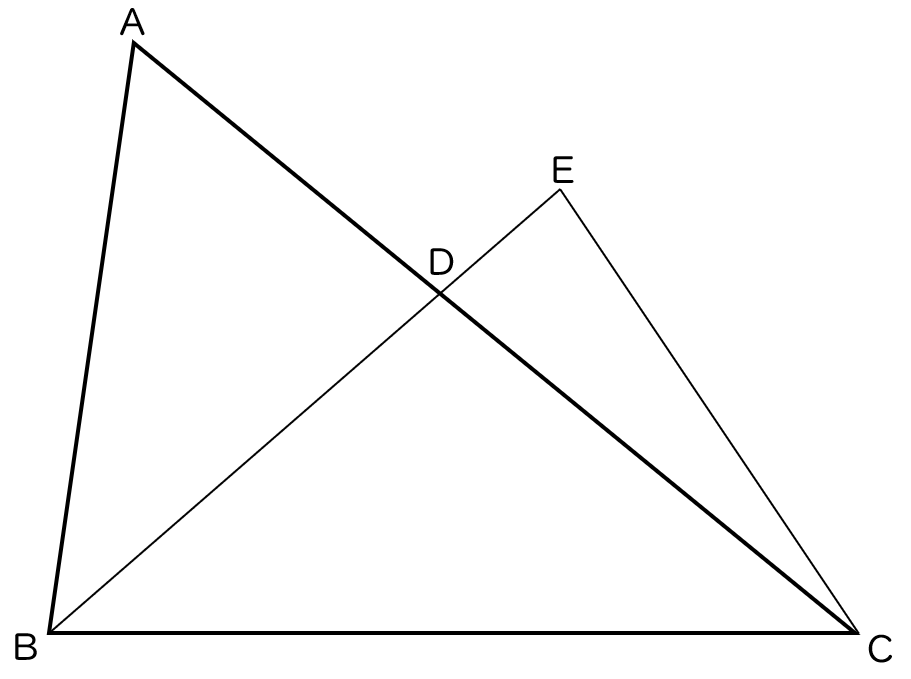
次の (1),(2) の問いに答えなさい。
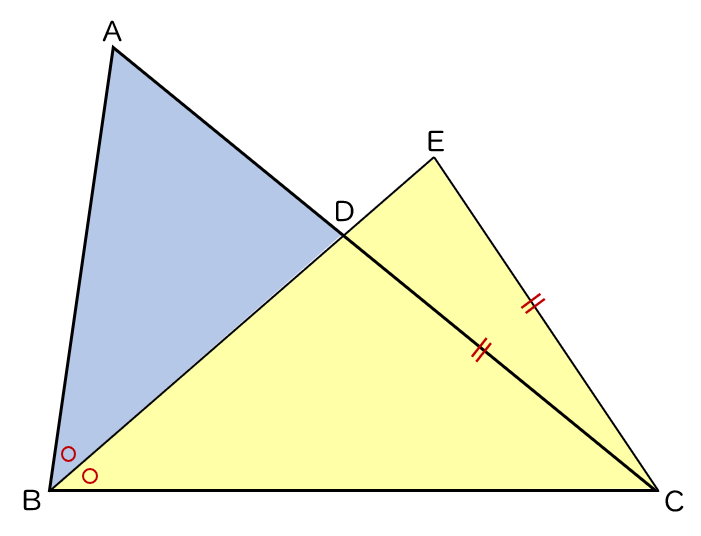
(1)△ ABD ∽ △CBE であることを証明しなさい。
解答
〈仮定〉∠ ABD $=$ ∠CBD,CD $=$ CE
〈結論〉△ ABD ∽ △ CBE
〈証明〉
△ ABD と △ CBE で,
仮定から,∠ABD = ∠CBE・・・・・・①
対頂角は等しいので,
∠ ADB = ∠ CDE・・・・・・②
△ CDE は二等辺三角形だから,
∠ CDE = ∠ CEB・・・・・・③
②,③ から,∠ ADB = ∠ CEB・・・・・・④
①,④ から,$2$ 組の角がそれぞれ等しいので,
△ ABD ∽ △ CBE
(2)AB $=4$ cm,BC $=5$ cm,CA $=6$ cm のとき,
(ア)CE の長さを求めなさい。
解答・解説
解答$\dfrac{\;10\;}{3}$ cm
CE の長さを直接求めることはできませんが,
仮定から CD $=$ CE だから,CD の長さを求めます。
「三角形の角の二等分線と比」の定理(下の右図)を使います。
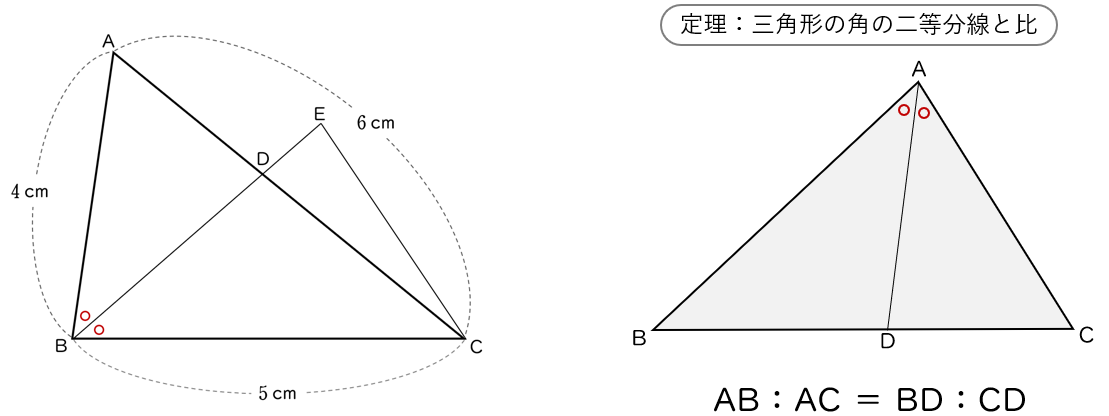
上の左図から,
BA:BC $=$ AD:CD だから,
AD:CD $=$ $4$:$5$ です。
よって,
BA:BC $=$ AD:CD だから,
$\;4\;$:$\;5\;$ $=$ AD:CD
AD:CD $=$ $4$:$5$
CD = AC $\times \dfrac{5}{\;4+5\;}=6 \times \dfrac{\;5\;}{9}=\dfrac{\;10\;}{\;3\;}$
また,CD $=$ CE だから,
CE $=\dfrac{\;10\;}{3}$ (cm)
(イ)△ ABE の面積は,△ CDE の面積の何倍であるかを求めなさい。
解答・解説
解答$\dfrac{\;16\;}{5}$ 倍
AB $:$ CB $=4:5$ だから,
△ABD と △CBE の相似比は $4:5$ ・・・・・・ ①
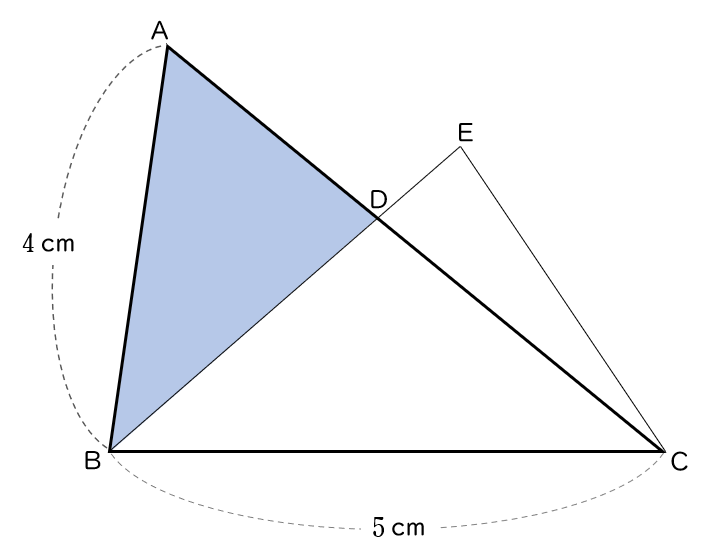
①から,
△ABD と △CBE の面積比は $4^{2}:5^{2}=16:25$
△ABD $:$ △CBE $=16:25$
$25\times$△ABD $=$ $16\times$△CBE
△ABD $=\dfrac{16}{\;25\;}\times$△CBE …… ②
また,①から,
BD $:$ BE $=4:5$
DE $:$ BE $=(5-4):5=1:5$
よって,△CDE と △CBE の面積比は $1:5$
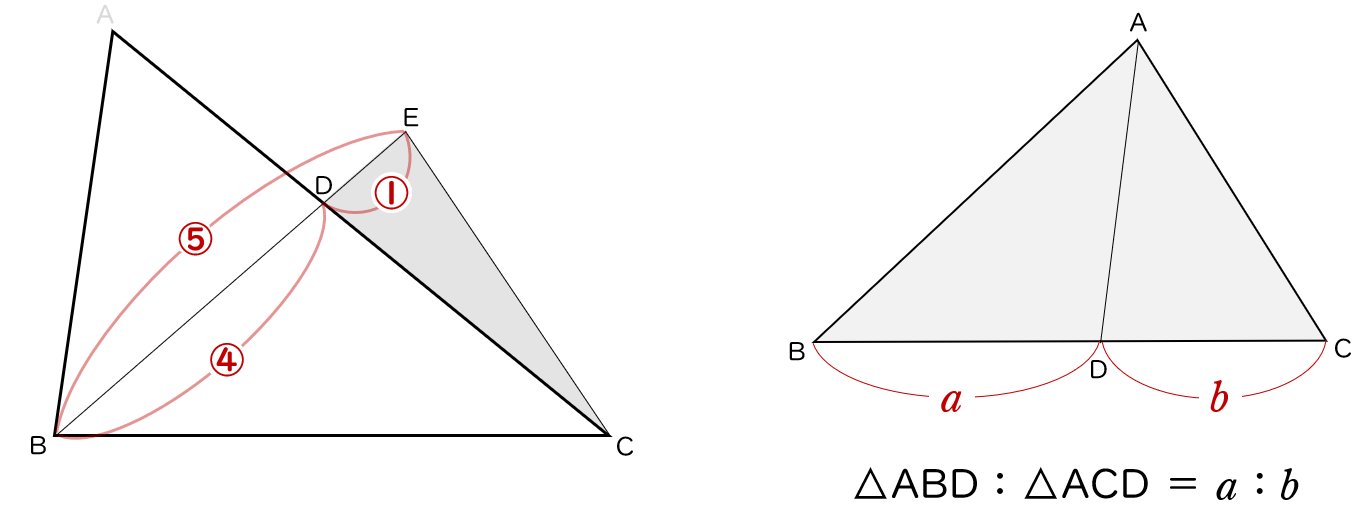
△CDE $:$ △CBE $=1:5$
$5\times$△CDE $=$ $1\times$△CBE
△CDE $=\dfrac{1}{\;5\;}\times$△CBE …… ③
②,③から,
△ABD $:$ △CDE $=$ $\dfrac{16}{\;25\;}\times$△CBE $:$$\dfrac{1}{\;5\;}\times$△CBE
△ABD $:$ △CDE $=16:5$
$5\times$△ABD $=$ $16\times$△CDE
△ABD $=$ $\dfrac{\;16\;}{5}\times$△CDE
したがって,△ABD の面積は,△CDE の $\dfrac{\;16\;}{5}$ 倍です。
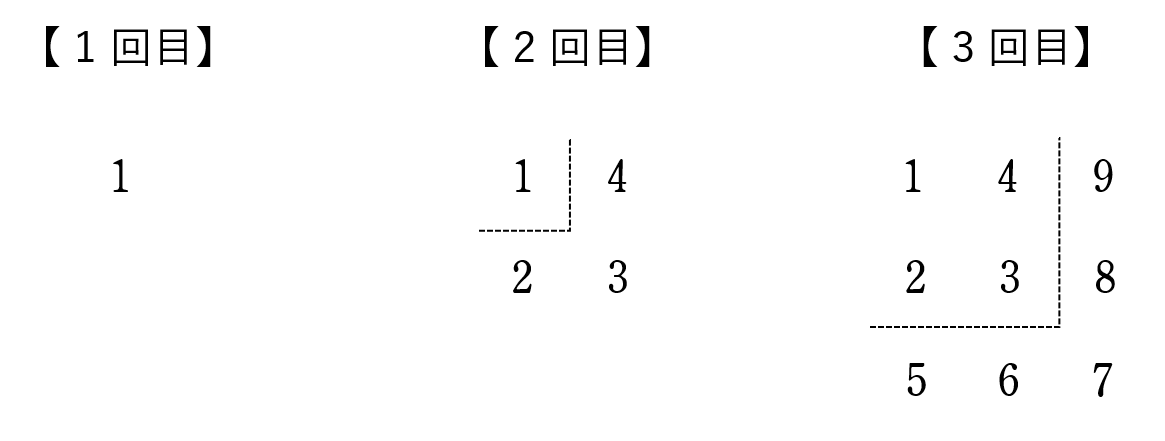
6大きな白い紙に,正方形の形に並ぶように連続した自然数を書いていく。まず,$1$ 回目の作業として,$1$ のみを書き,以降,次の作業を繰り返し行う。
【作業】すでに正方形の形に並んでいる自然数の下側に $1$ 行,右側に $1$ 列を加え,再び正方形の形に並ぶように新たな自然数を書く。自然数は,前の作業で書いた自然数の続きから,まず左下から右下へ,次に右下から右上へ小さい順に書く。
$\;\;\;$下の図は,$1$ 回目から $3$ 回目までの作業後の結果である。例えば,$3$ 回目の作業については,新たに書いた自然数は $5$ 個であり,正方形の右下に書いた自然数は $7$ である。
次の (1) ~ (3) の問いに答えなさい。
(1)$5$ 回目の作業について,
(ア)新たに書く自然数の個数を求めなさい。
(イ)正方形の右下に書く自然数を求めなさい。
(1) の解答・解説
解答(ア) $9$ 個,(イ) $21$
実際に $5$ 回目の作業まで書いてみます。
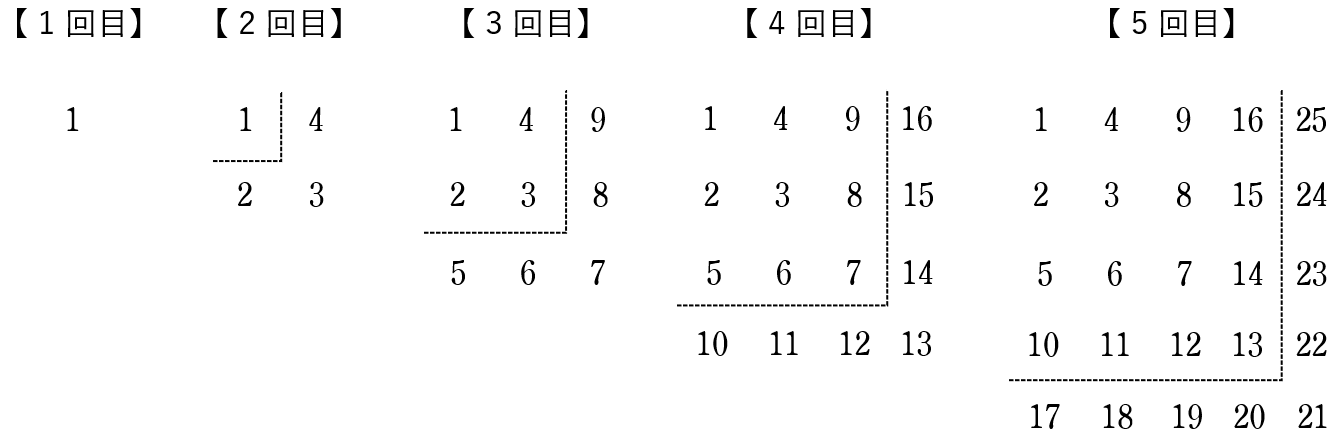
上の図から,$5$ 回目の作業で新たに書く数は $17$ から $25$ までの自然数です。
その個数は
$25-17+1=9$ (個)ア$9$ 個
また,上の図から,右下に書く自然数は $21$ です。イ$21$
実際に書いていく方法では,作業の回数が多くなると対応できません。しかし現実的には,とりあえず (1) だけでも解ければよい,という状況になる場合が多いのではないかと思います。そういった場合は迷わず書いてしまって良いと思います。
「なんらかの規則性に気づかなくては解けない」と思い込んだり考え込んだりせずに,とにかく書いてみる。実際に書いてみると規則性に気づくこともあります。
規則性( $n$ 回目の作業 )については,(2) でくわしく解説します。
(2)次の文章は,$n$ が $2$ 以上であるときの $n$ 回目の作業で新たに書く自然数について,太郎さんが考えたことをまとめたものである。ア ~ エ に $n$ を使った式を,それぞれあてはまるように書きなさい。
$\;\;\;$$n$ 回目の作業で書く最も大きい自然数は ア である。
$\;\;\;$また,$( n-1 )$ 回目の作業で書く最も大きい自然数は イ であるから,$n$ 回目の作業では新たに (ウ) 個の連続した自然数を書くことになる。
$\;\;\;$したがって,$n$ 回目の作業で,正方形の右下に書く自然数は,エ である。
解答・解説
解答ア$\;\;n^{2}$,$\quad$イ$\;\;(n-1)^{2}$,$\quad$ウ$\;\;2n-1$,$\quad$エ$\;\;n^{2}-n+1$
〔1〕最も大きい自然数(以降「最大の数」と表す)について
$n$ 回目の作業で出来る正方形の一辺には,$n$ 個の自然数が並んでいます。
よって,$n$ 回目の作業で出来る正方形に含まれる自然数は,
合計で,$n \times n=n^{2}$ (個)です。
つまり,$1$ から $n^{2}$ までの自然数が並んでいることになります。
したがって,最大の数は $n^{2}$ で,右上にあります。 ア$n^{2}$
〔2〕$n$ 回目の作業で新たに書く自然数の個数(以降「新たに書く個数」と表す)について
〔1〕から,
$(n-1)$ 回目の作業で書いた最大の数は,$(n-1)^{2}$ イ$(n-1)^{2}$
つまり,$1$ から $(n-1)^{2}$ までの自然数が含まれています。
$n$ 回目の作業で書いた最大の数は,$n^{2}$
つまり,$1$ から $n^{2}$ までの自然数が含まれています。
よって,$n$ 回目の作業で,新たに書く個数は,
$n$ 回目までに書いた個数 $-$ $(n-1)$ 回目までに書いた個数
$=n^{2}-(n-1)^{2}$
$=2n-1$ (個) です。 ウ$2n-1$
〔3〕$n$ 回目の作業で正方形の右下に書く自然数(以降「右下に書く数」と表す)について
各作業目で書く自然数は,左下から右へ書き進めるので,
$n$ 回目の作業で右下に書く数は,$n$ 回目の作業で $n$ 番目に書く数,
すなわち,$(n-1)$ 回目の最後の自然数に $n$ を加えた自然数です。
$(n-1)$ 回目の作業で最後に書く数は $(n-1)^{2}$ だから,
$n$ 回目の作業で $n$ 番目に書く数は,
$(n-1)^{2}+n=n^{2}-n+1$ です。エ$n^{2}-n+1$
参 考
| 作 業 | 最大の数 (右上) |
新たに書く 自然数の個数 |
右下の数 |
|---|---|---|---|
| $1$ 回目 | $1=1^{2}$ | $1$ | $1$ |
| $2$ 回目 | $4=2^{2}$ | $3$ | $3$ |
| $3$ 回目 | $9=3^{2}$ | $5$ | $7$ |
| ・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
| $n$ 回目 | $n^{2}$ | $n^{2}-(n-1)^{2}$ $=2n-1$ |
$(n-1)^{2}+n$ $=n^{2}-n+1$ |
(3)$10$ 回目の作業について,
(ア)正方形の右下に書く自然数を求めなさい。
解答・解説
解答$91$
(2) の エ から,$10$ 回目の作業で正方形の右下に書く自然数は,
$n^{2}-n+1$ に $n=10$ を代入して,
$10^{2}-10+1=91$
(イ)新たに書く自然数の和を求めなさい。
解答・解説
解答$1729$
まず$10$ 回目の作業で,新たに書く自然数について調べます。
はじめの数(左下)は,$9$ 回目の作業の最大の自然数より $1$ 大きい。
(2) の ア から,$9$ 回目の作業の最大の自然数は $9^{2}=81$ だから,
・はじめの数(右下)は,$81+1=82$
・最後の数(右上)は,(2) の ア から,$10^{2}=100$
・書いた数の個数は,$100-82\color{red}+1\color{black}=19$ (個)
( または,(2) の ウ から,$2 \times 10-1=19$ )

よって,$10$ 回目の作業で新たに書く自然数の和は,
$82$ から $100$ までの連続した $19$ 個の自然数の和 になります。
$\dfrac{\;82+100\;}{2}\times 19=1729\;$(※下の解説を参照)
〔連続する自然数の和について〕
$a$ から $b$ までの連続する $n$ 個の自然数について,
平均値 = 合計(和) ÷ 個数 だから,
合計(和) = 平均値 × 個数 で求められます。
また,連続するいくつかの自然数の平均値は,
最小の数$(a)$と最大の数$(b)$の平均値 $\dfrac{\;a+b\;}{2}$ になります。よって,
$a$ から $b$ までの連続する $n$ 個の自然数の和は,
$\dfrac{\;a+b\;}{2} \times n$

