岐阜県・公立高校入試 2017年度( 平成29年度 )問題編
岐阜県立高校・入学試験学力検査・数学・2017年度
1次の(1)~(6)の問いに答えなさい。
(1)$-12+2\times(-5)\;\;$を計算しなさい。
(2)$18ab\div\dfrac{\;3\;}{8}a\times b\;\;$を計算しなさい。
(3)$x=\sqrt{5}+\sqrt{2}, \;y=\sqrt{5}-\sqrt{2}\;\;$のときの,式$\;\;x^{2}y-xy^{2}\;\;$の値を求めなさい。
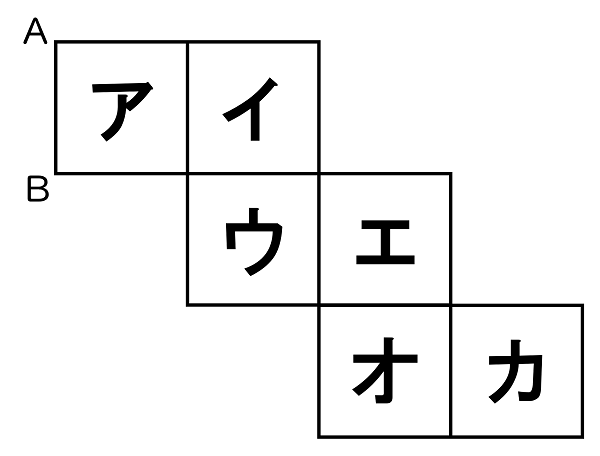
(4)下の図は,立方体の展開図である。この展開図を組み立てて作られる立方体について,辺 AB と垂直な面をア~カの中からすべて選び,符号で書きなさい。
(5)$y\;$の値が正の値をとらない関数を,次のア~エから $1$ つ選び,符号で書きなさい。
ア$\quad y=-\dfrac{x}{\;2\;}\qquad\;$ イ$\quad y=-\dfrac{2}{\;x\;}\qquad\;$ ウ$\quad y=-2x+3\qquad\;\;$ エ$\quad y=-2x^{2}$
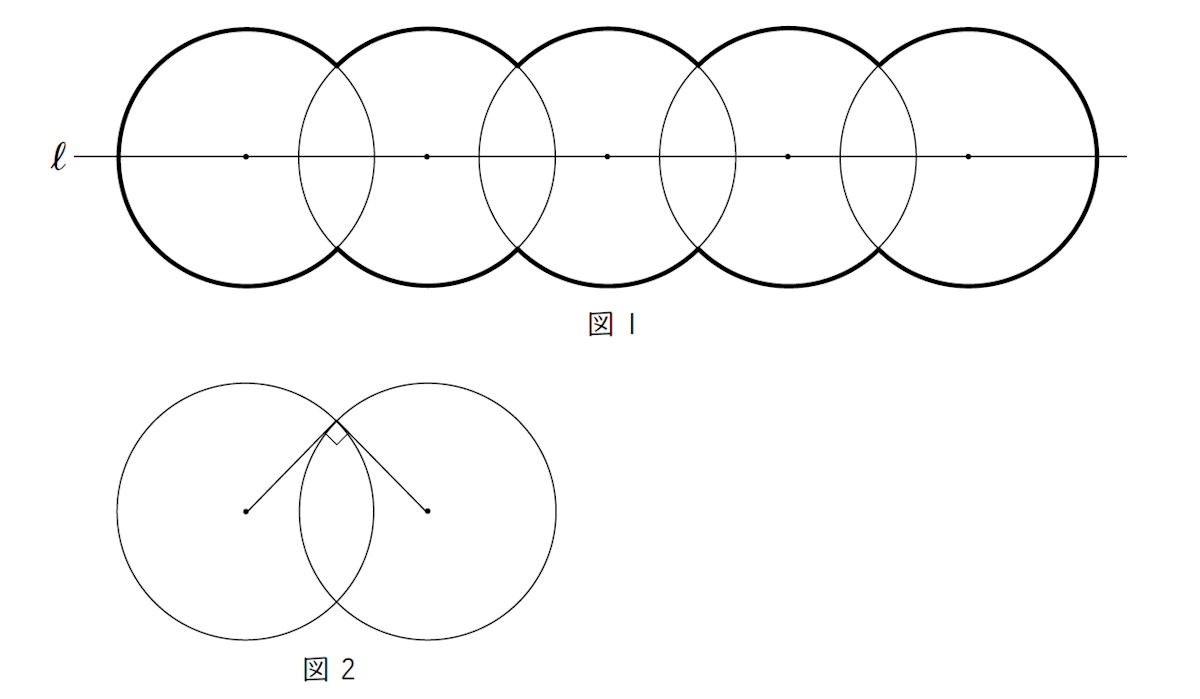
(6)図 1 は,半径 $4$ cm の円を $5$ つ並べた図形で,周を太線で示したものである。この図形では,それぞれの円の中心は直線$\;\ell\;$上にある。また,となり合う $2$ つの円はどれも,図 2 のように,それぞれの円の半径が交点で垂直に交わっている。このとき,図 1 の図形の周の長さを求めなさい。(円周率は$\;\pi\;$を用いなさい。)
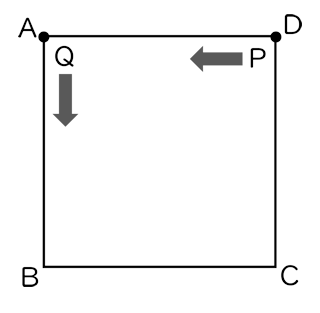
2右図のような,$1$ 辺が $1$ の正方形 ABCD があり,頂点 D に点 P ,頂点 A に点 Q がある。
赤と白の $2$ 個のさいころを同時に $1$ 回投げて,赤いさいころの出た目の数だけ P を左回りに頂点から頂点へ移動させ,白いさいころの出た目の数だけ Q を左回りに頂点から頂点に移動させる。
たとえば,赤いさいころの出た目が $1$ ,白いさいころの出た目が $2$ のときは,P を D → A と移動させ,Q を A → B → C と移動させる。
次の (1)~(3)の問いに答えなさい。
(1)赤と白の $2$ 個のさいころを同時に $1$ 回投げて,P,Q を移動させるとき,P の位置が頂点 B で,Q の位置が頂点 D になる確率を求めなさい。
(2)赤と白の $2$ 個のさいころを同時に $1$ 回投げて,P,Q を移動させるとき,P の位置と Q の位置が同じ頂点になる確率を求めなさい。
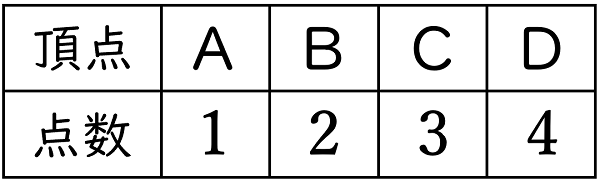
(3)表のように各頂点の点数を決め,P,Q の移動後の位置に応じてそれぞれ得点を与える。赤と白の $2$ 個のさいころを同時に $1$ 回投げて,P,Q を移動させるとき,P の点数が Q の点数よりも高くなる確率を求めなさい。
3濃度が $5$ % の食塩水がある。
次の (1)~(3) の問いに答えなさい。
(1)$400$ g の食塩水 A にふくまれる食塩の重さは何 g であるかを求めなさい。
(2)$400$ g の食塩水 A に,$100$ g の水を加えて,食塩水 B を作った。食塩水 B の濃度を求めなさい。
(3)(2)で作った $500$ g の食塩水 B に,濃度が $9$ % の食塩水 C を混ぜて,濃度が $5$ % の食塩水を作りたい。食塩水 C を何 g 混ぜればよいかを求めなさい。
4図のように,東西にのびるまっすぐな道路上に地点 P と Q がある。
太郎さんは地点 Q に向かって,この道路の地点 P より西を秒速 $3$ m で走っていた。
花子さんは地点 P に止まっていたが,太郎さんが地点 P に到着する直前に,この道路を地点 Q に向かって自転車で出発した。花子さんは地点 P を出発してから $8$ 秒間はしだいに速さを増していき,その後は一定の速さで走行し,地点 P を出発してから $12$ 秒後に地点 Q に到着した。花子さんが地点 P を出発してから $x$ 秒後に進む距離を $y$ m とすると,$x$ と $y$ との関係は表のようになり,$0≦x≦8$ の範囲では,$x$ と $y$ との関係は $y=ax^{2}$ で表されるという。

次の (1)~(5) の問いに答えなさい。
(1)$a$ の値を求めなさい。
(2)表中のア,イにあてはまる数を求めなさい。
(3)$x$ の変域を $8≦x≦12$ とするとき,$x$ と $y$ との関係を式で表しなさい。
(4)$x$ と $y$ の関係を表すグラフを書きなさい。( $0≦x≦12$ )
(5)花子さんは地点 P を出発してから $2$ 秒後に,太郎さんに追いつかれた。
(ア)花子さんが地点 P を出発したとき,花子さんと太郎さんの距離は何 m であったかを求めなさい。
(イ)花子さんは太郎さんに追いつかれ,一度は追い越されたが,その後,太郎さんに追いついた。花子さんが太郎さんに追いついたのは,花子さんが地点 P を出発してから何秒後であったかを求めなさい。
5図のように,長方形 ABCD で,対角線 BD を折り目として △BCD を折り返したところ,頂点 C が点 E に移った。辺 AD と線分 BE との交点を F とする。また,AG は頂点 A から BD にひいた垂線であり,BE と AG との交点を H とする。
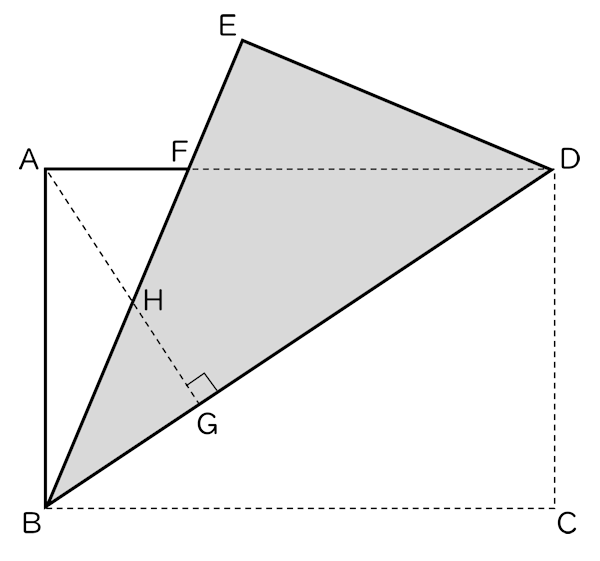
次の (1),(2) の問いに答えなさい。
(1)△ABG ∽ △BDE であることを証明しなさい。
(2)AB $=3$ cm,BC $=4$ cm のとき,
(ア)BG の長さを求めなさい。
(イ)AH の長さを求めなさい。
6数学の授業で,誕生日から数をつくる手順が,先生から次のように示された。
手順①生まれた月の数と生まれた日の数をたす。
②①の結果を $2$ 倍する。
③②の結果に,生まれた月の数の $3$ 倍をたす。
次の (1)~(3) の問いに答えなさい。ただし,$1$ 年は $2$ 月 $29$ 日を含めた $366$ 日とする。
(1)次の文は,先生と $2$ 人の生徒の会話の一部である。ア,ウ,エには数を,イには $x$ ,$y$ を使った式を,それぞれあてはまるように書きなさい。
Aさん:私の誕生日は $3$ 月 $9$ 日だから,手順どおりに数をつくると ア になります。
先生:では,手順どおりにつくった数が, $3$ 月 $9$ 日からつくった数と同じになる日が $1$ 年で他に $2$ 日あるので,見つけてください。
Aさん:どのように考えたらいいですか。
先生:生まれた月の数を $x$ ,生まれた日の数を $y$ として考えてみてください。
Aさん:そうすると,手順どおりにつくった数は イ と表すことができます。
先生:では,その式を使って,$2$ 人で考えてみてください。
Aさん:$y$ の数はそのままで,$x$ の数を $1$ 増やすと, イ の値は $5$ 増えるね。
Bさん:$x$ の数はそのままで,$y$ の数を $1$ 減らすと, イ の値は ウ 減るよ。
Aさん:そうすると,$x$ の数を $1$ 増やしたとき,イ の値が変わらないような $y$ の数はないんだね。
Bさん:$x$ の数を $2$ 増やしたときはどうなるのかな。
Aさん:$y$ の数はそのままで,$x$ の数を $2$ 増やすと,イ の値は $10$ 増えるね。そうすると,$x$ の数を $2$ 増やしたとき,イ の値が変わらないようにするためには,$y$ の数を エ 減らせばいいんだね。
先生:そのことを使うと,手順どおりにつくった数が,$3$ 月 $9$ 日からつくった数と同じになる日を見つけることができますね。
Aさん:わかりました。考えてみます。
(2)手順通りにつくった数が,$3$ 月 $9$ 日から作った数と同じになる日は,何月何日と何月何日であるかを求めなさい。
(3)Cさんは,$1$ 年間のすべての日について手順通りに数を作ったところ,自分の誕生日からつくった数と同じ数になる日が他にはないことがわかった。Cさんの誕生日のように,手順通りにつくった数が,他の日からつくった数と同じにならない日は,$1$ 年間に全部で何日あるかを求めなさい。

