岐阜県・公立高校入試 2018年度( 平成30年度 )問題編
岐阜県立高校・入学試験学力検査・数学・2018年度
1次の(1)~(6)の問いに答えなさい。
(1)$9-6\times 2\;\;$を計算しなさい。
(2)$12ab\div\dfrac{\;3\;}{4}b\;\;$を計算しなさい。
(3)$(\;\sqrt{3}-\sqrt{2}\;)^{2}\;\;$を計算しなさい。
(4)$y$ が $x$ に反比例し,$x=4$ のとき $y=3$ である。$x$ と $y$ の関係を式で表しなさい。
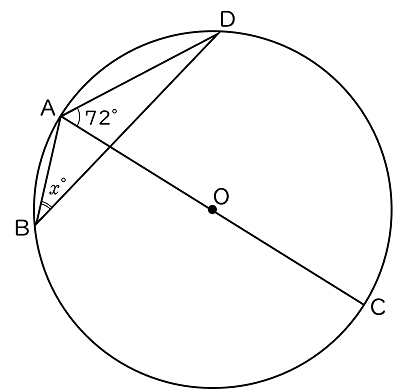
(5)下の図で,$4$ 点 A,B,C,D は円 O の周上にあり,AC は 円 O の直径である。∠CAD $=72°$ のとき,$x$ の値を求めなさい。
(6)$2$ 個のさいころを同時に投げとき,出る目の数の和が $5$ の倍数になる確率を求めなさい。
2ある中学校で読書週間中に,それぞれの生徒が読んだ本の冊数を調べた。右の図は,$1$ 年 $1$ 組の結果をヒストグラムに表したものである。ただし,$1$ 年 $1$ 組の生徒で読んだ本が $8$ 冊以上の生徒はいない。
次の (1) ~ (3) の問いに答えなさい。
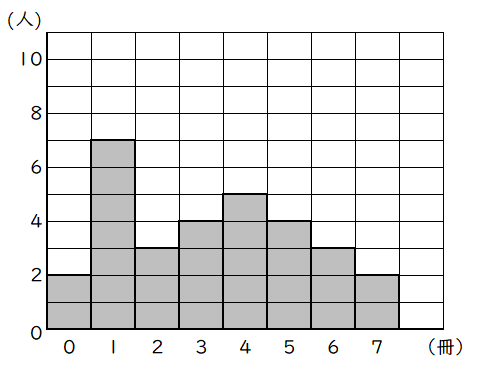
(1)$1$ 年 $1$ 組の生徒の総数は何人であるかを求めなさい。
(2)$1$ 年 $1$ 組のそれぞれの生徒が読んだ本の冊数の中央値を求めなさい。
(3)この中学校の生徒の総数は $200$ 人である。この中学校の生徒で読んだ本が $3$ 冊以上の生徒の相対度数と $1$ 年 $1$ 組の生徒で読んだ本が $3$ 冊上の生徒の相対度数は,同じ値であった。この中学校の生徒で読んだ本が $3$ 冊上の生徒は何人であるかを求めなさい。
3商品 A は,$1$ 個 $120$ 円で売ると $1$ 日あたり $240$ 個売れ,$1$ 円値下げするごとに $1$ 日あたり $4$ 個多く売れるものとする。
次の (1)~(3) の問いに答えなさい。
(1)$1$ 個 $110$ 円で売るとき, $1$ 日で売れる金額の合計はいくらになるかを求めなさい。
(2)$x$ 円値下げするとき,$1$ 日あたり何個売れるかを,$x$ を使った式で表しなさい。
(3)$1$ 個 $120$ 円で売るときよりも,$1$ 日で売れる金額の合計を $3600$ 円増やすためには,$1$ 個何円で売るとよいかを求めなさい。
4学校から公園までの $1400$ m の真っ直ぐな道を通り,学校と公園を走って往復する時間を計ることにした。A さんは学校を出発してから $8$ 分後に公園に到着し,公園に到着後は速さを変えて走って戻ったところ,学校を出発してから $22$ 分後に学校に到着した。ただし,A さんの走る速さは,公園に到着する前と後でそれぞれ一定であった。
次の (1),(2) の問いに答えなさい。
(1)A さんが学校を出発してから $x$ 分後の,学校から A さんまでの距離を $y$ m とすると,$x$ と $y$ との関係は下の表のようになった。

(ア)表中の ア,イ に当てはまる数を求めなさい。
(イ)$x$ と $y$ との関係を表すグラフを書きなさい。( 0 ≦ $x$ ≦ 22)
(ウ)$x$ の変域を $8≦x≦22$ とするとき,$x$ と $y$ との関係を式で表しなさい。。
(2)B さんは A さんが学校を出発してから $2$ 分後に学校を出発し,A さんと同じ道を通って公園まで行き,学校に戻った。このとき,B さんは学校を出発してから $8$ 分後に,公園から戻ってきた A さんとすれ違った。B さんは A さんとすれ違った後,すれ違う前より $1$ 分あたり $10$ m 速く走り,A さんに追いついた。ただし,B さんの走る速さは,A さんとすれ違う前と後でそれぞれ一定であった。
(ア)A さんとすれ違った後の B さんの走る速さは,分速何 m であるかを求めなさい。
(イ)B さんが A さんに追いついたのは,A さんが学校を出発してから何分何秒後であるかを求めなさい。
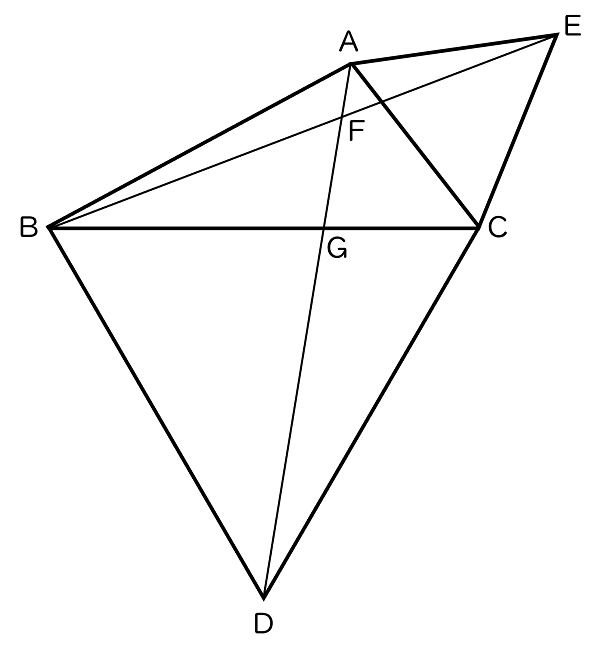
5下の図で,△BDC と △ACE はともに正三角形である。また,線分 AD と BE との交点を F,AD と BC との交点を G とする。
次の (1),(2) の問いに答えなさい。
(1)△ADC ≡ △EBC であることを証明しなさい。
(2)AB $=4$ cm,AC $=4$ cm,BC $=6$ cm のとき,
(ア)DG の長さを求めなさい。
(イ)EF の長さを求めなさい。
6右の表 1 は,かけ算の九九を表にしたものである。太郎さんは,表 1 の太枠の中に書かれた $81$ 個の数字の合計を工夫して求めようとした。
次の (1),(2) の問いに答えなさい。
(1)太郎さんは,表 1 の太枠の中から一部を取り出し,$4$ 段 $4$ 列の表 2 を作った。さらに,表 2 をもとに次のように表 3,表 4,表 5 をそれぞれ作り,表 2 に書かれた $16$ 個の数字の合計を考えた。
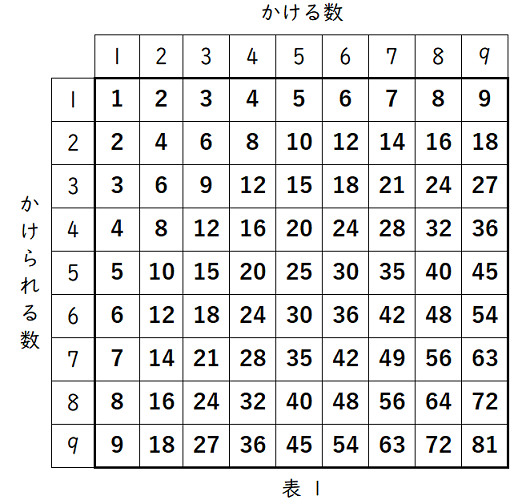
表 3 は,表 2 の数字を左右対称に並べ替えたもの。
表 4 は,表 2 の数字を上下対称に並べ替えたもの。
表 5 は,表 2 の数字を左右対称に並べ替え,さらに上下対称に並べ替えたもの。

次の文章は,太郎さんの考えをまとめたものである。ア,イ,オ,カ には数を,ウ には $b$ を使った式を,エ には $a$ を使った式を,それぞれあてはまるように書きなさい。
表 2,表 3,表 4,表 5 について,各表の上から $3$ 段目,左から $2$ 列目に書かれた数字は,順に,$6$,ア ,$4$,$6$ であり,合計は イ となる。同様に,他の位置に書かれた数字について,各表の上から $a$ 段目,左から $b$ 段目に書かれた数字を $a$,$b$ を使って表すと,順に,$ab$,$a$( ウ ),( エ )$b$,( エ )( ウ ) であり,合計すると オ となる。
したがって,表 2 に書かれた $16$ 個の数字の合計は $\;\sf\dfrac{\,\framebox[1.5cm][c]{オ}\times 16\,}{\framebox[1.5cm][c]{カ}}\;$で計算できる。
(2)表 1 の太枠の中に書かれた $81$ 個の数字の合計を求めなさい。


