岐阜県・公立高校入試 2023年度( 令和5年度 )問題編
岐阜県立高校・入学試験学力検査・数学・2023年度
1次の(1)~(6)の問いに答えなさい。
(1)$2\times(\,-3\,)+3\;\;$を計算しなさい。
(2)$2ab\div\dfrac{b}{\;2\;}\;\;$を計算しなさい。
(3)$(\,\sqrt{\,5\,}-\sqrt{\,3\,}\,\,)^{2}\;\;$を計算しなさい。
(4)$2$ 個のさいころを同時に投げるとき,出る目の和が $6$ の倍数にならない確率を求めなさい。
(5)関数$\;y=-2x^{2}\;$について述べた文として正しいものを,ア ~ エ からすべて選び,符号で書きなさい。
ア$x$ の値が $1$ ずつ増加すると,$y$ の値は $2$ ずつ減少する。
イ$x$ の変域が $-2≦x≦4$ のときと $-1≦x≦4$ のときの,$y$ の変域は同じである。
ウグラフは $x$ 軸について対称である。
エグラフは下に開いている。
(6)線分 AB の垂直二等分線を,定規とコンパスを使って作図しなさい。なお,作図に用いた線は消さずに残しなさい。

2右の図のように,水平に置かれた直方体状の容器 $\rm A$,$\rm B$ がある。$\rm A$ の底面は,周の長さが $20 \, \rm cm$ の正方形で,$\rm B$ の底面は,周の長さが $20 \, \rm cm$ の長方形である。また,$\rm A$ と $\rm B$ の高さは,ともに $40 \, \rm cm$ である。
次の (1) ~ (3) の問いに答えなさい。
(1)$\rm A$ の底面の面積を求めなさい。
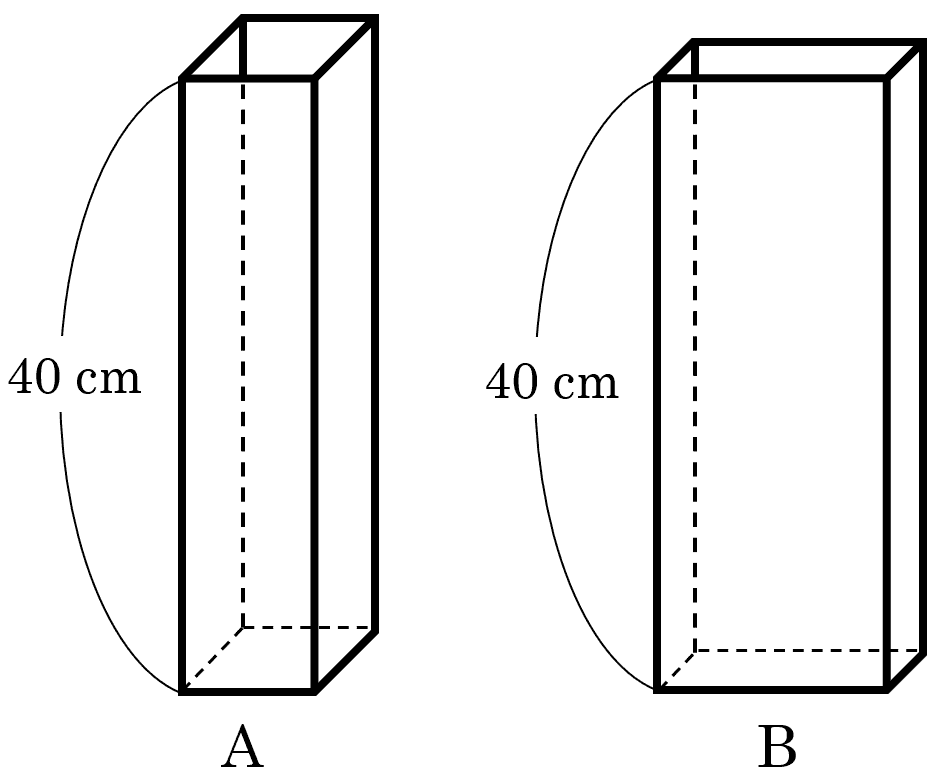
(2)$\rm B$ の底面の長方形の $1$ 辺の長さを $x \, \rm cm$ としたとき,$\rm B$ の底面の面積を $x$ を使った式で表しなさい。
(3)$\rm B$ に水をいっぱいになるまで入れ,その水を全て空の $\rm A$ に移したところ,水面の高さが $30 \, \rm cm$ になった。$\rm B$ の底面の長方形において,短いほうの辺の長さを求めなさい。
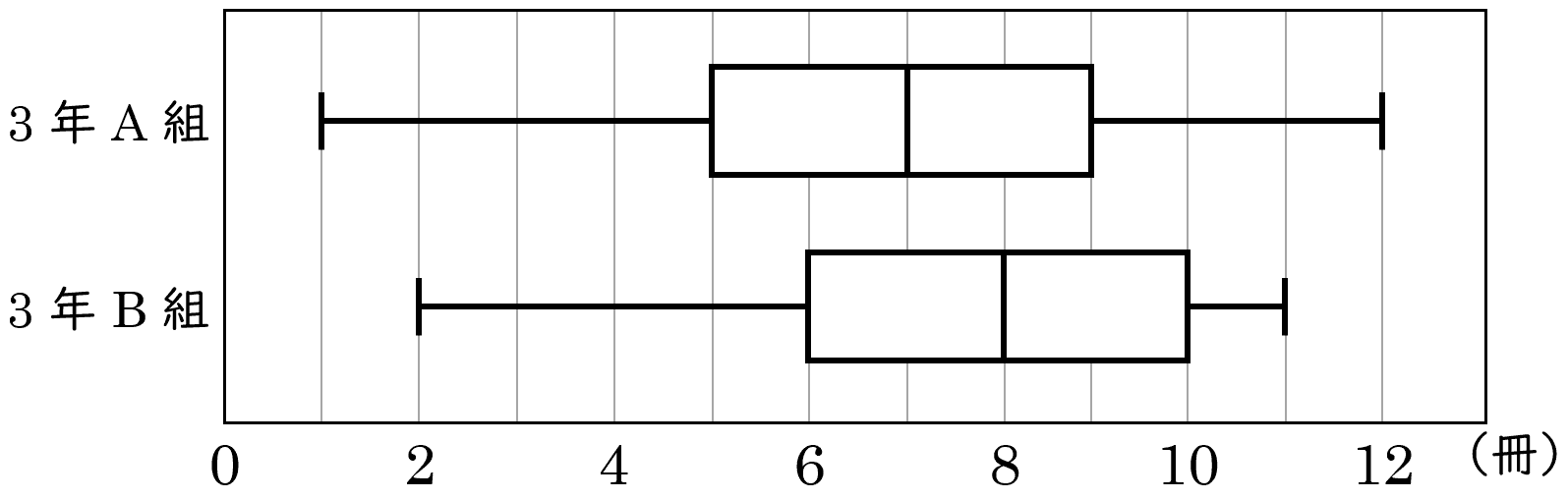
3下の図は,ある中学校の $3$ 年 $\rm A$ 組の生徒 $35$ 人と $3$ 年 $\rm B$ 組の生徒 $35$ 人が $1$ 学期に読んだ本の冊数について,クラスごとのデータの分布の様子を箱ひげ図に表したものである。
次の (1) ~ (3) の問いに答えなさい。
(1)$3$ 年 $\rm A$ 組の第 $1$ 四分位数を求めなさい。
(2)$3$ 年 $\rm A$ 組の 四分位範囲を求めなさい。
(3)図から読み取れることとして正しいものを,ア~エからすべて選び,符号で書きなさい。
ア$3$ 年 $\rm A$ 組と $3$ 年 $\rm B$ 組は,生徒が $1$ 学期に読んだ本の冊数のデータの範囲が同じである。
イ$3$ 年 $\rm A$ 組は,$3$ 年 $\rm B$ 組より,生徒が $1$ 学期に読んだ本の冊数のデータの中央値が小さい。
ウ$3$ 年 $\rm A$ 組は,$3$ 年 $\rm B$ 組より,$1$ 学期に読んだ本が $9$ 冊以下である生徒が多い。
エ$3$ 年 $\rm A$ 組と $3$ 年 $\rm B$ 組の両方に,$1$ 学期に読んだ本が $10$ 冊である生徒が必ずいる。
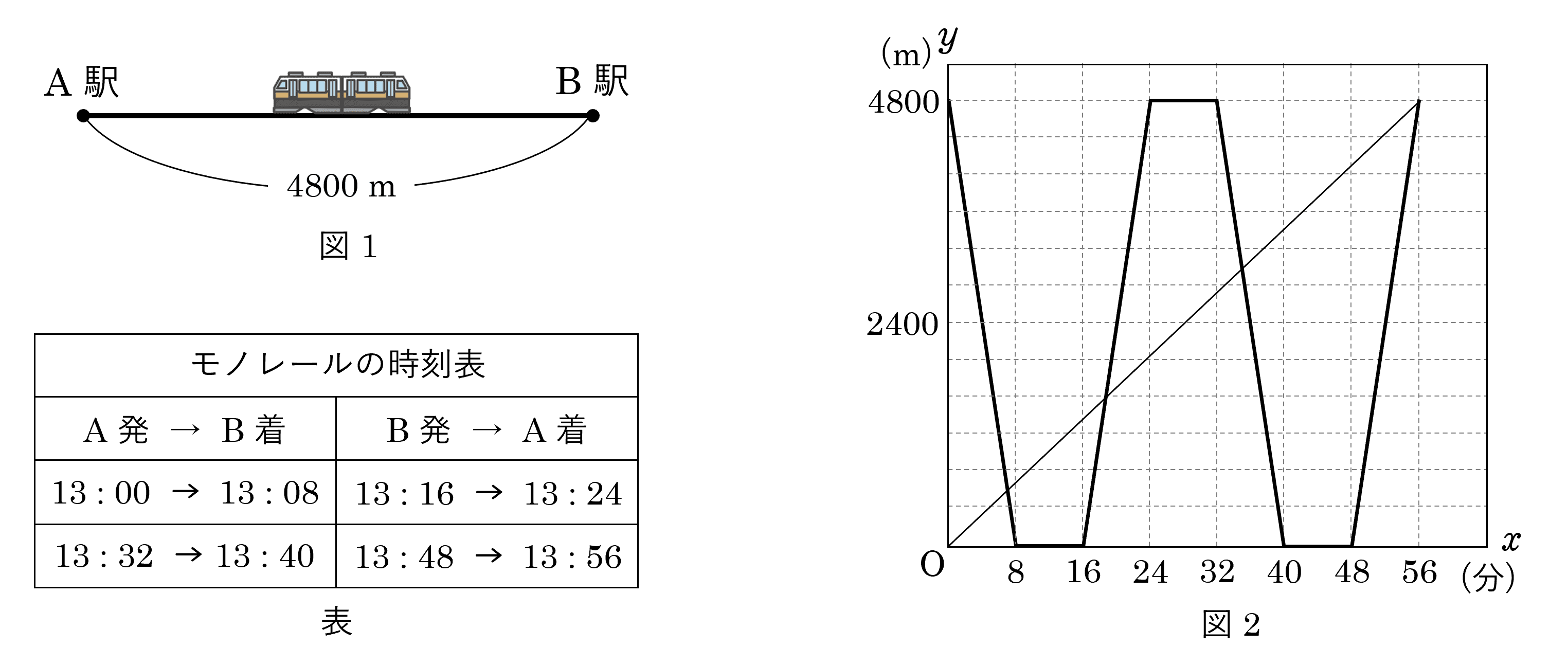
4ある遊園地に,図 $1$ のような,$\rm A$ 駅から $\rm B$ 駅までの道のりが $4800\;\rm m$ のモノレールの路線がある。モノレールは,下の表の時刻にしたがって $\rm A$ 駅と $\rm B$ 駅の間を往復し,走行中の速さは一定である。
モノレールが $13$ 時に $\rm A$ 駅を出発してから $x$ 分後の,$\rm B$ 駅からモノレールのいる地点までの道のりを $y\;\rm m$ とする。$13$ 時から $13$ 時 $56$ 分までの $x$ と$y$ の関係をグラフに表すと,図 $2$ のようになる。
次の (1) ~ (3) の問いに答えなさい。ただし,モノレールや駅の大きさは考えないものとする。
(1)モノレールが $\rm A$ 駅と $\rm B$ 駅の間を走行するときの速さは,分速何 $\rm m$ であるかを求めなさい。
(2)$x$ の変域を次の (ア),(イ) とするとき,$y$ を $x$ の式で表しなさい。
(ア)$0≦x≦8$ のとき
(イ)$16≦x≦24$ のとき
(3)花子さんは $13$ 時に $\rm B$ 駅を出発し,モノレールの線路沿いにある歩道を $\rm A$ 駅に向かって一定の速さで歩いた。花子さんは $\rm B$ 駅を出発してから $56$ 分後にモノレールと同時に $\rm A$ 駅に到着した。
(ア)花子さんが初めてモノレールとすれ違ったのは,モノレールが $13$ 時に $\rm A$ 駅を出発してから,何分後であったかを求めなさい。
(イ)花子さんは,初めてモノレールとすれ違った後,A 駅に向かう途中で,B 駅から戻ってくるモノレールに追い越された。花子さんが初めてモノレールとすれ違ってから途中で追い越されるまでに,歩いた道のりは何 $\rm m$ であったかを求めなさい。
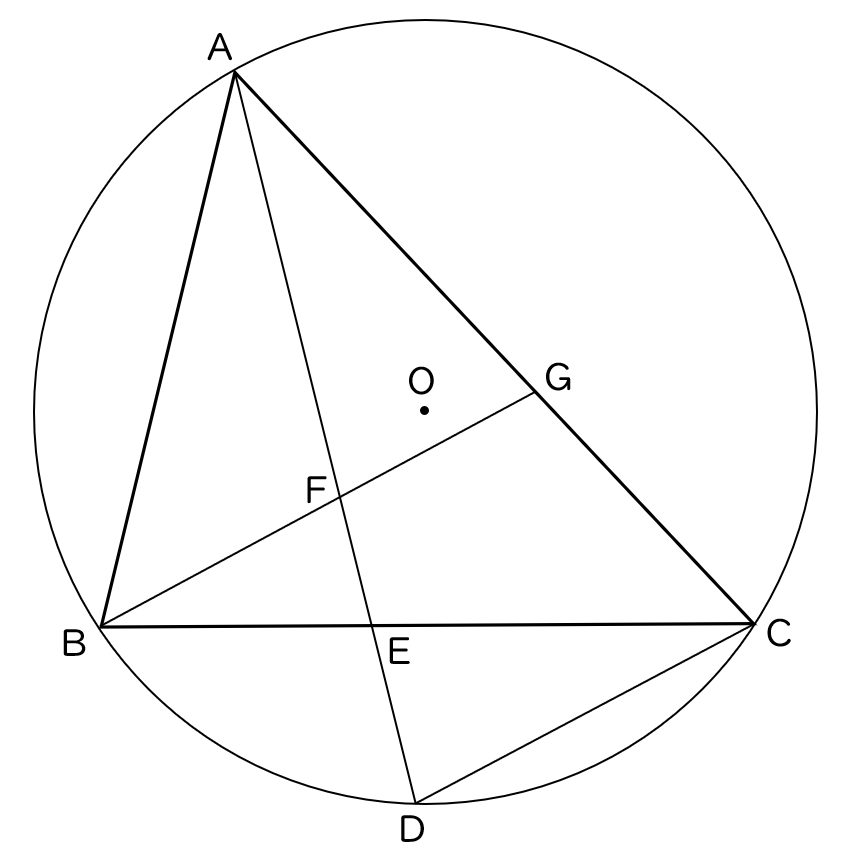
5下の図で, △ ABC の $3$ つの頂点 A,B,C は円 O の周上にあり,点 D は ∠ BAC の二等分線と円 O との交点である。また,線分 AD と辺 BC の交点を E とし,B を通り線分 DC に平行な直線と AD,辺 AC との交点をそれぞれ F,G とする。
次の (1),(2) の問いに答えなさい。
(1)△ AEC ∽ △ BGC であることを証明しなさい。
(2)AB $=4\;\rm cm$,BC $=5\;\rm cm$,CA $=6\;\rm cm$ のとき,
(ア)CE の長さを求めなさい。
(イ)△ BEF の面積は,△ AFG の面積の何倍であるかを求めなさい。
6$10$ 以上の自然数について,次の作業を何回か行い,$1$ けたの自然数になったときに作業を終了する。
【作業】自然数の各位の数の和を求める。
$\;\;\;$例えば,$99$ の場合は,〈 例 〉のように自然数が変化し,$2$ 回目の作業で終了する。
〈 例 〉$\;\;$$99\quad\longrightarrow\quad18\quad \longrightarrow\quad9$
次の (1) ~ (5) の問いに答えなさい。
(1)$1999$ の場合は,作業を終了するまでに自然数がどのように変化するか。〈 例 〉にならって書きなさい。
(2)$10$ 以上 $30$ 以下の自然数のうち,$2$ 回目の作業で終了するものを全て書きなさい。
(3)次の文章は,$3$ けたの自然数の場合に何回目の作業で終了するかについて,太郎さんが考えたことをまとめたものである。ア には $a$,$b$,$c$ を使った式を,イ ,ウ には数を,それぞれあてはまるように書きなさい。
$\;\;\;$$3$ けたの自然数の百の位の数を $a$,十の位の数を $b$,一の位の数を $c$ とすると,$1$ 回目の作業でできる自然数は, ア と表すことができる。ア の最小値は $1$ で,最大値は イ である。
① $\;\;$ア が $1$ けたの自然数のとき
$1$ 回目の作業で終了する。
② $\;\;$ア が $2$ けたの自然数のとき
$1$ 回目の作業では終了しない。作業を終了するためには,ア が ウ のときはあと $2$ 回,他のときはあと $1$ 回の作業を行う必要がある。
$\;\;\;$したがって,$3$ けたの自然数のうち,$3$ 回目の作業で終了するものでは,ア $=$ ウ が成り立つ。
(4)百の位の数が $1$ である $3$ けたの自然数のうち,$3$ 回目の作業で終了するものを求めなさい。
(5)$3$ けたの自然数のうち,$3$ 回目の作業で終了するものは,全部で何個あるかを求めなさい。


