11041中１・素因数分解・素因数分解の利用・最小公倍数

(1) $6$ と $15$ をそれぞれ素因数分解し，下のように素因数をかけます。

$\begin{eqnarray}6&=&2\times3\\[3pt]15&=&3\times 5\end{eqnarray}\;\;$

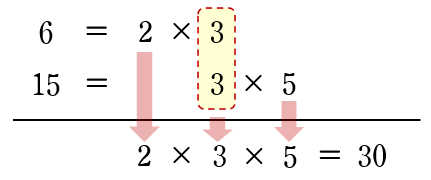
答$30$

(2) $12$ と $18$ をそれぞれ素因数分解し，下のように素因数をかけます。

$\begin{eqnarray}12&=&2^{2}\times3\\[3pt]18&=&2\times 3^{2}\end{eqnarray}\;\;$

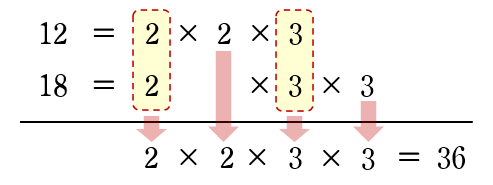
答$36$

(3) $45$ と $70$ をそれぞれ素因数分解し，下のように素因数をかけます。

$\begin{eqnarray}45&=&3^{2}\times5\\[3pt]70&=&2\times 5\times 7\end{eqnarray}\;\;$

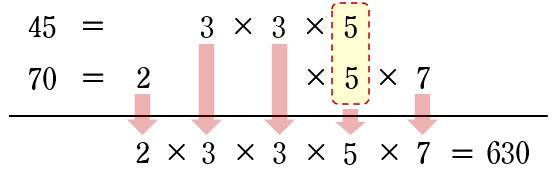
答$630$

(4) $126$ と $198$ をそれぞれ素因数分解し，下のように素因数をかけます。

$\begin{eqnarray}126&=&2\times3^{2}\times7\\[3pt]198&=&2\times 3^{2}\times 11\end{eqnarray}\;\;$

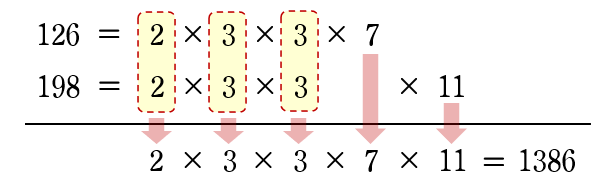
答$1386$

(5) $119$ と $143$ をそれぞれ素因数分解し，下のように素因数をかけます。

$\begin{eqnarray}119&=&7\times17\\[3pt]143&=&11\times 13\end{eqnarray}\;\;$

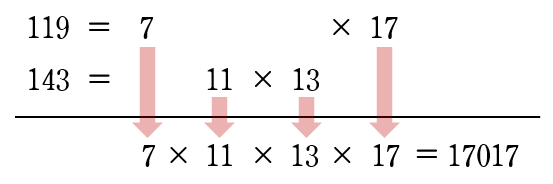
答$17017$