620502中２・三角形と四角形・証明問題 02

2021年11月7日 2024年3月24日

banno

二等辺三角形の頂角の二等分線は，
底辺を垂直に二等分する。

定理：「二等辺三角形の頂角の二等分線は底角を垂直に二等分する」の証明

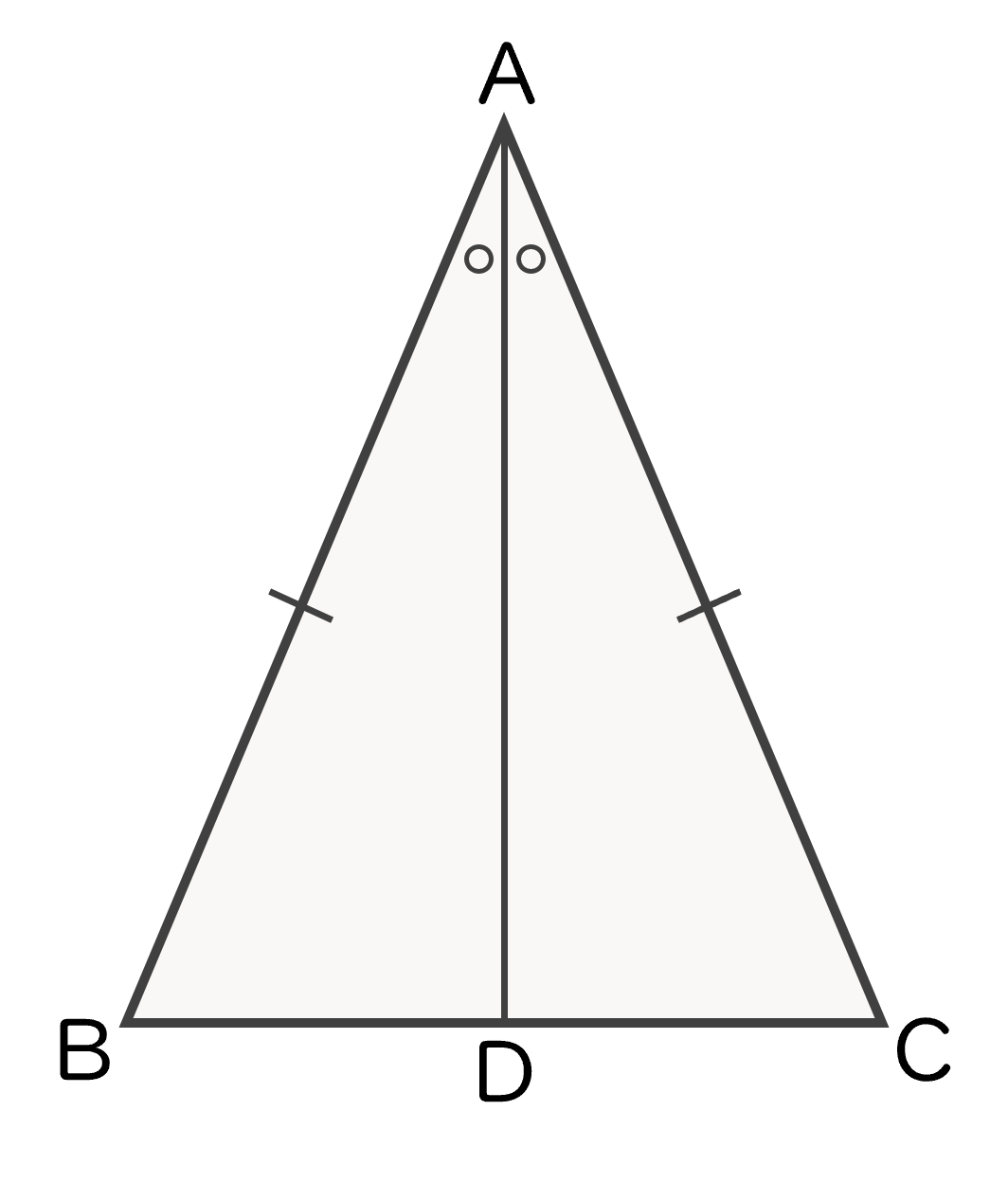
図の△ABC は，AB = AC の二等辺三角形で，
線分 AD は ∠A の二等分線である。
このとき，

線分AD は底辺 BC を垂直に二等分する

ことを証明しなさい。

解答

〈仮定〉AB ＝ AC，∠BAD ＝ ∠CAD
〈結論〉AD ⊥ BC，BD ＝ CD

〈証明〉
△ABD と △ACD で，

仮定から，AB ＝ AC･･････①

AD は頂角 A の二等分線だから，
∠BAD ＝ ∠CAD･･････②

共通な辺だから，AD ＝ AD･･････③

①，②，③から，2 組の辺とその間の角がそれぞれ等しいので
△ABD ≡ △ACD

合同な三角形の対応する辺と角だから
BD ＝ CD･･････④
∠B ＝ ∠C･･････⑤

また，∠ADB ＋ ∠ADC ＝ 180°･･････⑥

⑤，⑥から，∠ADB ＝ 180°×$\frac{\mathsf{1}}{\mathsf{2}}$ ＝ 90°
よって，AD ⊥ BC･･････⑦

④，⑦から，∠A の二等分線 AD は，底辺 BC を垂直に二等分する。