岐阜県・公立高校入試 2021年度( 令和3年度 )解答・解説編
岐阜県立高校・入学試験学力検査・数学・2021年度
1次の(1)~(6)の問いに答えなさい。
(1)$5-3^{2}\;\;$を計算しなさい。
解答・解説
解答$-4$
$5\color{red}-3^{2}$$-3^{2}=-(\,3\times 3\,)=-9$
$=5-9$
$=-4$
(2)$6xy\div \dfrac{2}{\;3\;}x\;\;$を計算しなさい。
解答・解説
解答$9y$
$6xy \div \dfrac{2}{\;3\;}x$
$=6xy \div \dfrac{\;2x\;}{3}$割る数の $\frac{\,2x\,}{3}$ を逆数にしてかけます
$=\color{red}\cancelto{3}{\color{black}6x}\color{black}y \times \dfrac{3}{\;\color{red}\cancel{\color{black}2x}\;}$
$=9y$
(3)$2$ 次方程式$\quad (\,x-3\,)^{2}=9\quad$を解きなさい。
解答・解説
解答$x=0,\; x=6$
$(\,x-3\,)^{2}=9$$(\,x-3\,)$ は $9$ の平方根だと考えます
$x-3=\pm 3$
$x=3\pm 3$
$x=0, \; x=6$
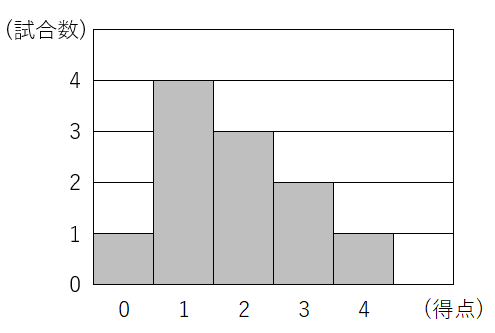
(4)下の図は,あるサッカーチームが,最近の $11$ 試合であげた得点を,ヒストグラムに表したものである。
このヒストグラムについて述べた文として正しいものを,ア ~ エ から $1$ つ選び,符号で書きなさい。
ア中央値と最頻値は等しい。
イ中央値は最頻値より小さい。
ウ中央値と平均値は等しい。
エ中央値は平均値より大きい。
解答・解説
解答エ
下はヒストグラムからつくった度数分布表です。
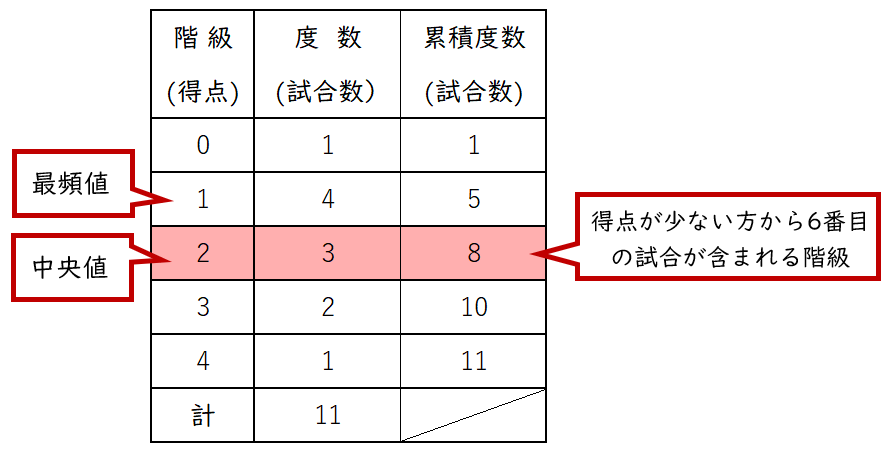
中央値は得点の少ない方から6番目の試合の得点です。
よって,中央値は $2$ 得点
最頻値は最も度数(試合数)が多い得点です。
よって,最頻値は $1$ 得点
平均値は
$(\,0\times 1+1 \times 4+2\times 3+3 \times 2+4 \times1\,)\div11$
$= 20\div 11$
$=1.818\cdots$
これらから,正しいものは エ です。
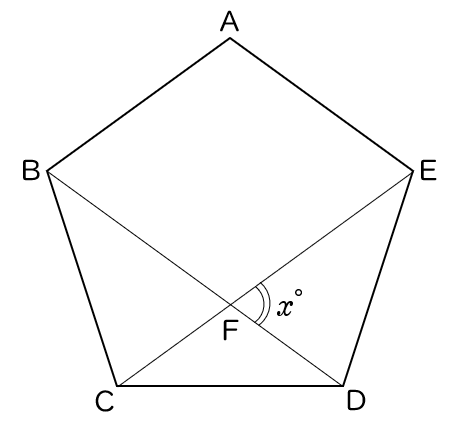
(5)下の図で,五角形 ABCDE は正五角形であり,点 F は対角線 BD と CE の交点である。$x$ の値を求めなさい。
解答・解説
解答$72$
正五角形の内角の和は,
$180°\times (\,5-2\,)=540°$
よって,五角形 ABCDE の $1$ つの内角は,
$540°\div 5=108°$ ・・・ ①
△ CBD は CB $=$ CD の二等辺三角形で,①から ∠BCD $=108°$ だから,
∠BDC $=(\,180°-108°\,)\div 2=36°$
△ DCE についても同様にして,
∠ ECD $=36°$
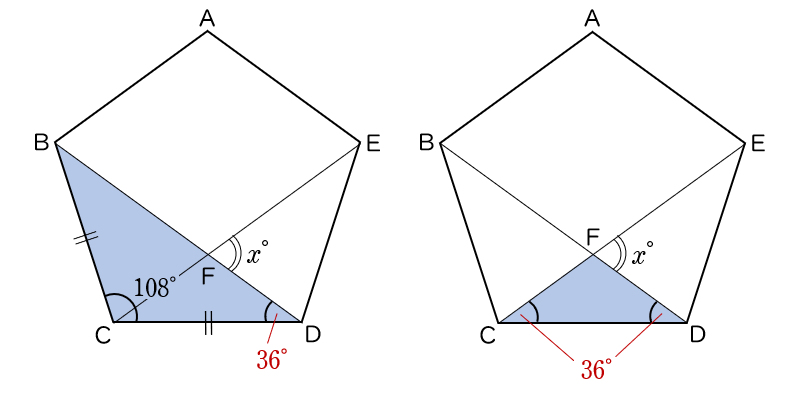
上の図で,△ FCD について,三角形の外角の性質から,
$x°=$ ∠ FCD $+$ ∠FDC $=36°+36°=72°$
よって,$x$ の値は $72$ です。
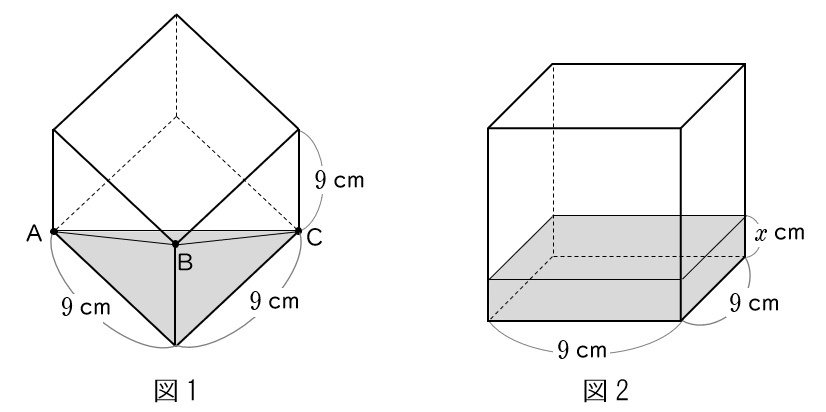
(6)図 1 のように,$1$ 辺の長さが $9$ cmの立方体状の容器に,水面が頂点 A,B,C を通る平面となるように水を入れた。次に,この容器を水平な台の上に置いたところ,図 2 のように,容器の底面から水面までの高さが $x$ cmになった。$x$ の値を求めなさい。
解答・解説
解答$\dfrac{3}{\;2\;}$ ( $1.5$ )
図 1 の水の体積を求めます。
求める体積は,下の図で,△ ACD が底辺,辺 BD が高さである三角錐の体積です。
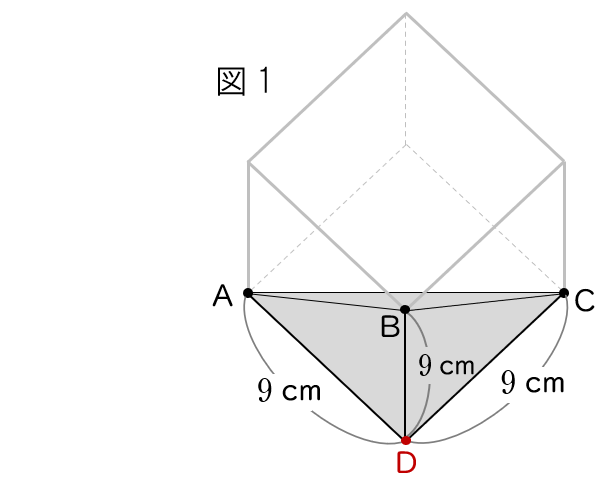
水の体積(cm$^{3}$) $=$ △ ACD の面積 × BD × $\dfrac{1}{\;3\;}$
$= \biggl(9\times9\times\dfrac{1}{\;2\;}\biggr)\times 9 \times\dfrac{1}{\;3\;}$
$=\dfrac{\;81\;}{2}\times 9 \times\dfrac{1}{\;3\;}$
$=\dfrac{\;243\;}{2}$
これが図 2 の水の体積と同じなので,
$9\times9\times x=\dfrac{\;243\;}{2}$
$x=\dfrac{\;3\;}{2}$
2電子レンジで食品 A を調理するとき,電子レンジの出力を $x$ W,食品 A の調理にかかる時間を $y$ 分とすると,$y$ は $x$ に反比例する。電子レンジの出力が $500$ W のとき,食品 A の調理にかかる時間は $8$ 分である。
次の (1),(2) の問いに答えなさい。
(1)$y$ を $x$ の式で表しなさい。
解答・解説
解答$y=\dfrac{\,4000\,}{x}$
$y$ は $x$ に反比例するので,比例定数を $a$ とすると,求める式は,
$y=\dfrac{a}{\;x\;}$
と表すことができます。
問題文から,$x=500$ のとき $y=8$ だから,
$y=\dfrac{a}{\;x\;}$ に $x=500$ のとき $y=8$ を代入して,
$8=\dfrac{a}{\;500\;}$
$a=4000$
よって,求める式は,
$y=\dfrac{\,4000\,}{x}$
(2)電子レンジの出力が $600$ W のとき,食品 A の調理にかかる時間は,何分何秒であるかを求めなさい。
解答・解説
解答$6$ 分 $40$ 秒
$y=\dfrac{\,4000\,}{x}$ に $x=600$ を代入して,
$y=\dfrac{\,4000\,}{600}=\dfrac{\,20\,}{3}$
$\dfrac{\,20\,}{3}\,$(分) $=$ $\;6\dfrac{\,2\,}{3}\,$(分) $=6$ 分 $40$ 秒$\dfrac{2}{\,3\,}$分$\;=60\times \dfrac{2}{\,3\,}=40$秒
3赤と白の $2$ 個のさいころを同時に投げる。このとき,赤いさいころの出た目の数を $a$ ,白いさいころの出た目の数を $b$ として,座標平面上に,直線 $y=ax+b$ をつくる。
例えば,$a=2$ ,$b=3$ のときは,座標平面上に,直線 $y=2x+3$ ができる。
次の (1) ~ (3) の問いに答えなさい。
(1)つくることができる直線は全部で何通りあるかを求めなさい。
解答・解説
解答$36$ 通り
$2$ 個のさいころの目の出方は $6\times6=36$ (通り) です。
そのすべての場合の $a$ と $b$ の組み合わせを下の図に表します。
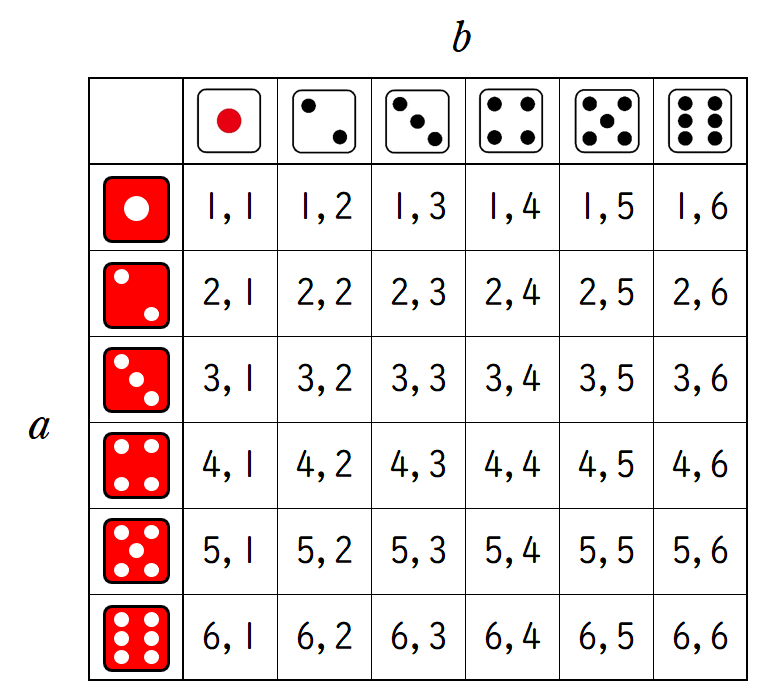
この $36$ 通りについて,つくることのできる直線はすべて異なります。
よって,つくることのできる直線は全部で $36$ 通りあります。
(2)傾きが $1$ の直線ができる確率を求めなさい。
解答・解説
解答$\dfrac{1}{\;6\;}$
傾きが $1$ の直線ができるのは,$a=1$ のときです。
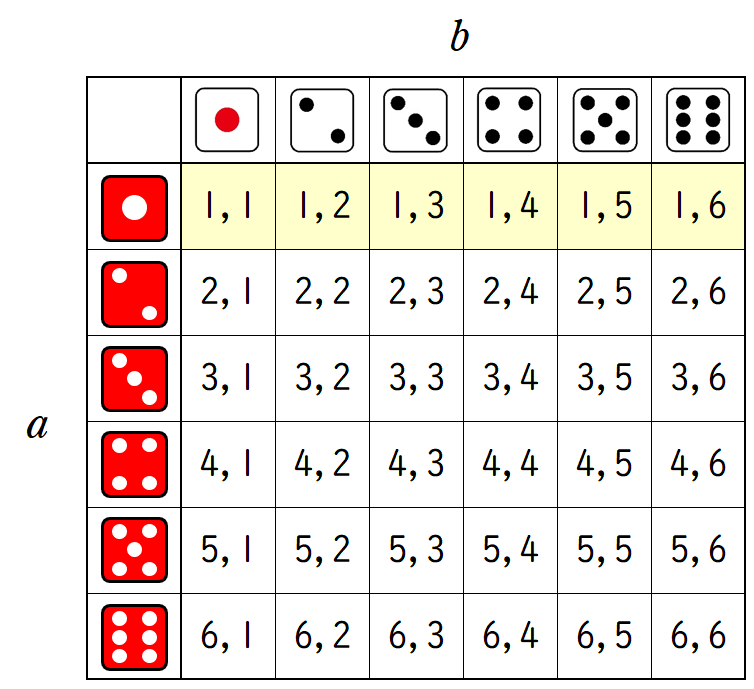
上の図から,$a=1$ である場合は $6$ 通りあります。
よって,傾きが $1$ である直線ができる確率は,
$\dfrac{6}{\;36\;}=\dfrac{1}{\;6\;}$
(3)$3$ 直線 $y=x+2$,$y=-x+2$,$y=ax+b$ で三角形ができない確率を求めなさい。
解答・解説
解答$\dfrac{11}{\;36\;}$
直線 $y=x+2$,$y=-x+2$ は,下の図のようになります。
$y=x+2$ … ①,$y=-x+2$ … ② とします。
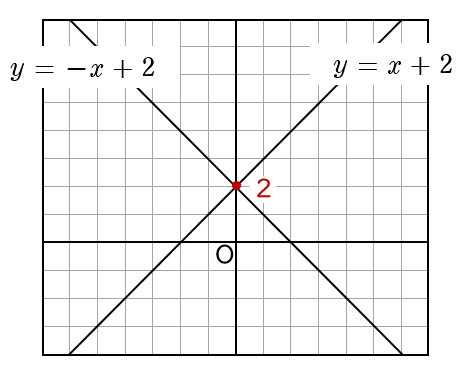
ここに $y=ax+b$ を引いて,三角形ができないときは以下の $2$ 通りの場合です。
〔1〕$y=ax+b$ が ①,② のどちらかと平行になるとき
〔2〕$3$ 直線 ①,②,$y=ax+b$ が $1$ 点で交わるとき
この $2$ 通りについて調べます。
〔1〕$y=ax+b$ が ①,② のどちらとも平行になるとき
$y=ax+b$ が ① と平行になるときは,
$y=ax+b$ と ① の傾きが同じとき,
つまり,$a=1$ のときです。
この場合は (1) から $6$ 通りです。
また,$a$ は $1$ から $6$ までの整数だから,
$y=ax+b$ が ② と平行になるときはありません。
〔2〕$3$ 直線 ①,②,$y=ax+b$ が $1$ 点で交わるとき
①,②,$y=ax+b$ が $1$ 点で交わるときは,
上のグラフから, $y=ax+b$ が $(\,0,\;2\,)$ を通るとき,
つまり,$b=2$ のときであることが分かります。
この場合は下の図から $6$ 通りあることが分かります。
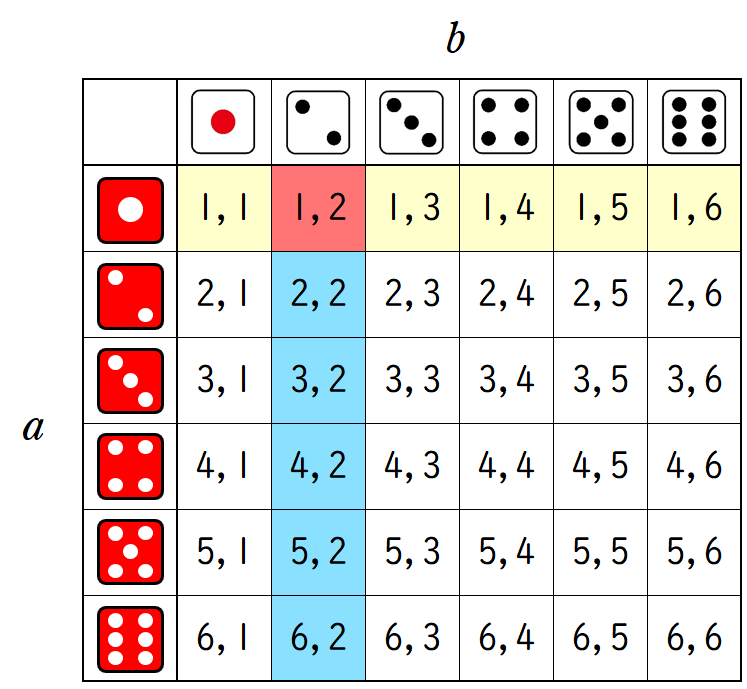
これらのことから,〔1〕と〔2〕の場合はそれぞれ $6$ 通りずつあり,
また,$a=1$,$b=2$ の場合は 〔1〕と〔2〕のどちらにも含まれるので,
$3$ 直線で三角形ができない場合の数は,
$6+6-1=11$ (通り)
よって,$3$ 直線で三角形ができない確率は,
$\dfrac{11}{\;36\;}$
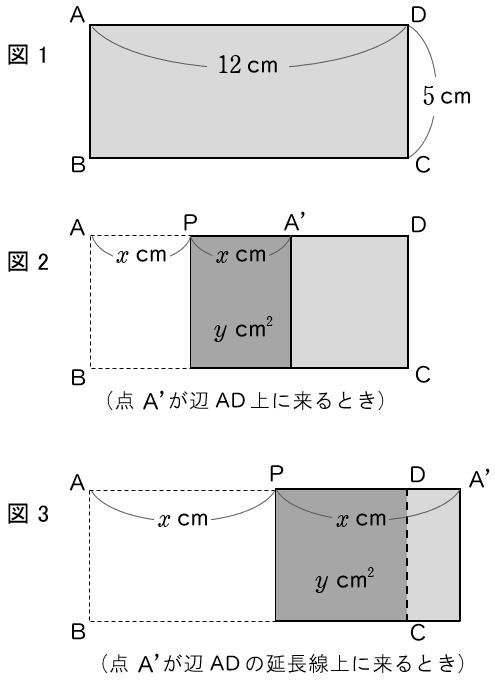
4図 1 のような,縦 $5$ cm,横 $12$ cm の長方形 ABCD のセロハンがある。
辺 AD 上に点 P をとり,点 A が直線 AD 上の点 A’ にくるようにセロハンを点 P で折り返すと,図 2 や図 3 のように,セロハンが重なった部分の色が濃くなった。
AP の長さを $x$ cm,セロハンが重なって色が濃くなった部分の面積を $y$ cm$^{2}$ とする。
次の (1) ~ (4) の問いに答えなさい。
(1)表中の ア ,イ に当てはまる数を求めなさい。

(2)$x$ の変域を次の (ア),(イ) とするとき,$y$ を $x$ の式で表しなさい。
(ア)$0≦x≦6$ のとき
(イ)$6≦x≦12$ のとき
(1) の 解答・解説
解答ア $30$ イ $20$
$x=6$ のとき,下の図のようになります。
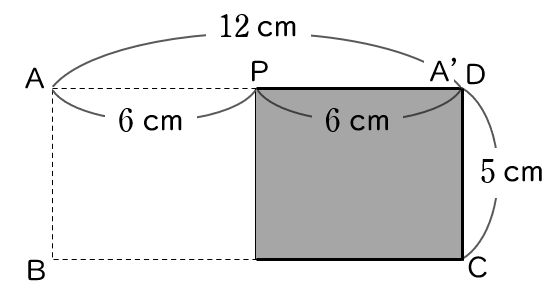
このとき,
$y=6\times 5 = 30$ア30
$x=8$ のとき,下の図のようになります。
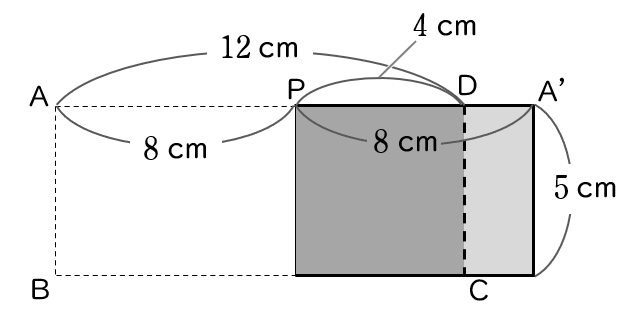
このとき,
$y=4\times 5 = 20$イ20
(2) の 解答・解説
解答(ア) $y=5x\quad$(イ) $y=-5x+60$
$0≦x≦12$ において,$y$ は一定の割合で増減するから,
$0≦x≦12$ において,$y$ は $x$ の1 次関数です。
(ア)$0≦x≦6$ のとき
(1) から,$x$ と $y$ の変化の様子は次の表のようになります。
$\begin{array}{c|ccc}\;\;x &\; 0 & \cdots & 6\;\, \\ \hline \;\;y & \;0 & \cdots & 30\; \ \end{array}$
$x$ と $y$ の関係を表す式を $y=ax+b$ と表すと,
$a=\dfrac{\;30-0\;}{\;6-0}=\dfrac{\;30\;}{6}=5$
よって,求める式は $y=5x+b$ となり,
さらに,この式に $x=0$,$y=0$ を代入して,
$0=5\times 0 +b$
$b=0$
したがって,求める式は式 $y=5x$ $\;(\,0≦x≦6\,) $
※ 実際には $y$ が $x$ に比例していることは明らかなので,
求める式を $y=ax$ とし,$x=6$,$y=30$ を代入して $a$ を求めればよいでしょう。
(イ)$6≦x≦12$ のとき
(1) から,$x$ と $y$ の変化の様子は次の表のようになります。
$\begin{array}{c|ccc}\;\;x &\; 6 & \cdots & 12\;\, \\ \hline \;\;y & \;30 & \cdots & 0\; \ \end{array}$
$x$ と $y$ の関係を表す式を $y=ax+b$ と表すと,
$a=\dfrac{\;\;0-30\;}{12-6}=\dfrac{\;-30\;}{6}=-5$
よって,求める式は $y=-5x+b$ となり,
さらに,この式に $x=12$,$y=0$ を代入して,
$0=-5\times 12 +b$
$b=60$
したがって,求める式は式 $y=-5x+60$ $\;(\,6≦x≦12\,) $
(3)$x$ と $y$ の関係を表すグラフを書きなさい。( $0≦x≦12$ )
解答・解説
解答
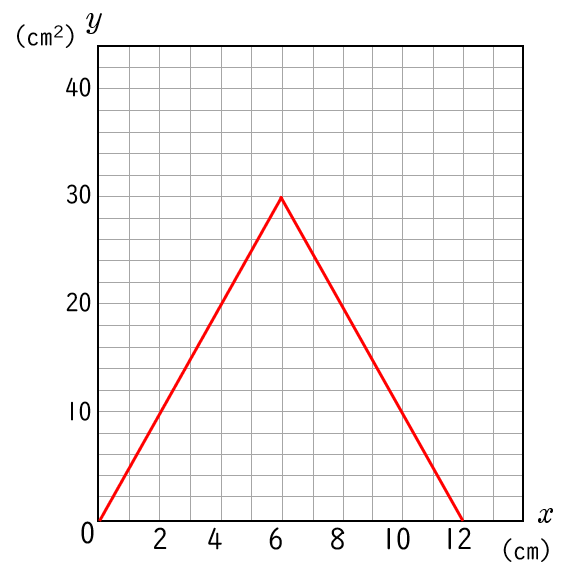
解説
$0≦x≦12$ において,$y$ は $x$ の1 次関数だから,
$0≦x≦12$ の範囲のグラフは直線になります。
(1) から,$x$ と $y$ の関係は下の表のようになります。
$\begin{array}{c|ccccc}\;\;x &\; 0 & \cdots & 6 & \cdots & 12 \;\, \\ \hline \;\;y & \;0 & \cdots & 30 & \cdots & 0 \; \ \end{array}$
よって,座標 $(\,0,\;0\,)$,$(\,6,\;30\,)$, $(\,12,\;0\,)$ を順に直線で結びます。
(4)セロハンが重なって色が濃くなった部分の面積が,重なっていないセロハンの部分の面積の $2$ 倍になるときがある。このときの AP の長さのうち,最も長いものは何cmであるかを求めなさい。
解答・解説
解答$\dfrac{\;36\;}{5}$ cm $\quad$($\;7.2\,$cm )
セロハンが重なって色が濃くなった部分の面積が,
重なっていないセロハンの部分の面積の $2$ 倍になるときは,
図 4 :点 A' が辺 AD 上にあるときに $1$ 回,
図 5 :点 A' が辺 AD の延長線上にあるときに $1$ 回,
あります。
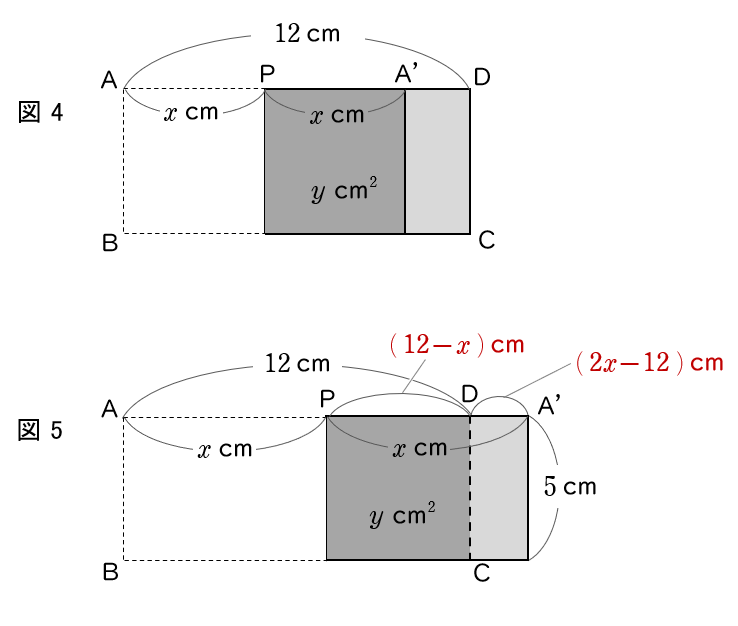
AP の長さ ( $=x$ ) が最も長いのは,図 5 のようになるときです。
このときの $x$ について方程式をつくります。
重なった部分の面積 ($y$) $=$ 重なっていない部分の面積の $2$ 倍
$5(\,12-x\,)=5(\,2x-12\,)\times 2$
$12-x=4x-24$
$x=\dfrac{\;36\;}{5}$
5下の図で,$4$ 点 A,B,C,D は円 O の周上の点であり,△ ABC は正三角形である。
また,点 E は線分 BD 上の点で,BE $=$ CD である。
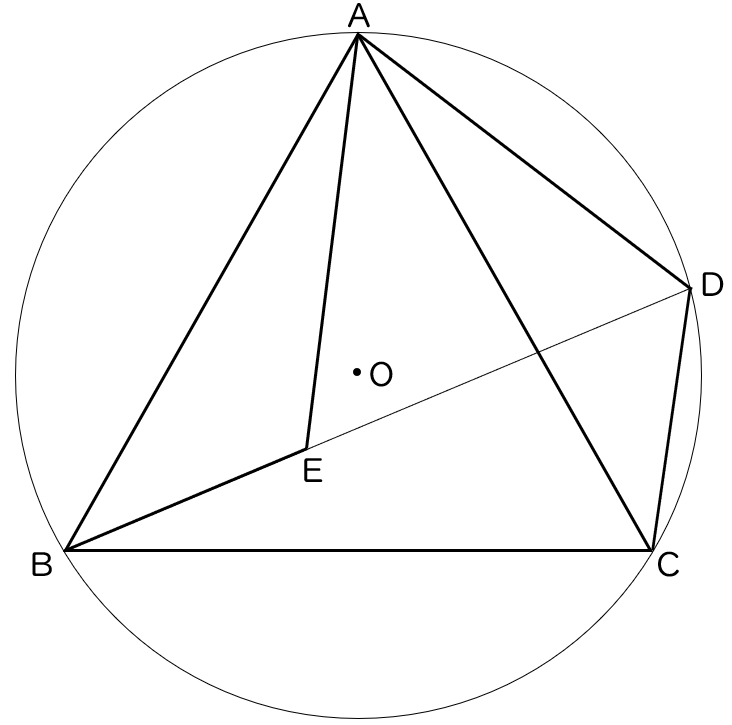
次の (1),(2) の問いに答えなさい。
(1)AE $=$ AD であることを証明しなさい。
解答
〈仮定〉$4$ 点 A,B,C,D は円 O の周上の点,
△ ABC は正三角形,BE $=$ CD
〈結論〉AE $=$ AD
〈証明〉
△ABE と △ACD で,
仮定から,AB = AC・・・・・・①
仮定から,BE = CD・・・・・・②
$\small\stackrel{\huge\frown}{\sf AD}$ に対する円周角だから,
∠ABE = ∠ACD・・・・・・③
①,②,③ から,$2$ 組の辺とその間の角がそれぞれ等しいので,
△ABE ≡ △ACD
合同な三角形の対応する辺だから,
AE = AD
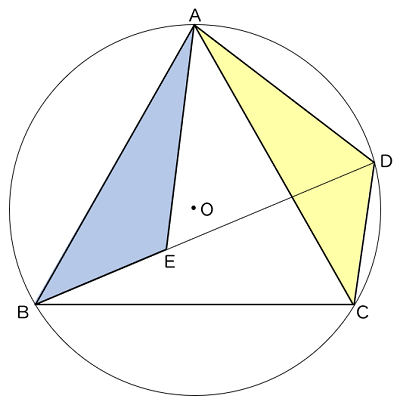
(2)点 A から線分 BD にひいた垂線と BD との交点を H とする。
AB $=6$ cm,∠ABD $=45$° のとき,
(ア)AH の長さを求めなさい。
解答・解説
解答$3\sqrt{\,2\,}$ cm
仮定から∠AHB $=90°$,∠ABD $=45°$ だから,
∠BAH $=180°-(\,90°+45°\,)=45°$
よって,△ ABC は ∠AHB $=90°$ の直角二等辺三角形です (下の図) 。
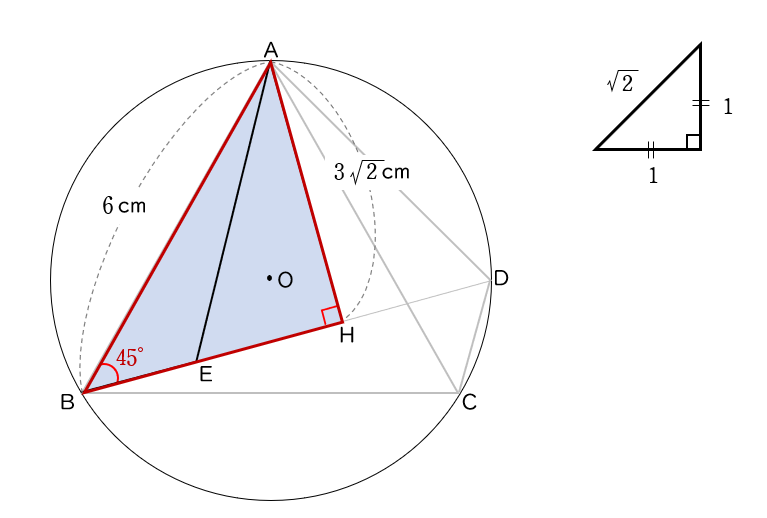
よって,
AH:BH :AB $=$ $1$:$1$:$\sqrt{\,2\,}$
AH:AB $=$ $1$:$\sqrt{\,2\,}$
AH:6 $=$ $1$:$\sqrt{\,2\,}$
AH$\times \sqrt{\,2\,}$ $=$ $6\times 1$
AH $=$ $6\div \sqrt{\,2\,}$$\small 6\div\sqrt{2}=\dfrac{6}{\sqrt{2}}=\dfrac{6\;\,\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}=\dfrac{6\sqrt{2}}{2}=3\sqrt{2}$
$=3\sqrt{\,2\,}$ (cm)
(イ)△ ABE の面積を求めなさい。
解答・解説
解答$9-3\sqrt{\,3\,}$ (cm)
△ ABE を 底辺が BE,高さが AH である三角形と考えます。
そこで,BE を BH と EH の差として求めます。
仮定から,△ABC は正三角形だから,∠ACB $=60°$ ・・・ ①
$\small\stackrel{\huge\frown}{\sf AB}$ に対する円周角だから,∠ACB = ∠ADE ・・・ ②
①,② から,∠ADE $=60°$ ・・・ ③
また,(1) から,AE $=$ AD
よって,△AED は AE $=$ AD の二等辺三角形
したがって,∠ADE $=$ ∠AED ・・・ ④
③,④ から,∠AEH $=60°$
さらに,仮定から ∠AHE $=90°$ だから,
△AEH は $3$ つの角が $90°$,$60°$,$30°$ の直角三角形です (下の図) 。
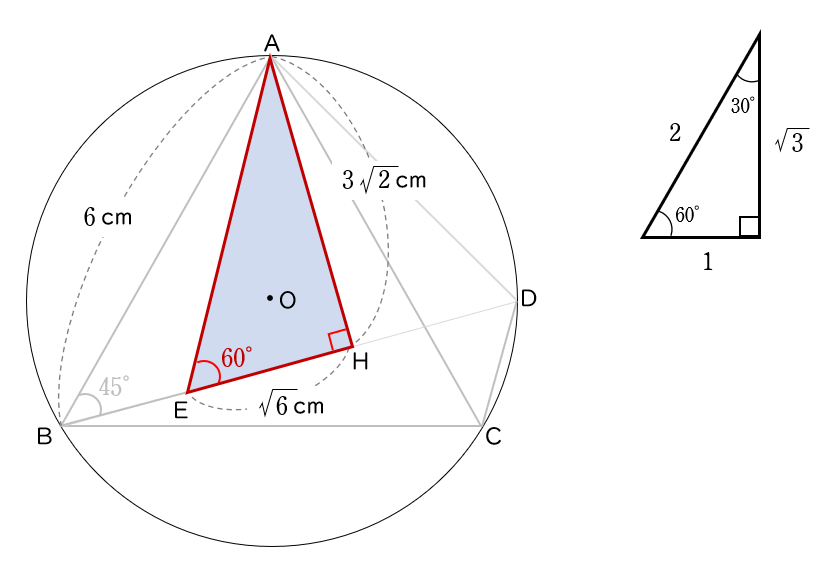
(ア) から,AH $=3\sqrt{\,2\,}$ (cm) だから,
EH:AH :AE $=$ $1$:$\sqrt{\,3\,}$:$2$
EH:AH $=$ $1$:$\sqrt{\,3\,}$
EH:$3\sqrt{\,2\,}$ $=$ $1$:$\sqrt{\,3\,}$
EH$\times \sqrt{\,3\,}$ $=$ $3\sqrt{\,2\,}\times 1$
EH $=$ $3\sqrt{\,2\,}\div \sqrt{\,3\,}$$\small 3\sqrt{\,2\,}\div\sqrt{3}=\dfrac{3\sqrt{2}}{\sqrt{3}}=\dfrac{3\sqrt{2}\times\sqrt{3}}{\sqrt{3}\;\times\sqrt{3}}=\dfrac{3\sqrt{6}}{3}=\sqrt{6}$
$=\sqrt{\,6\,}$ (cm)
また,(ア) から △ABH は AH $=$ BH の直角二等辺三角形だから,
BH $= 3\sqrt{\,2\,}$ (cm)
よって,
BE $=3\sqrt{\,2\,}-\sqrt{\,6\,}$ (cm)
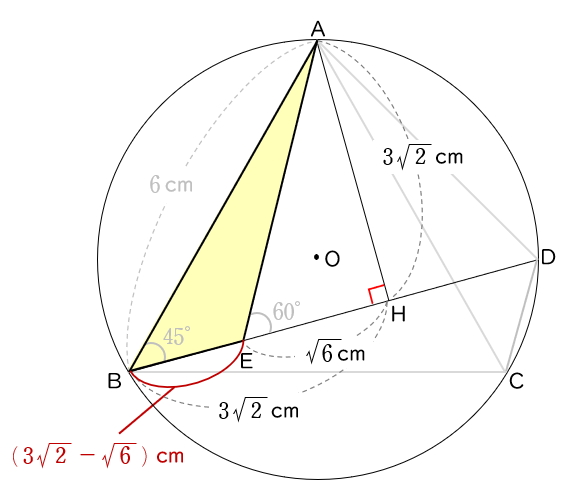
△ABE の面積は,
BE $\times$ AH $\times \dfrac{1}{\;2\;}$
$=(\,3\sqrt{\,2\,}-\sqrt{\,6\,}\,)\times 3\sqrt{\,2\,}\times \dfrac{1}{\;2\;}$
$=(\,18-6\sqrt{\,3\,}\,)\times \dfrac{1}{\;2\;}$
$=9-3\sqrt{\,3\,}$ (cm)
6$150$ 枚のカードがある。これらのカードは下の図のように,表には,$1$ から $150$ までの自然数が $1$ つずつ書いてあり,裏には,表の数の,正の平方根の整数部分が書いてある。
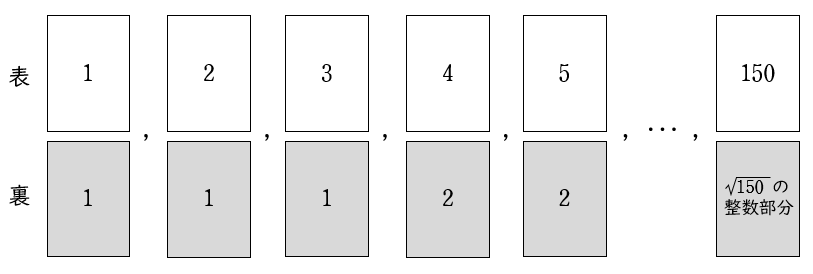
次の (1) ~ (4) の問いに答えなさい。
(1)表の数が $10$ であるカードの裏の数を求めなさい。
解答・解説
解答$3$
表の数が $10$ であるカードの裏の数は,$\sqrt{\,10\,}$ の整数部分です。
$\sqrt{\,9\,}≦\sqrt{\,10\,}≦\sqrt{\,16\,}$
$3≦\sqrt{\,10\,}≦4$
よって,$\sqrt{\,10\,}$ の整数部分は $3$ です。
(2)次の文章は,裏の数が $n$ であるカードの枚数について,花子さんが考えたことをまとめたものである。
ア,イ には数を,ウ ~ オ には $n$ を使った式を,それぞれあてはまるように書きなさい。
表の数が $150$ であるカードの裏の数は ア であるので,裏の数 $n$ は ア 以下の自然数になる。
(Ⅰ) $\,\; n$ が ア のとき
裏の数が ア であるカードは,全部で イ 枚ある。
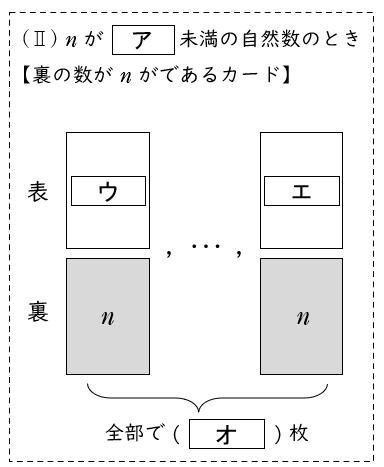
(Ⅱ) $\,\; n$ が ア 未満の自然数のとき
裏の数が $n$ であるカードのうち,最も小さい数は ウ であり,最も大きい数は エ である。
よって,裏の数が $n$ であるカードは,全部で ( オ ) 枚ある。
解答・解説
解答ア$\;\;12$,$\quad$イ$\;\;7$,$\quad$ウ$\;\;n^{2}$,$\quad$エ$\;\;n^{2}+2n$,$\quad$オ$\;\;2n+1$
表の数が $150$ であるカードの裏の数は,$\sqrt{\,150\,}$ の整数部分です。
$\sqrt{\,144\,}≦\sqrt{\,150\,}≦\sqrt{\,169\,}$
$12≦\sqrt{\,150\,}≦13$
よって,$\sqrt{\,150\,}$ の整数部分は $12$ だから,
表の数が $150$ であるカードの裏の数は $12$ です。 ア12
$150$ は表の最大の数だから,裏の最大の数は $12$ ,
つまり,裏の数 $n$ は $12$ 以下の自然数になります。
(Ⅰ) $n$ が $12$ のとき
表の最小の数は,正の平方根が $12$ になる最小の数,
つまり,$12^{2}=144$ です。
よって,裏の数が $12$ であるカードは,
表の数が $144$ から $150$ までのカードで,
その枚数は,$150-144\color{red}+1\color{black}=7$ (枚) イ7
(Ⅰ) $n$ が $12$ 未満の自然数のとき
表の最小の数は,正の平方根が $n$ になる最小の数,
つまり,$n^{2}$ です。 ウ$n^{2}$
表の最大の数は,正の平方根が $n+1$ になる最小の数より $1$ 小さい数,
つまり,$(\,n+1\,)^{2}-1=n^{2}+2n$ です。 エ$n^{2}+2n$
よって,裏の数が $n$ であるカードは,
表の数が $n^{2}$ から $(\,n^{2}+2n\,)$ までのカードで,
その枚数は,$(\,n^{2}+2n\,)-n^{2}\color{red}+1\color{black}=2n+1$ (枚) オ$2n+1$
(3)裏の数が $9$ であるカードは全部で何枚あるかを求めなさい。
解答・解説
解答$19$ 枚
(2) から,$n<12$ のとき,
裏の数が $n$ であるカードの枚数は $(\,2n+1\,)$ 枚 だから,
$n=9$ であるカードの枚数は,
$2\times 9+1=19$ (枚)
(4)$150$ 枚のカードの裏の数を全てかけ合わせた数を $P$ とする。$P$ を $3^{m}$ で割った数が整数になるとき,$m$ に当てはまる自然数のうちで最も大きい数を求めなさい。
解答・解説
解答$65$
まず,実際に $P$ を裏の数の累乗の積の形の式で表してみます。
( 各カードの枚数は下の参考で求めています )
$\small P=1 ^{3} \times2 ^{5} \times 3 ^{7} \times 4 ^{9} \times 5 ^{11} \times 6 ^{13} \times 7 ^{15} \times 8 ^{17} \times 9^{19} \times 10^{21} \times 11^{23} \times 12^{7}$
この $P$ を $3^{m}$ で割り切るので,$P$ の素因数 $3$ の指数を求めます。
上の式の因数で,素因数分解したときに $3$ の累乗をふくむものは,
$3 ^{7}$,$6 ^{13}$,$9^{19}$,$12^{7}$
です。これらをそれぞれ素因数分解すると,
$\color{red}3 ^{7}$
$6 ^{13}=(\,2\times3\,)^{13}=2^{13}\times \color{red}3^{13}$
$9^{19}=(\,3^{2}\,)^{19}=\color{red}3^{38}$
$12^{7}=(\,2^{2}\times3\,)^{7}=2^{14}\times \color{red}3^{7} $
さらにこれらをかけ合わせると,
$3 ^{7}\times (\,2^{13}\times3^{13}\,)\times 3^{38}\times (\,2^{14}\times 3^{7}\,)=2 ^{27}\times \color{red}3^{65}$
よって,$P$ の素因数 $3$ の指数は $65$ です。
つまり,$P$ を $3^{m}$ で割った数が整数になるのは,
$m$ が $65$ 以下の自然数になるときであることが分かりました。
したがって,$m$ に当てはまる最大の自然数は,$65$ です。
参 考
カードの裏の数別の枚数は以下の表になります。
裏が $n$ であるカードは $2n+1$ (枚) なので,
裏の数が $3$ から $11$ までのカードの枚数は, $3$ から始まる奇数です。
| 裏の数 | 枚数を求める式 | 枚数 (枚) |
|---|---|---|
| $1$ | $2\times 1+1$ | 3 |
| $2$ | $2\times 2+1$ | 5 |
| $3$ | $2\times 3+1$ | 7 |
| $4$ | $2\times 4+1$ | 9 |
| $5$ | $2\times 5+1$ | 11 |
| $6$ | $2\times 6+1$ | 13 |
| $7$ | $2\times 7+1$ | 15 |
| $8$ | $2\times 8+1$ | 17 |
| $9$ | $2\times 9+1$ | 19 |
| $10$ | $2\times 10+1$ | 21 |
| $11$ | $2\times 11+1$ | 23 |
| $12$ | (2) から | 7 |
上の解説では,はじめに $P$ を全ての裏の数の累乗の積の形にしていますが,
$P$ の因数で $3$ を含むものは,裏の数が $3$ の倍数であることは明らかなので,
はじめから,裏の数が $3$,$6$,$9$,$12$ の場合だけを考えればよいでしょう。

