岐阜県・公立高校入試 2018年度( 平成30年度 )解答・解説編
岐阜県立高校・入学試験学力検査・数学・2018年度
1次の(1)~(6)の問いに答えなさい。
(1)$9-6\times 2\;\;$を計算しなさい。
解答・解説
解答$-3$
$9\;\color{red}{-\;6\times 2}$まず乗法から計算します
$=9-12$
$=-3$
(2)$12ab\div\dfrac{\;3\;}{4}b\;\;$を計算しなさい。
解答・解説
解答$16a$
$12ab\div\dfrac{\;3\;}{4}b$
$=\color{red}\cancel{\color{black}18}\color{black}a\color{red}\cancel{\color{black}b}\;\color{red}{\times\;\dfrac{4}{\cancel{3b}}}$
$\dfrac{3}{\;4\;}b\;$を逆数にしてかけます
$=4a\times 4$
$=16a$
(3)$(\;\sqrt{\,3\,}-\sqrt{\,2\,}\;)^{2}\;\;$を計算しなさい。
解答・解説
解答$5-2\sqrt{\,6\,}$
$(\;\sqrt{\,3\,}-\sqrt{2}\;)^{2}$
$=(\;\sqrt{\,3\,}\;)^{2}-2\sqrt{\,3\,}\sqrt{\,2\,}+(\;\sqrt{\,2\,}\;)^{2}$
$=3-2\sqrt{\,6\,}+2$
$=5-2\sqrt{\,6\,}$
(4)$y$ が $x$ に反比例し,$x=4$ のとき $y=3$ である。$x$ と $y$ の関係を式で表しなさい。
解答・解説
解答$y=\dfrac{\;12\;}{x}$
$y$ は $x$ に反比例するから,比例定数を $a$ とすると,
求める式は $y=\dfrac{a}{\;x\;}$ と表される。
この式に $x=4$,$y=3$ を代入して,
$3=\dfrac{a}{\;4\;}$
$a=12$
よって,$y=\dfrac{\;12\;}{x}$
(5)下の図で,$4$ 点 A,B,C,D は円 O の周上にあり,AC は 円 O の直径である。∠CAD $=72°$ のとき,$x$ の値を求めなさい。
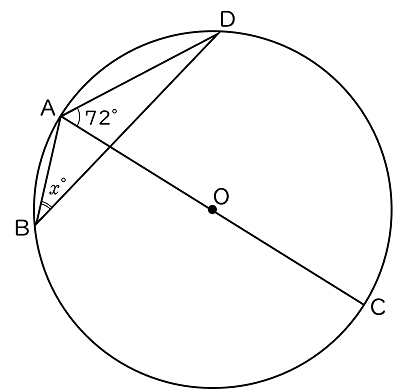
解答・解説
解答$18°$
下の図のように線分 BC をかきます。
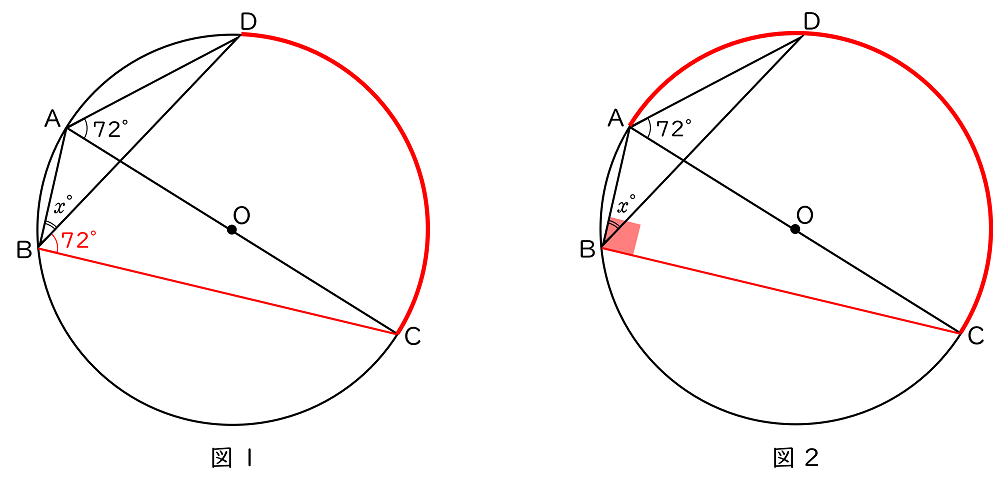
$\sf\stackrel{\huge\frown}{CD}$ に対する円周角だから(図 1),
∠CBD $=$ ∠DAC $=72°$
また,線分 AC は円 O の直径で,半円の弧に対する円周角だから(図 2),
∠ABC $=90°$
よって,$x=$ ∠ABC - ∠CBD
$=90-72$
$=18$ (°)
(6)$2$ 個のさいころを同時に投げとき,出る目の数の和が $5$ の倍数になる確率を求めなさい。
解答・解説
解答$\dfrac{7}{36}$
$2$ 個のさいころの目の出方は $6 \times 6=36$(通り)です。
そのすべての場合について,$2$ 個のさいころの出る目の数の和を下の表に示します。
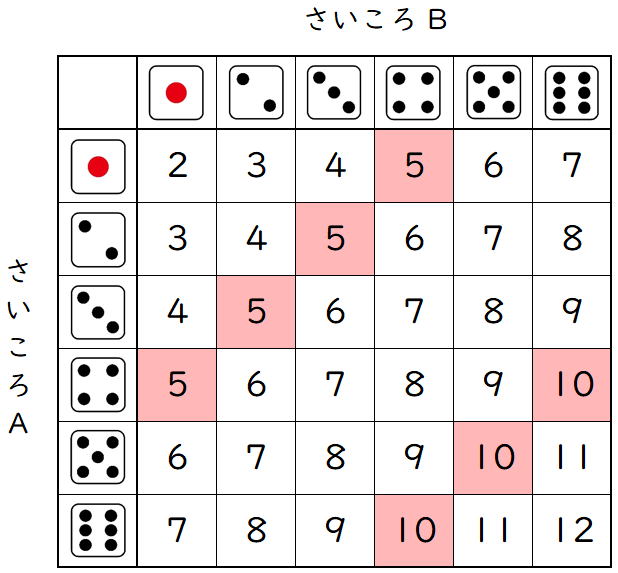
表から, 出る目の数の和が $5$ になる場合は $4$ 通り,
出る目の数の和が $10$ になる場合は $3$ 通りあります。
よって,求める確率は,$\dfrac{\;4+3\;}{36}=\dfrac{7}{\;36\;}$
2ある中学校で読書週間中に,それぞれの生徒が読んだ本の冊数を調べた。右の図は,$1$ 年 $1$ 組の結果をヒストグラムに表したものである。ただし,$1$ 年 $1$ 組の生徒で読んだ本が $8$ 冊以上の生徒はいない。
次の (1) ~ (3) の問いに答えなさい。
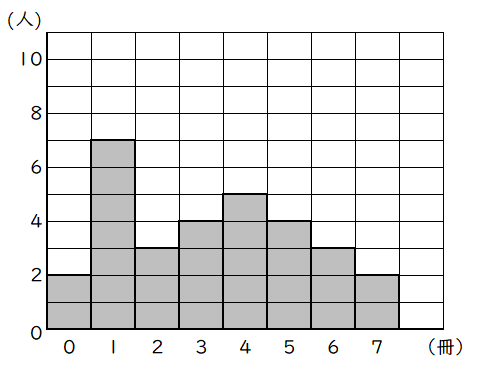
(1)$1$ 年 $1$ 組の生徒の総数は何人であるかを求めなさい。
解答・解説
解答$30$ 人
ヒストグラムを度数分布表にします。
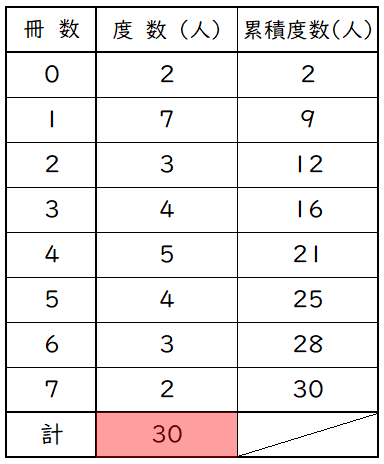
求める人数は,表の度数の合計です。
$2+7+3+4+5+4+3+2=30$(人)
(2)$1$ 年 $1$ 組のそれぞれの生徒が読んだ本の冊数の中央値を求めなさい。
解答・解説
解答$3$ 冊
ヒストグラムを度数分布表にします。
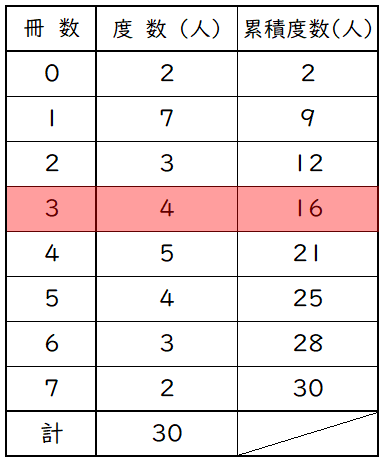
(1) から,人数の合計は $30$ 人なので,
中央値は冊数の少ない方から $15$ 人目と $16$人目の平均になります。
表の累積度数から,$2$ 冊までが $12$ 人,$3$ 冊までが $16$ 人なので,
少ない方から $15$ 人目と $16$ 人目はともに $3$ 冊の階級になります。
よって,中央値は,$\dfrac{\;3+3\;}{2}=3$(冊)です。
(3)この中学校の生徒の総数は $200$ 人である。この中学校の生徒で読んだ本が $3$ 冊以上の生徒の相対度数と $1$ 年 $1$ 組の生徒で読んだ本が $3$ 冊上の生徒の相対度数は,同じ値であった。この中学校の生徒で読んだ本が $3$ 冊上の生徒は何人であるかを求めなさい。
解答・解説
解答$120$ 人
ヒストグラムを度数分布表にします。
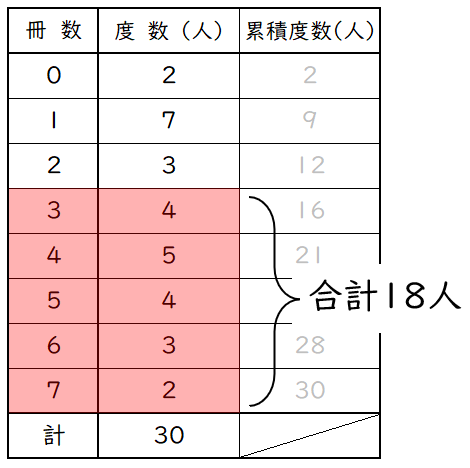
表から,$1$ 年 $1$ 組の生徒で $3$ 冊以上読んだ生徒の合計は $18$ 人なので,
その相対度数は,$\dfrac{18}{\;30\;}=0.6\;$です。
これが,この中学校全体の $3$ 冊以上読んだ生徒の相対度数と等しいので,
この中学校の生徒で読んだ本が $3$ 冊上の生徒数は,
$200\times 0.6=120$(人)
3商品 A は,$1$ 個 $120$ 円で売ると $1$ 日あたり $240$ 個売れ,$1$ 円値下げするごとに $1$ 日あたり $4$ 個多く売れるものとする。
次の (1)~(3) の問いに答えなさい。
(1)$1$ 個 $110$ 円で売るとき, $1$ 日で売れる金額の合計はいくらになるかを求めなさい。
解答・解説
解答$30800$ 円
$1$ 個 $120$ 円で売ると $1$ 日あたり $240$ 個売れます。
$1$ 個 $110$ 円で売るとき,値下げした金額は,$120-110=10$(円)です。
$1$ 円値下げするごとに $4$ 個多く売れるから,
$10$ 円値下げすると,$4\times 10=40$(個)多く売れます。
つまり,$1$ 個 $110$ 円では $(\;240+40\;)$ 個売れることになります。
よって,$1$ 日で売れる金額の合計は, $110\times(\;240+40\;)=30800$(円)
(2)$x$ 円値下げするとき,$1$ 日あたり何個売れるかを,$x$ を使った式で表しなさい。
解答・解説
解答$4x+240$(個)
$1$ 円値下げするごとに $4$ 個多く売れるから,
$x$ 円値下げすると,$4\times x=40x$(個)多く売れます。
よって,$40x+240$(個)売れます。
(3)$1$ 個 $120$ 円で売るときよりも,$1$ 日で売れる金額の合計を $3600$ 円増やすためには,$1$ 個何円で売るとよいかを求めなさい。
解答・解説
解答$90$(円)
$x$ 円値下げするとします。
その場合,(2)から売れる個数は,$4x+240$(個)なので,
$1$ 日で売れる金額の合計は,
$(\;120-x\;)(\;4x+240\;)$ 円 ・・・ ①
$1$ 個 $120$ 円で売るときの $1$ 日で売れる金額の合計は,
$120\times 240$(円)… ②
値下げしたときの合計金額 - $1$ 個 $120$ 円で売ったときの合計金額 = $3600$
となればよいので,①,②から,
$(\;120-x\;)(\;4x+240\;)-120\times 240=3600$
$x^{2}-60x+900=0$
$(\;x-30\;)^{2}=0$
$x=30$
よって,$30$ 円値下げすればよいことが分かります。
したがって,$120-30=90$(円)で売るとよい。
《 方程式の計算例 》
$(120-x)(4x+240)-120\times 240=3600$
$-(x-120)\times 4(x+60)-120\times 240=3600$
$\color{red}{\cancelto{1}{\color{black}{-4}}}\color{black}{(x-120)(x+60)}\color{red}{\cancelto{+30}{\color{black}{-120}}}\color{black}{\times 240=}\color{red}{\cancelto{-900}{\color{black}{3600}}}\quad$両辺を $-4$ で割る
$(x-120)(x+60)+7200=-900$
$x^{2}-60x-7200+7200+900=0$
$x^{2}-60x+900=0$
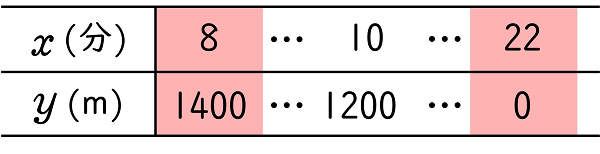
4学校から公園までの $1400$ m の真っ直ぐな道を通り,学校と公園を走って往復する時間を計ることにした。A さんは学校を出発してから $8$ 分後に公園に到着し,公園に到着後は速さを変えて走って戻ったところ,学校を出発してから $22$ 分後に学校に到着した。ただし,A さんの走る速さは,公園に到着する前と後でそれぞれ一定であった。
次の (1),(2) の問いに答えなさい。
(1)A さんが学校を出発してから $x$ 分後の,学校から A さんまでの距離を $y$ m とすると,$x$ と $y$ との関係は下の表のようになった。

(ア)表中の ア,イ に当てはまる数を求めなさい。
解答・解説
解答ア $350$,イ $1200$
問題文より,A さんの走る速さは,公園に到着する前と後でそれぞれ一定です。
〔1〕学校を出発してから公園に到着するまで $(\;0≦x≦8\;)$
公園に到着するまでの $8$ 分間で $1400$ m 走ったので,
その時 $(\;0≦x≦8\;)$ の速さは,
$1400\div 8=175$ (m/分)$1$ 分ごとに $175$ m ずつ学校から離れる
よって,$x=2$(出発して $2$ 分後)のとき
$y=175\times 2=350$ (m)ア$350$
〔2〕公園を出発してから学校に到着するまで $(\;8≦x≦22\;)$
公園から学校に戻るまでの $14$ 分間に $1400$ m 走ったので,
そのとき $(\;8≦x≦22\;)$ の速さは,
$1400\div 14=100$ (m/分)$1$ 分ごとに $100$ m ずつ学校に近づく
$x=10$ である時は,公園を出発して $2$ 分後のことなので,
その $2$ 分間に走った距離は $100\times 2=200$ (m)
よって,
イ $=1400-200=1200$ (m)イ$1200$
(イ)$x$ と $y$ との関係を表すグラフを書きなさい。$(\;0≦x≦22\;)$
解答・解説
解答
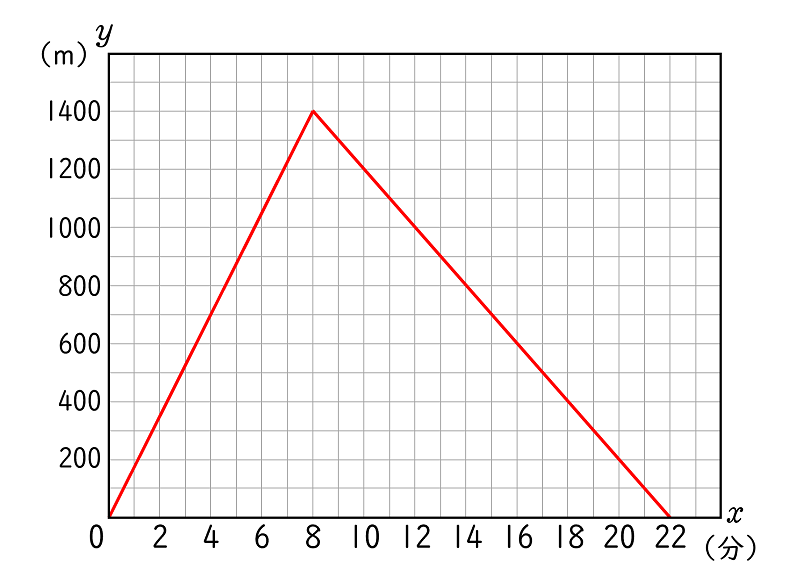
問題文より,A さんの走る速さは,公園に到着する前と後でそれぞれ一定なので,
$0≦x≦8$ の範囲も,$8≦x≦22$ の範囲もグラフは直線( 1 次関数のグラフ)です。
表から,
$0≦x≦8$ の範囲では,座標 $(\;0,0\;)$ と $(\;8,1400\;)$ を結んだ線分
$8≦x≦22$ の範囲では,座標 $(\;8,1400\;)$ と $(\;22,0\;)$ を結んだ線分
になります。
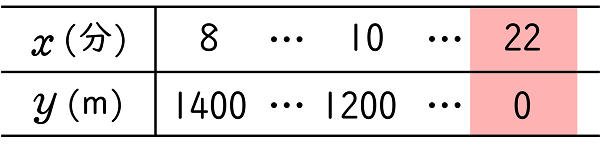
(ウ)$x$ の変域を $8≦x≦22$ とするとき,$x$ と $y$ との関係を式で表しなさい。。
解答・解説
解答$y=-100x+2200$
問題文より,A さんの走る速さは,公園に到着する前と後でそれぞれ一定なので,
$0≦x≦8$ の範囲も,$8≦x≦22$ の範囲も,$y$ は $x$ の 1 次関数です。
求める式を $\;y=ax+b$( $a$ と $b$ は定数 )とおくと,
上の表の $8≦x≦22$ の範囲について,
$a=\dfrac{\;0-1400\;}{22-8}=-100$
よって,求める式は $\;y=-100x+b$ となり,
さらに,$y=-100x+b$ に $x=22$,$y=0$ を代入して,
$0=-100\times 22+b$
$0=-2200+b$
$b=2200$
したがって,$8≦x≦22$ の範囲では,
$y=-100x+2200$
(2)B さんは A さんが学校を出発してから $2$ 分後に学校を出発し,A さんと同じ道を通って公園まで行き,学校に戻った。このとき,B さんは学校を出発してから $8$ 分後に,公園から戻ってきた A さんとすれ違った。B さんは A さんとすれ違った後,すれ違う前より $1$ 分あたり $10$ m 速く走り,A さんに追いついた。ただし,B さんの走る速さは,A さんとすれ違う前と後でそれぞれ一定であった。
(ア)A さんとすれ違った後の B さんの走る速さは,分速何 m であるかを求めなさい。
解答・解説
解答分速 160 m
まず,A さんとすれ違うまでの B さんの速さを求めます。
B さんは A さんが学校を出発した $2$ 分後に学校を出発し,
その $8$ 分後に A さんとすれ違ったので,
B さんとすれ違うまでに A さんが走った時間は,
$2+8=10$(分間)
A さんが学校を出発してから $10$ 分後の場所を求めます。
(1) の (ウ) から,
$y=-100\times 10+2200$
$=1200$ (m)
よって,B さんが A さんとすれ違った場所は,学校から $1200$ m 離れたところです。
つまり,B さんは A さんとすれ違うまでの $8$ 分間で $1200$ m 走ったことになります。
その速さは,
$1200\div 8=150$ (m/分)
B さんは A さんとすれ違った後,それまでより毎分 $10$ m 速く走ったので,
A さんとすれ違った後の B さんの速さは,
$150+10=160$ (m/分)
(イ)B さんが A さんに追いついたのは,A さんが学校を出発してから何分何秒後であるかを求めなさい。
解答・解説
解答$16$ 分 $40$ 秒後
※ A さん → A,B さん → B と表します。
(2)の(ア)から,
B が A とすれ違ったのは 学校から $1200$ m 離れた場所です。
学校から公園までの距離は $1400$ m なので,
$2$ 人がすれ違った場所から公園までの距離は,
$1400-1200=200$ (m) です。
B はその $200$ m を分速 $160$ m で走ったので,
B が A とすれ違ってから公園に着くまでの時間は,
$200\div 160=\small\dfrac{5}{\;4\;}$(分間)
よって,B が公園に着いたのは,
B が学校を出発してから $8+\small \dfrac{5}{\;4\;}=\small \dfrac{\;37\;}{4}$(分後)で,
A が学校を出発してから $\small \dfrac{\;37\;}{4}$$\;+\;2=\small \dfrac{\;45\;}{4}$(分後)です。
さらに,B は公園から学校までの $1400$ m を分速 $160$ m で走ったので,
その時の時間は,
$1400\div 160=\small \dfrac{\;35\;}{4}$(分間)
つまり B が学校に戻ったのは,A が学校を出発してから
$\small \dfrac{\;45\;}{4}+\small \dfrac{\;35\;}{4}=$$\;20$(分後)
このことから, A が学校を出発してから $x$ 分後の,学校から B までの距離を $y$ m とし,
$x$ と $y$ との関係を表とグラフ(青線)に表すと下のようになります。
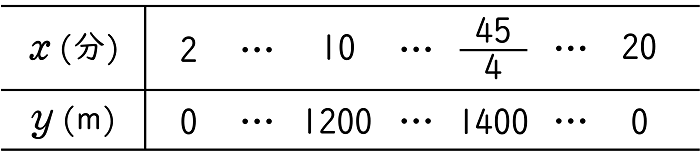
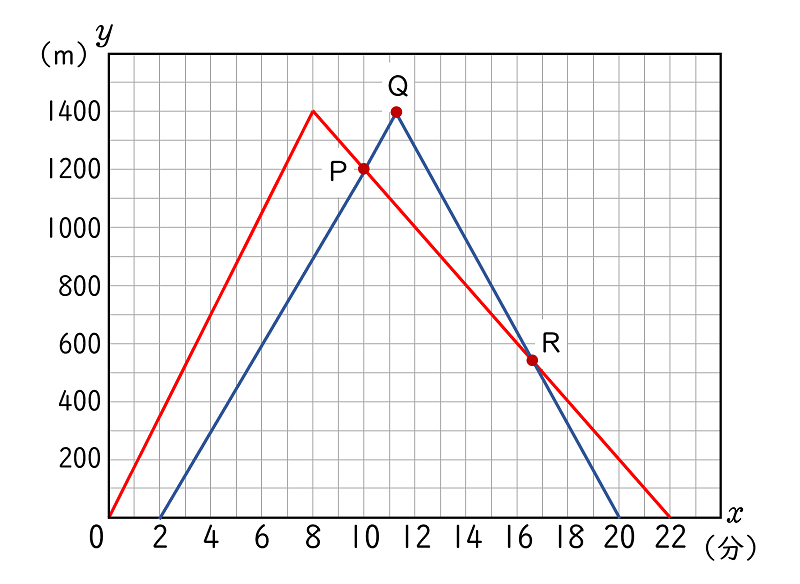
グラフの点 P の座標が $(\;10,1200\;)$,点 Q の座標が $\left(\;\small \dfrac{\;45\;}{4}\normalsize,1400\;\right)$,で,
B が A に追いつく時間と場所は 点 R の座標から求めることができます。
$\small\dfrac{\;45\;}{4}$$≦x≦20$ の範囲の B のグラフの式を求めます。
求める式を $\;y=ax+b$( $a$ と $b$ は定数 )とおくと,
上の表の $\small \dfrac{\;45\;}{4}$$≦x≦20$ の範囲について,
$a= \small\dfrac{\;0-1400\;}{20- \frac{\;45\;}{4}}\normalsize=-1400\div \dfrac{\;35\;}{4}\normalsize=-160$
よって,求める式は $\;y=-160x+b$ となり,
さらに,この式に $x=20$,$y=0$ を代入して,
$0=-160\times 20+b$
$0=-3200+b$
$b=3200$
したがって,$ \small \dfrac{\;45\;}{4}$$≦x≦20$ の範囲では,
$y=-160x+3200$
また (1) の (ウ) から,$ \small\dfrac{\;45\;}{4}$$≦x≦20$ の範囲の A のグラフの式は,
$y=-100x+2200$
グラフの点 R の座標は,下の連立方程式を解くことで求められます。
$\;\left\{\begin{array}{l}y=-160x+3200\\y=-100x+2200\end{array}\right.\;$
$-160x+3200=-100x+2200$
$x=\dfrac{\;50\;}{3}$
$\dfrac{\;50\;}{3}\;$ 分 $=16\dfrac{\;2\;}{3}\;$ 分$=16$ 分 $40$ 秒$\dfrac{\;2\;}{3}$ 分 $=60\times\dfrac{\;2\;}{3}$(秒)$=40$ 秒
B が A に追いついたのは,A が学校を出発してから $16$ 分 $40$ 秒後です。
方程式による解
$2$ 人がすれ違ってから,B が A に追いつくまでの間を考えます。
(2) の (ア) から,$2$ 人がすれ違ったとき,
A は公園から学校に向かって走り,公園から $200$ m の場所を通過し,
B は学校から公園に向かって走り,公園まで $200$ m の場所を通過しています。
よって,その時の $2$ 人の間の距離は $200\times 2=400$ (m) です。
$2$ 人がすれ違ってから,B が A に追いつくまでに $t$ 分かかったとすると,
その $t$ 分間に B は A より $400$ m 長い距離を走り,A に追いついたことになります。
$t$ 分間に B が走った距離 = $t$ 分間に A が走った距離 + $400$ m
(1) の (ア) および (2) の (ア) から,
そのときの A の速さは毎分 $100$ m,B の速さは 毎分 $160$ m です。
$160t=100t+400$
$t=\small{\dfrac{\;20\;}{3}}$(分)
$2$ 人がすれ違ったのは,A が学校を出発して $10$ 分後だから,
B が A に追いついたのは,A が学校を出発してから
$10+\dfrac{\;20\;}{3}=16\dfrac{\;2\;}{3}$ (分) = $16$ 分 $40$ 秒
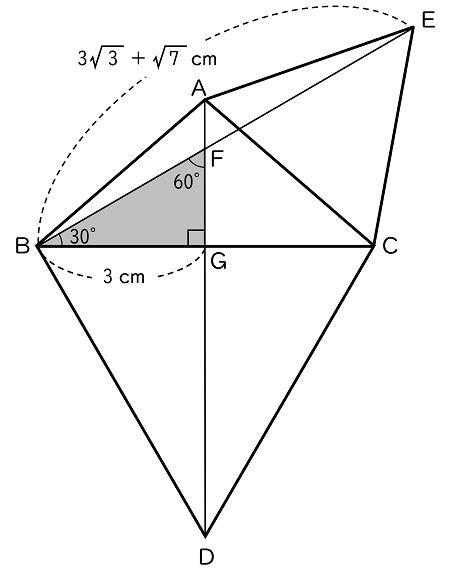
5下の図で,△BDC と △ACE はともに正三角形である。また,線分 AD と BE との交点を F,AD と BC との交点を G とする。
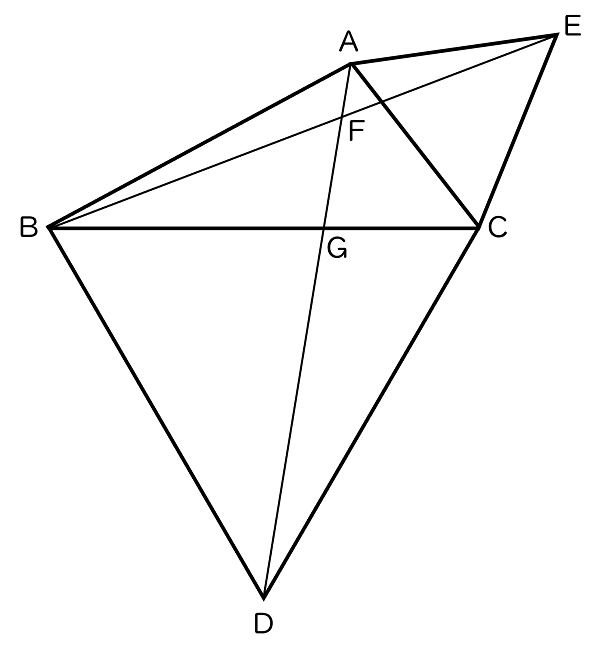
次の (1),(2) の問いに答えなさい。
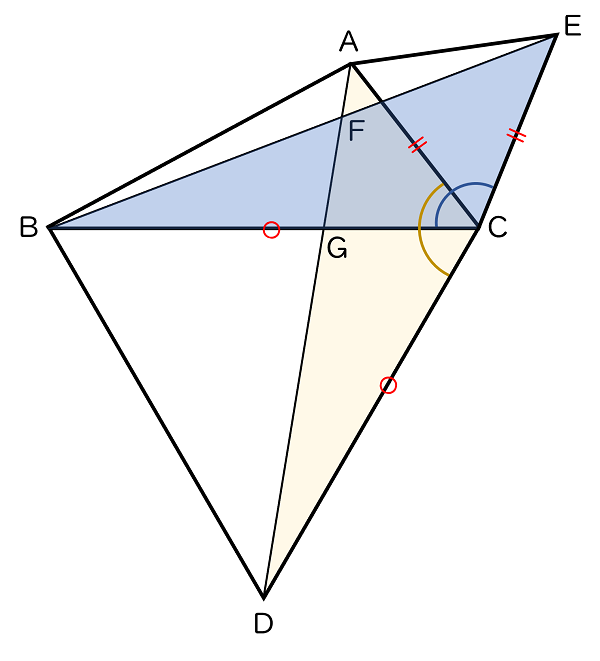
(1)△ADC ≡ △EBC であることを証明しなさい。
解答
〈仮定〉△BDC と △ACE はともに正三角形
〈結論〉△ADC ≡ △EBC
〈証明〉
△ADC と △EBC で,
仮定から,DC = BC・・・・・・①
仮定から,CA = CE・・・・・・②
仮定から,∠BCD = ∠ECA = 60°・・・・・・③
また,∠ACD = ∠ACB + ∠BCD・・・・・・④
∠ECB = ∠ACB + ∠ECA・・・・・・⑤
③,④,⑤から,∠ACD = ∠ECB・・・・・・⑥
①,②,⑥から,2 組の辺とその間の角がそれぞれ等しいので,
△ADC ≡ △EBC
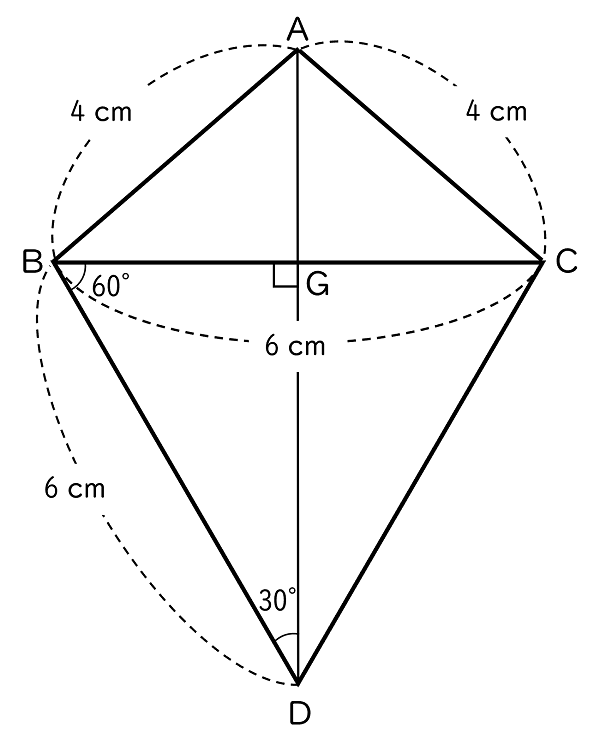
(2)AB $=4$ cm,AC $=4$ cm,BC $=6$ cm のとき,
(ア)DG の長さを求めなさい。
解答・解説
解答$3\sqrt{\,3\,}$ cm
仮定から,△BDG は $1$ 辺が $6$ cm の正三角形であり,
△ABD ≡ △ACD(証明は下)だから,
∠BDG $=$ ∠CDG $=60° \times \dfrac{1}{\;2\;}=30°$
二等辺三角形の頂角(∠BDC)の二等分線(DG)は底辺(BC)を垂直に二等分するから,
∠DGB $=90°$
よって,△BDG は
BD:DG $=2$:$\sqrt{\,3\,}$
となる直角三角形である。
BD$=6$ cm だから,
$6$:DG $=2$:$\sqrt{\,3\,}$
DG $=3\sqrt{\,3\,}$
〔 次の(イ)で使う AD の長さを求めておきます 〕
さらに,
BG $=6 \times \dfrac{1}{\;2\;}=3$ (cm),∠AGB $=90°$
であり,△ABG について三平方の定理から,
AG $=\sqrt{\sf\small AB^{2}-BG^{2}}=\sqrt{\,4^{2}-3^{2}\,}=\sqrt{\,7\,}$ (cm)
よって,AD $=$ DG $+$ AG $=3\sqrt{\,3\,}+\sqrt{\,7\,}$ (cm)
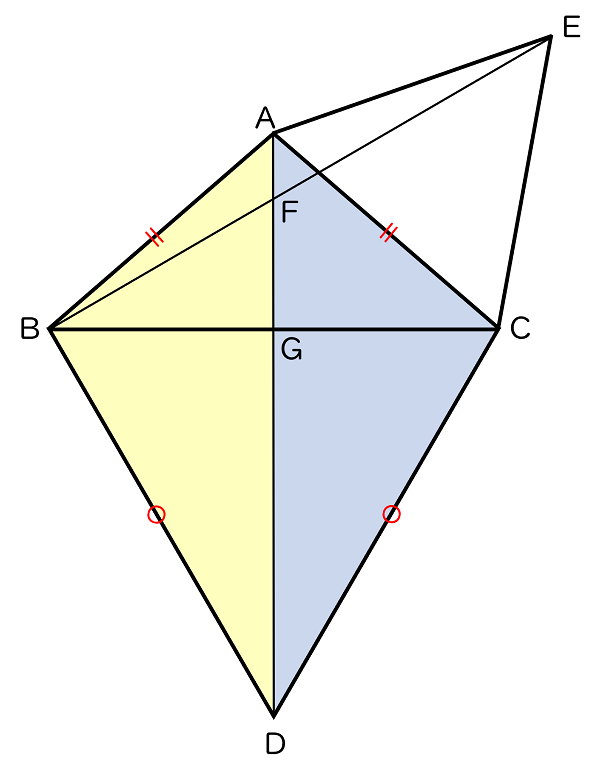
△ABD ≡ △ACD の証明
〈仮定〉△BDCは正三角形,AB = AC
〈結論〉△ABD ≡ △ACD
〈証明〉
△ABD と △ACD で,
仮定から,AB = AC・・・・・・①
仮定から,AB = AC・・・・・・②
共通な辺だから,AD = AD・・・・・・③
①,②,③から,3 組の辺がそれぞれ等しいので,
△ABD ≡ △ACD
(イ)EF の長さを求めなさい。
解答・解説
解答$\sqrt{\,3\,}+\sqrt{\,7\,}$ cm
(1) から,△ADC ≡ △EBC だから,
∠ADC $=$ ∠EBC
(2) の (ア) から,
∠ADC $=30°$
よって,
∠EBC $=$ ∠FBG $=30°$
さらに,BG $=3$ cm,∠AGB $=90°$ だから,
△FBG は右図のような直角三角形になります。
BF:BG $=2$:$\sqrt{\,3\,}$
BF:$3=2$:$\sqrt{\,3\,}$
BF $=2\sqrt{\,3\,}$ ……①
(1) から,△ADC ≡ △EBC だから,
AD $=$ EB
(2) の (ア) から,
AD $=3\sqrt{\,3\,}+\sqrt{\,7\,}$ (cm)
よって,
EB $= 3\sqrt{\,3\,}+\sqrt{\,7\,}$ (cm) ・・・・・・②
①,②から,
EF $=$ EB $-$ BF
$=( 3\sqrt{\,3\,}+\sqrt{\,7\,})-2\sqrt{\,3\,}$
$=\sqrt{\,3\,}+\sqrt{\,7\,}$ (cm)
6右の表 1 は,かけ算の九九を表にしたものである。太郎さんは,表 1 の太枠の中に書かれた $81$ 個の数字の合計を工夫して求めようとした。
次の (1),(2) の問いに答えなさい。
(1)太郎さんは,表 1 の太枠の中から一部を取り出し,$4$ 段 $4$ 列の表 2 を作った。さらに,表 2 をもとに次のように表 3,表 4,表 5 をそれぞれ作り,表 2 に書かれた $16$ 個の数字の合計を考えた。
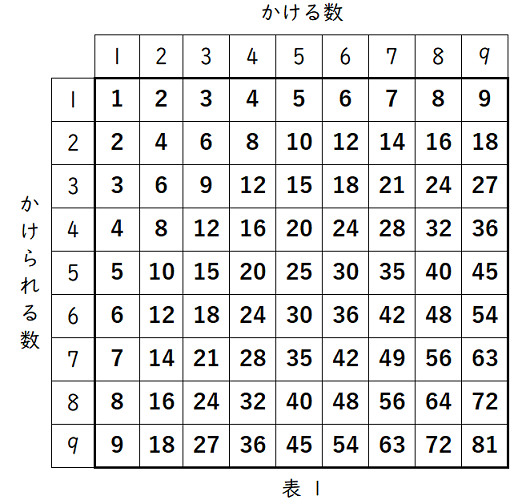
表 3 は,表 2 の数字を左右対称に並べ替えたもの。
表 4 は,表 2 の数字を上下対称に並べ替えたもの。
表 5 は,表 2 の数字を左右対称に並べ替え,さらに上下対称に並べ替えたもの。

次の文章は,太郎さんの考えをまとめたものである。ア,イ,オ,カ には数を,ウ には $b$ を使った式を,エ には $a$ を使った式を,それぞれあてはまるように書きなさい。
表 2,表 3,表 4,表 5 について,各表の上から $3$ 段目,左から $2$ 列目に書かれた数字は,順に,$6$,ア ,$4$,$6$ であり,合計は イ となる。同様に,他の位置に書かれた数字について,各表の上から $a$ 段目,左から $b$ 段目に書かれた数字を $a$,$b$ を使って表すと,順に,$ab$,$a$( ウ ),( エ )$b$,( エ )( ウ ) であり,合計すると オ となる。
したがって,表 2 に書かれた $16$ 個の数字の合計は $\;\sf\dfrac{\,\framebox[1.5cm][c]{オ}\times 16\,}{\framebox[1.5cm][c]{カ}}\;$で計算できる。
解答・解説
解答ア $9$ イ $25$ ウ $5-b$ エ $5-a$ オ $25$ カ $4$
表 3 は,表 2 の数字を左右対称に並び替えたものだから,
表 3 の $3$ 段目は,表 2 の $3$ 段目を左右対称に並び替えして,
$12$$9$$6$$3$
となります。ア$9$
各表の上から $3$ 段目,左から $2$ 列目に書かれた数字の和は,
$6+9+4+6=25$イ$25$
他の位置に書かれた数字について,
各表の上から $a$ 段目,左から $b$ 列目に書かれた数字を考えます。
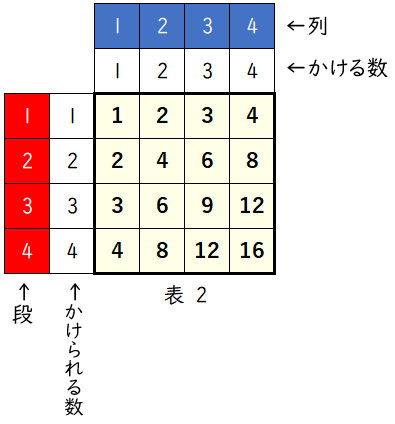
表 2 では,
段数とかけられる数,列数とかける数がそれぞれ同じです。
よって,上から $a$ 段目,左から $b$ 列目に書かれた数字は
$a$ × $b$ = $ab$
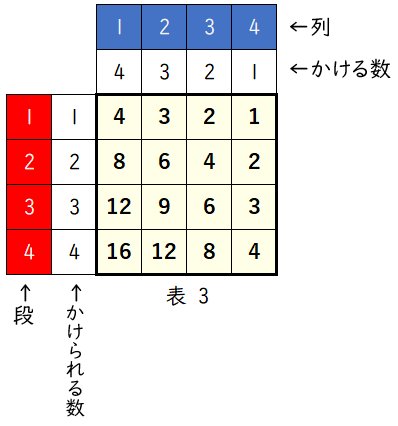
表 3 では,
段数とかけられる数は同じだから,$a$ 段のかけられる数は $a$ です。
列数とかける数は左右対称になっており,
列数 + かける数 $=5$
かける数 $=5-$ 列数
になっています。
よって,$b$ 列のかける数は $5-b$ です。
したがって,上から $a$ 段目,左から $b$ 列目に書かれた数字は
$a\times(\,5-b\,)=a(\,5-b\,)$ウ$5-b$
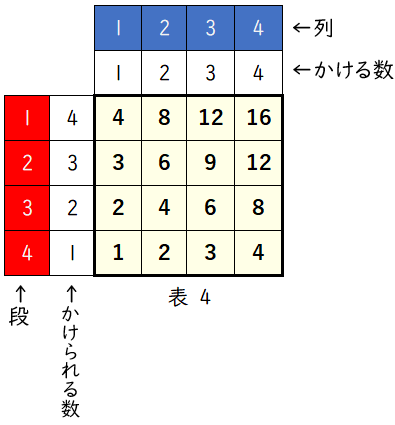
表 4 では,
段数とかけられる数が上下対称となっており,
段数 + かけられる数 $=5$
かけられる数 $=5-$ 段数
になっています。
よって,$a$ 段のかけられる数は $5-a$ です。
列数とかける数は同じだから,$b$ 列のかける数は $b$ です。
したがって,上から $a$ 段目,左から $b$ 列目に書かれた数字は
$(\,5-a\,)\times b=(\,5-a\,)b$エ$5-a$
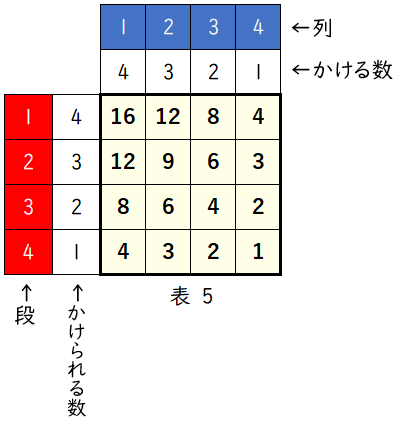
表 5 では,
段数とかけられる数が上下対称となっており,
列数とかける数は左右対称になっています。
よって,
$a$ 段のかけられる数は $5-a$
$b$ 列のかける数は $5-b$
です。
したがって,上から $a$ 段目,左から $b$ 列目に書かれた数字は
$(\,5-a\,)\times (\,5-b\,)=(\,5-a\,)(\,5-b\,)$
以上から,各表の上から $a$ 段目,左から $b$ 段目に書かれた数字の合計は,
$ab+a(\,5-b\,)+(\,5-a\,)b+(\,5-a\,)(\,5-b\,)$
$=ab+(\,5a-ab\,)+(\,5b-ab\,)+(\,25-5b-5a+ab\,)$
$=25$オ$25$
$4$ つの表のすべての場所の数字についても,その合計は $25$ になります。
よって,$4$ つの表すべての数の合計は,$25\times 16$ になり,
表 2 だけの数字の合計は,その $ \small \dfrac{1}{\;4\;}$です。
表 2 に書かれた $16$ 個の数字の合計は,$\dfrac{\;25\;\times\;16\;}{\color{red}4}=100$カ$4$
(2)表 1 の太枠の中に書かれた $81$ 個の数字の合計を求めなさい。
解答・解説
解答$2025$
表 1 についても (1) と同じように表をあと $3$ つ作ったとします。
(1) と同様に考えると,$4$ つの表の上から $a$ 段目,左から $b$ 列目の数字はそれぞれ,
$ab$, $a(\,10-b\,)$, $(\,10-a\,)b$, $(\,10-a\,)(\,10-b\,)$
になります。
よって,それらの合計は,
$ab+a(\,10-b\,)+(\,10-a\,)b+(\,10-a\,)(\,10-b\,)$
$=ab+(\,10a-ab\,)+(\,10b-ab\,)+(\,100-10b-10a+ab\,)$
$=100$
$4$ つの表のすべての場所の数字についても,その合計は $100$ になります。
よって,$4$ つの表すべての数の合計は,$100\times 81$ になり,
表 1 に書かれた $81$ 個の数字の合計は,$ \small \dfrac{\;100\;\times\;81\;}{4}$ $=2025$

