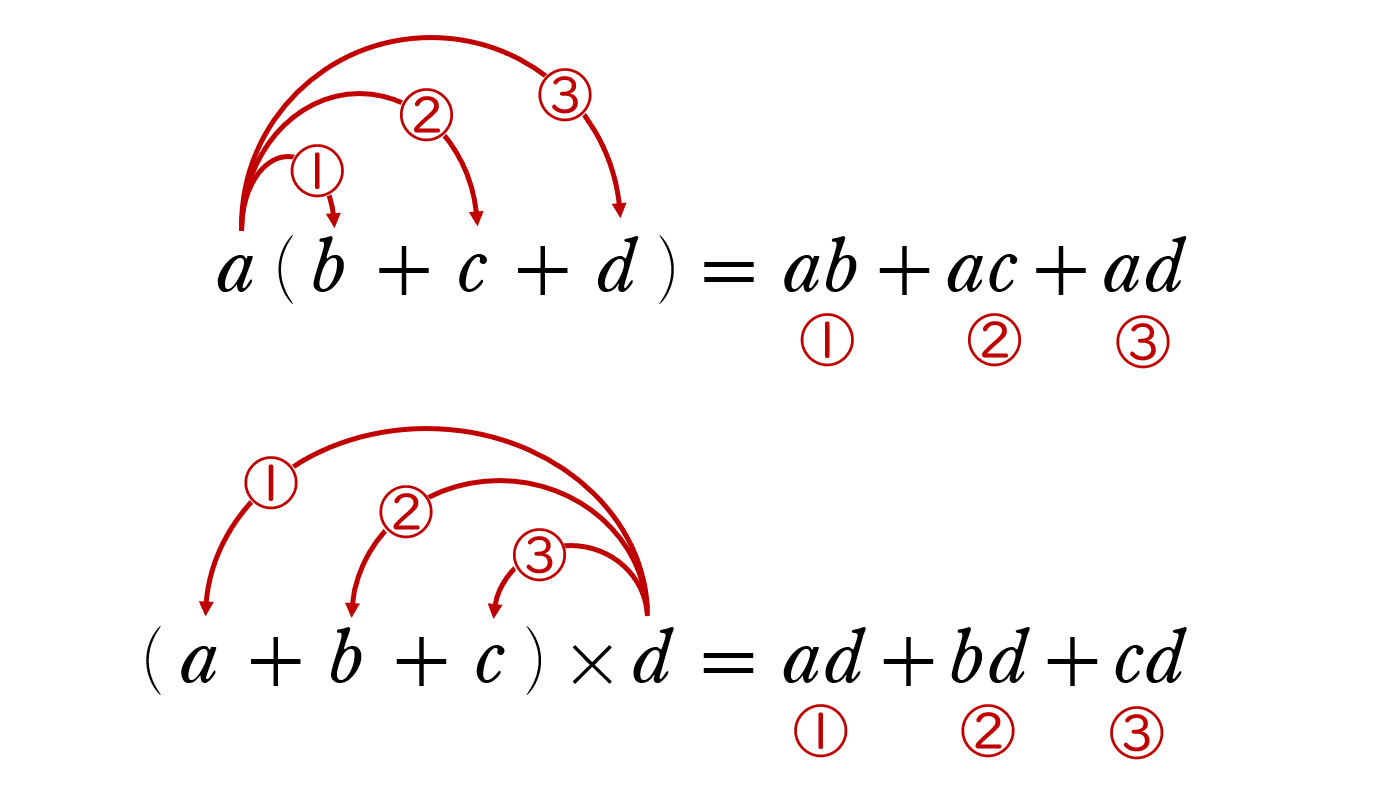31012中３・多項式の展開・計算問題・分配法則2

(1) $\;\;\;\begin{eqnarray}3a(2a-4b+5c)\end{eqnarray}\;\;$

$\;\;\begin{eqnarray}&=&3a \times 2a+3a \times (-4b)+3a \times 5c\\[5pt]&=&6a^{2}-12ab+15ac\end{eqnarray}\;\;$

答$6a^{2}-12ab+15ac$

(2) $\;\;\;\begin{eqnarray} -7x(-x+2y-1) \end{eqnarray}\;\;$

$\;\;\begin{eqnarray}&=&-7x \times (-x)-7x\times 2y -7x\times (-1)\\[5pt]&=&7x^{2}-14xy+7x\end{eqnarray}\;\;$

答$7x^{2}-14xy+7x$

(3) $\,\;\;\;\begin{eqnarray}-\frac{2}{\;3\;}a(6a-12b-21c)\end{eqnarray}\;\;$

$\;\;\begin{eqnarray} &=& -\frac{2}{\;3\;}a \times 6a -\frac{2}{\;3\;}a \times (-12b) -\frac{2}{\;3\;}a \times (-21c) \\[5pt]&=&-4a^{2}+8ab+14ac\end{eqnarray}\;\;$

答$-4a^{2}+8ab+14ac$

(4) $\;\;\begin{eqnarray}(9x-4xy+3y)\times (-5x)\end{eqnarray}\;\;$

$\;\;\begin{eqnarray} &=& 9x\times (-5x)-4xy\times (-5x)+3y\times (-5x)\\[5pt]&=&-45x^{2}+20x^{2}y-15xy\end{eqnarray}\;\;$

答$-45x^{2}+20x^{2}y-15xy$

(5) $\;\;\;\begin{eqnarray} (-8a-20ab+16b)\times \Bigl(-\frac{b}{\;4\;}\Bigr)\end{eqnarray}\;\;$

$\;\;\begin{eqnarray} &=& -8a\times \Bigl(-\frac{b}{\;4\;}\Bigr) -20ab\times \Bigl(-\frac{b}{\;4\;}\Bigr) +16b\times \Bigl(-\frac{b}{\;4\;}\Bigr) \\[5pt]&=& 2ab+5ab^{2}-4b^{2}\end{eqnarray}\;\;$

答$2ab+5ab^{2}-4b^{2}$