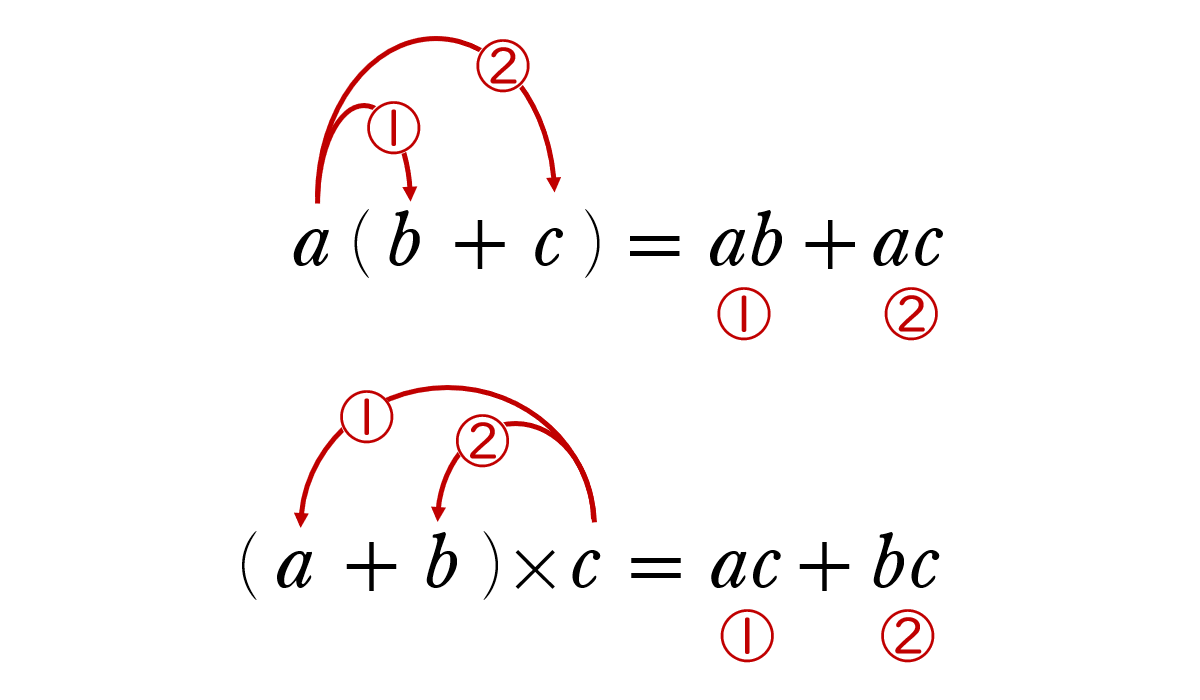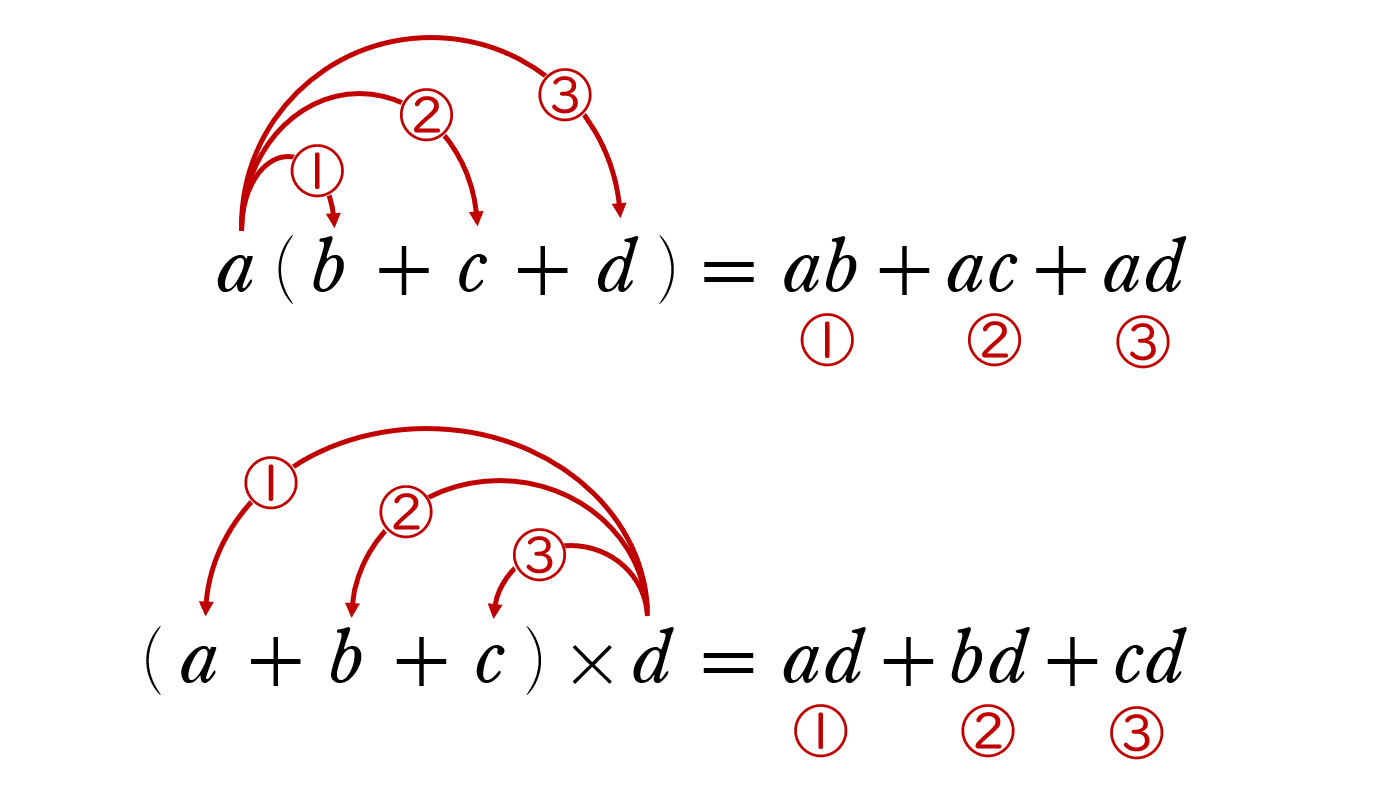21071中２・式の計算・計算問題・多項式と数の乗法1

分 配 法 則

１．①，②の順にかけ合わせます

２．①，②，③の順にかけ合わせます

$\begin{eqnarray}(1)\quad\;\;3(\,x+5y\,)\end{eqnarray}\;\;$

$\begin{eqnarray}\quad\;\;&=&\color{red}3\times\color{black}x\color{red}+3 \times \color{black}5y\\[5pt]&=&3x+15y\end{eqnarray}\;\;$

答$3x+15y$

$\begin{eqnarray}(2)\quad\;\;-5(\,2a-6b\,)\end{eqnarray}\;\;$

$\begin{eqnarray}\quad\;\;&=&\color{red}-5 \times\color{black}2a\color{red}-5 \times\color{black}(\,-6b\,)\\[5pt]&=&-10a+30b\end{eqnarray}\;\;$

答$-10a+30b$

$\begin{eqnarray}(3)\quad\;\;8(\,-3x+5y-4\,)\end{eqnarray}\;\;$

$\begin{eqnarray}\quad\;\;&=&\color{red}8 \times\color{black}(\,-3x\,)\color{red}+8 \times\color{black}5y\color{red}+8 \times\color{black} (\,-4\,)\\[5pt]&=&-24x+40y-32\end{eqnarray}\;\;$

答$-24x+40y-32$

$\begin{eqnarray}(4)\quad\;\;(\,-6a-9b\,)\times 2\end{eqnarray}\;\;$

$\begin{eqnarray}\quad\;\;&=&-6a\color{red}\times 2\color{black}-9b\color{red}\times 2\color{black}\\[5pt]&=&-12a-18b\end{eqnarray}\;\;$

答$-12a-18b$

$\begin{eqnarray}(5)\quad\;\;(\,4x^{2}-3x+5\,)\times (\,-7\,)\end{eqnarray}\;\;$

$\begin{eqnarray}\quad\;\;&=&4x^{2}\color{red}\times (\,-7\,)\color{black}-3x\color{red}\times (\,-7\,)\color{black}+5\color{red}\times (\,-7\,)\color{black}\\[5pt]&=&-28x^{2}+21x-35\end{eqnarray}\;\;$

答$-28x^{2}+21x-35$

$\begin{eqnarray}(6)\quad\;\;(\,-2a^{2}+7ab-b^{2}\,)\times (\,-4\,)\end{eqnarray}\;\;$

$\begin{eqnarray}\quad\;\;&=&-2a^{2}\color{red}\times (\,-4\,)\color{black}+7ab\color{red}\times (\,-4\,)\color{black}-b^{2}\color{red}\times (\,-4\,)\color{black}\\[5pt]&=&8a^{2}-28ab+4b^{2}\end{eqnarray}\;\;$

答$8a^{2}-28ab+4b^{2}$