岐阜県・公立高校入試 2025年度( 令和7年度 )解答・解説編
岐阜県立高校・入学試験学力検査・数学・2025年度
1次の(1)~(6)の問いに答えなさい。
(1)$(\,-3\,) \times 4+5\;\;$を計算しなさい。
解答・解説
解答$-7$
$\color{red}(\,-3\,) \times 4 \color{black}+5$
$=-12+5$
$=-7$
(2)$3x-y=4\;\;$を $y$ について解きなさい。
解答・解説
解答$y=3x-4$
$\begin{eqnarray}
3x-y &=& 4 \\[7pt] -y &=& -3x+4 \\[7pt] y &=& 3x-4 \end{eqnarray}$
(3)$(\,\sqrt{\,6\,}-2\,)(\,\sqrt{\,6\,}+2\,)\;\;$を計算しなさい。
解答・解説
解答$2$
$(\,\sqrt{\,6\,}-2\,)(\,\sqrt{\,6\,}+2\,)$
$=(\,\sqrt{\,6\,}\,)^2-2^2$
$=6-4$
$=2$
(4)$y$ が $x$ に反比例するものを,ア ~ エ から $1$ つ選び,符号で書きなさい。
ア$1$ 辺が $x\;\rm cm$ の正方形の面積が $y\;\rm cm^2$
イ長さが $60\;\rm cm$ のリボンを $x\;\rm cm$ 使ったとき,残りの長さが $y\;\rm cm$
ウ分速 $130\;\rm m$ で $x$ 分間走ったとき,進んだ道のりが $y\;\rm cm$
エ$10\;\rm L$ 入る空の容器に毎分 $x\;\rm L$ ずつ水を入れたとき,満水になるまでにかかる時間は $y$ 分
解答・解説
ー
解答エ
ア$1$ 辺が $x\;\rm cm$ の正方形の面積が $y\;\rm cm^2$
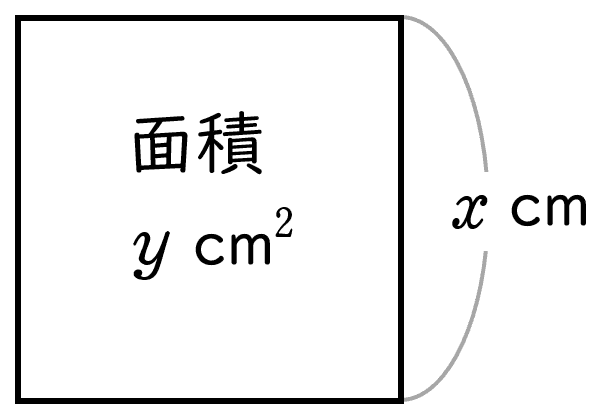
式は $\;\;y=x^2\;\;$ となるので,$y$ は $x$ に反比例しません。
イ長さが $60\;\rm cm$ のリボンを $x\;\rm cm$ 使ったとき,残りの長さが $y\;\rm cm$
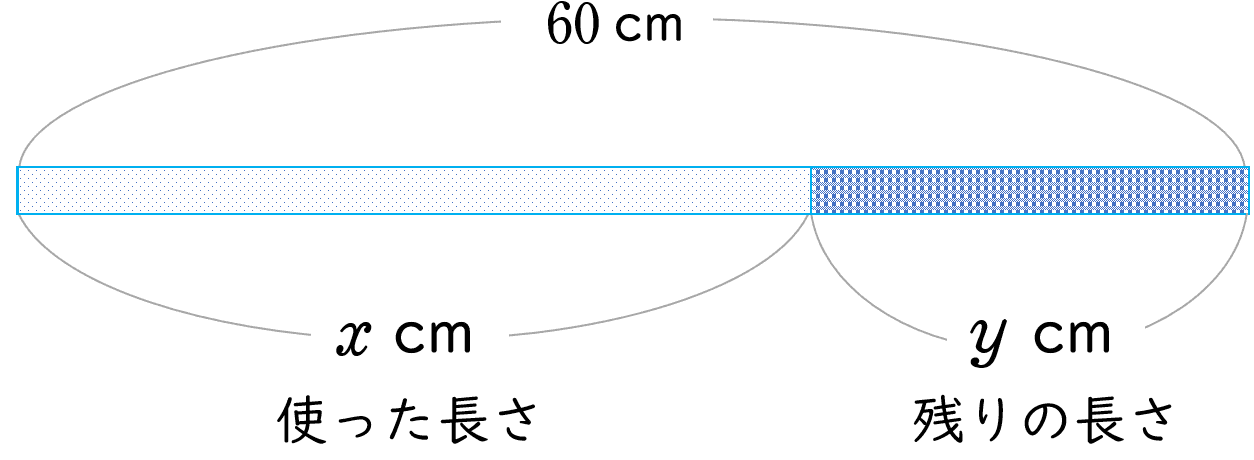
式は $\;\;y=60-x\;\;$ となるので,$y$ は $x$ に反比例しません。
ウ分速 $130\;\rm m$ で $x$ 分間走ったとき,進んだ道のりが $y\;\rm cm$
分速 $130\;\rm m$ で $x$ 分間走ったとき,進んだ道のりは
$130 \times x = 130x$ ($\rm m$)です。
よって式は $\;\;y=130x\;\;$ となるので,$y$ は $x$ に反比例しません。
エ$10\;\rm L$ 入る空の容器に毎分 $x\;\rm L$ ずつ水を入れたとき,満水になるまでにかかる時間は $y$ 分
毎分 $x\;\rm L$ ずつ入れていくと,$10\;\rm L$ 入るまでにかかる時間は
$10 \div x= \dfrac{\;10\;}{x}$ (分) です。
よって式は $\;\;y=\dfrac{\;10\;}{x}\;\;$ となるので,$y$ が $x$ に反比例します。
(5)A 賞,B 賞,C 賞のくじが $1$ 本ずつ合計 $3$ 本のくじが入っている箱がある。この中から $1$ 本引き,それを箱に戻してよくかき混ぜてから,もう $1$ 本引く。このとき,A 賞と B 賞のくじを $1$ 本ずつ引く確率を求めなさい。
解答・解説
解答$\dfrac{2}{\,9\,}$
くじの引き方のすべての場合を樹形図(下の図)に表します。
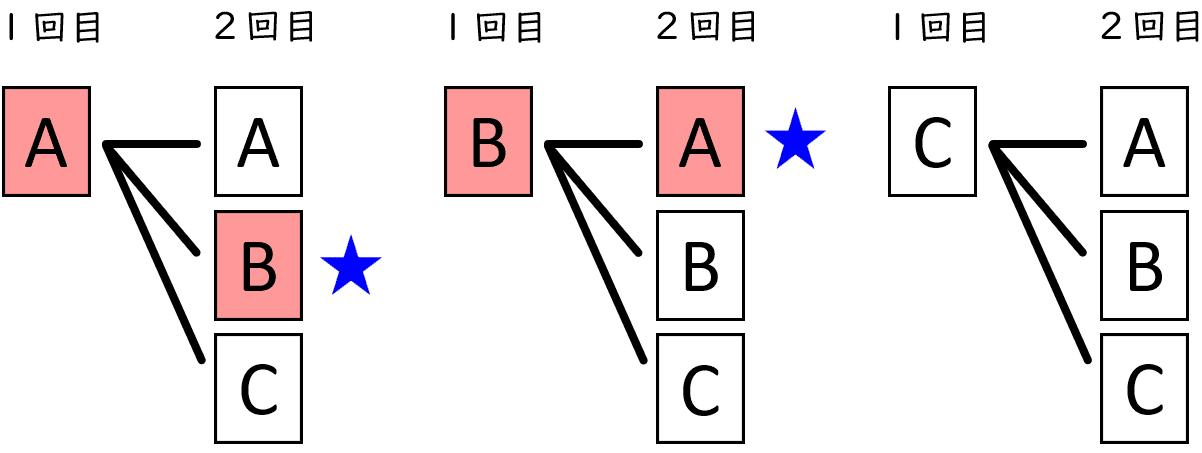
すべての場合の数は,$3 \times 3 = 9$(通り)です。
A 賞と B 賞のくじを $1$ 本ずつ引く場合の数は,上の図の★の $2$ 通りです。
よって,A 賞と B 賞のくじを $1$ 本ずつ引く確率は
$\dfrac{2}{\;9\;}$
この式に $x=-3$ を代入すると,
$\begin{eqnarray}
y &=& \dfrac{a}{\;x\;} \\ xy &=& a \end{eqnarray}$
$\begin{eqnarray}
y &=& -60 \div (\;-3\;)\\
&=& 20
\end{eqnarray}$
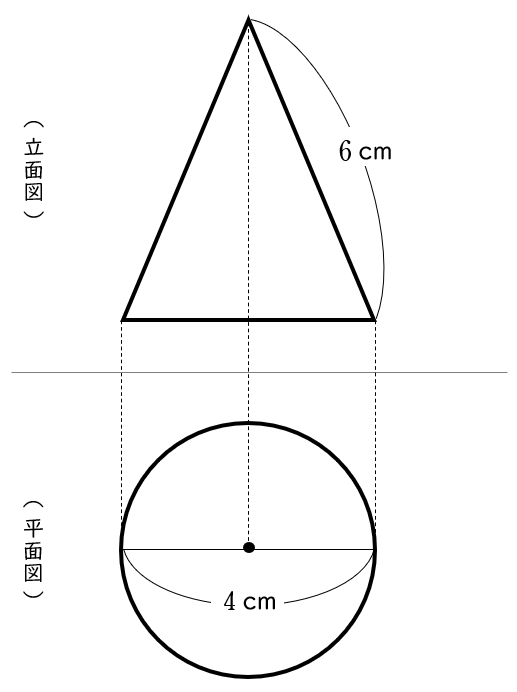
(6)下の図は,円すいの投影図であり,立面図は二等辺三角形,平面図は円である。この円すいの展開図について,側面になるおうぎ形の中心角の大きさを求めなさい。
解答・解説
解答$120°$
【解法1】
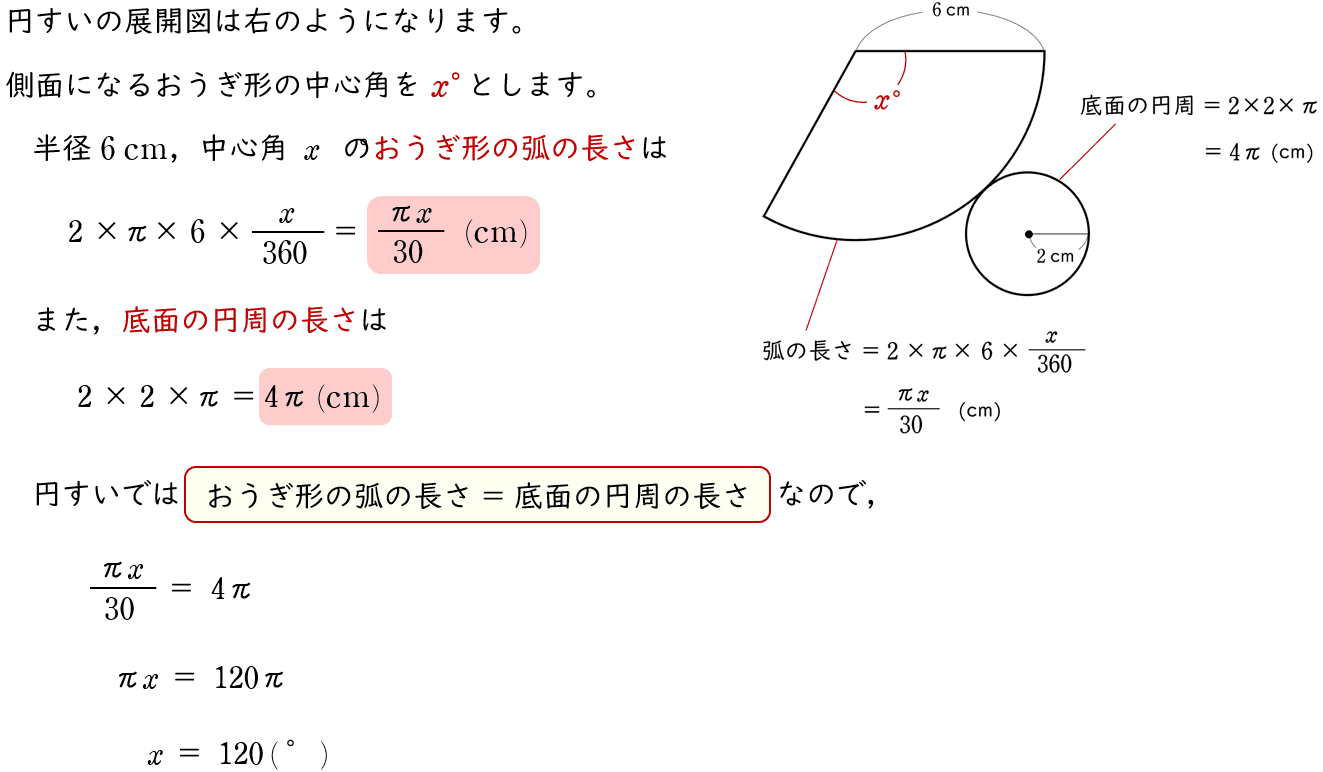
【解法2】
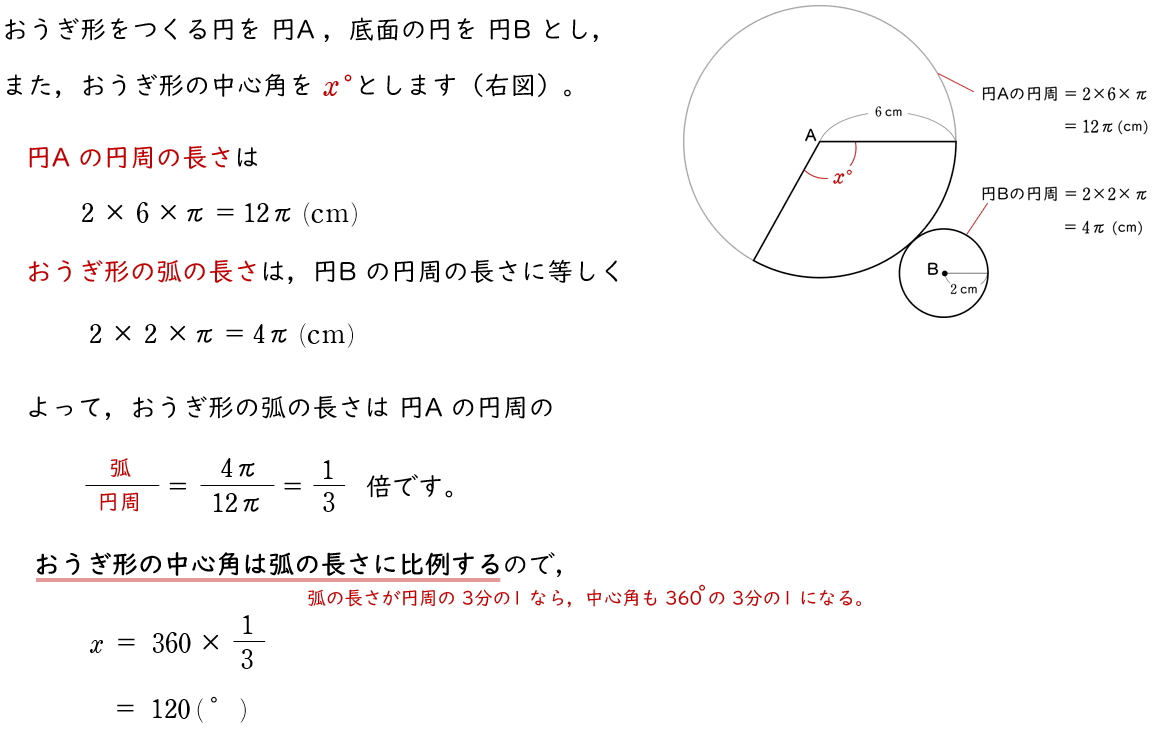
2連続する $3$ つの自然数について,最も小さい自然数を $x$ とする。
次の (1)~(3) の問いに答えなさい。
(1)連続する $3$ つの自然数のうち,最も大きい自然数を $x$ を使った式で表しなさい。
解答・解説
解答$x+2$
連続する $3$ つの自然数は,最も小さい自然数を $x$ とすると,
$x$,$x+1$,$x+2$
と表せます。
よって,最も大きい自然数は $\;\;x+2\;\;$ です。
(2)連続する $3$ つの自然数のそれぞれの $2$ 乗の和を,$ax^2+bx+c\;$ の形で表しなさい。
解答・解説
解答$3x^2+6x+5$
連続する $3$ つの自然数のそれぞれの $2$ 乗の和は
$x^2+(\,x+1\,)^2+(\,x+2\,)^2$
です。式を展開して整理します。
$\begin{eqnarray}
x^2+(\,x+1\,)^2+(\,x+2\,)^2 &=& x^2+(\,x^2+2x+1\,)+(\,x^2+4x+4\,)\\[3pt]
&=& 3x^2+6x+5
\end{eqnarray}$
(3)連続する $3$ つの自然数のそれぞれの $2$ 乗の和が $245$ であるとき,$x$ の値を求めなさい。
解答・解説
解答$8$
(2) から,連続する $3$ つの自然数のそれぞれの $2$ 乗の和は
$3x^2+6x+5$
です。これが $245$ であるとき,次の方程式ができます。
$3x^2+6x+5=245$
方程式を解きます。
$\begin{eqnarray}
3x^2+6x+5 &=& 245\\[3pt]
3x^2+6x-240&=& 0\\[3pt]
x^2+2x-80&=& 0\\[3pt]
\quad(\,x-8\,)(\,x+10\,)&=& 0\\[3pt]
x=8,\;x=-10\end{eqnarray}$
$x$ は自然数だから$\;\; x=8$
3下の表は,A 中学校の生徒 $50$ 人と B 中学校の生徒 $20$ 人について,ある日の家庭学習時間の相対度数を表したものである。
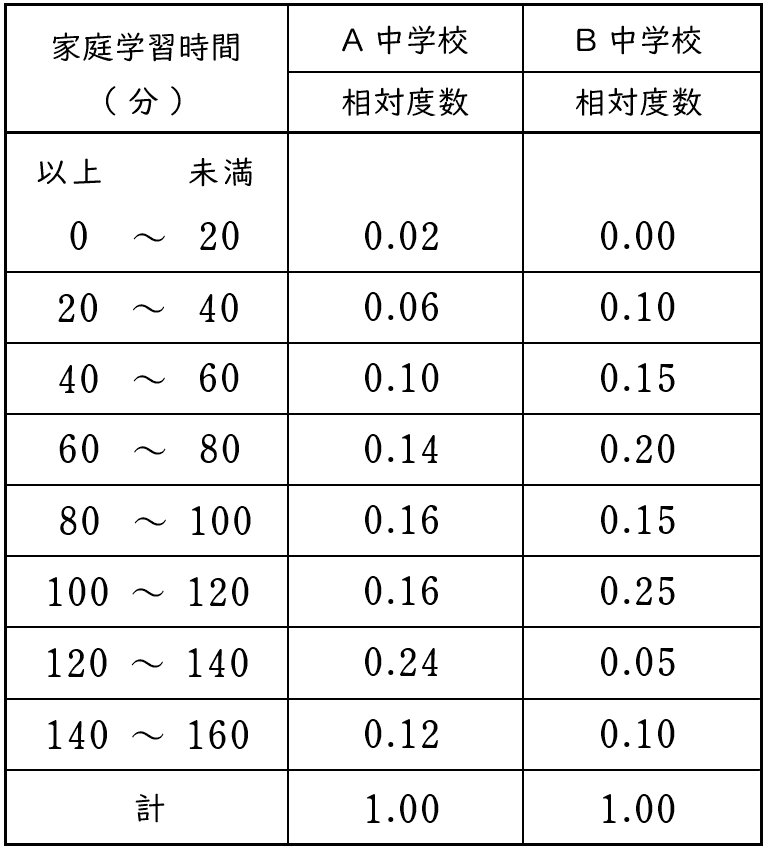
次の (1) ~ (3) の問いに答えなさい。
(1)A 中学校の家庭学習時間の最頻値を求めなさい。
解答・解説
解答$130$
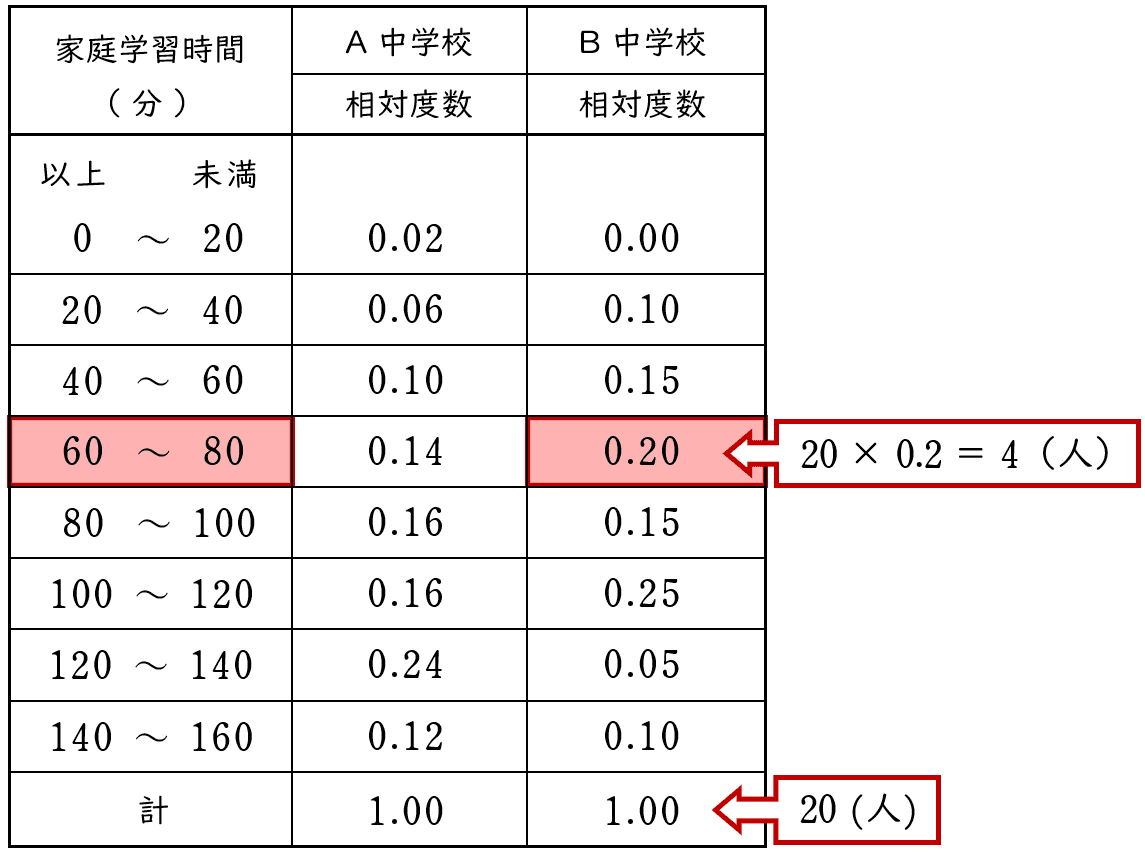
最頻値は度数(または相対度数)が最も大きい階級の階級値です。
表から,A 中学校の相対度数が最も大きい階級は「$120$ 分以上 $140$ 分未満の階級」で,
その階級値は $\;\;\dfrac{\;120+140\;}{2}=130\;\;$ です。
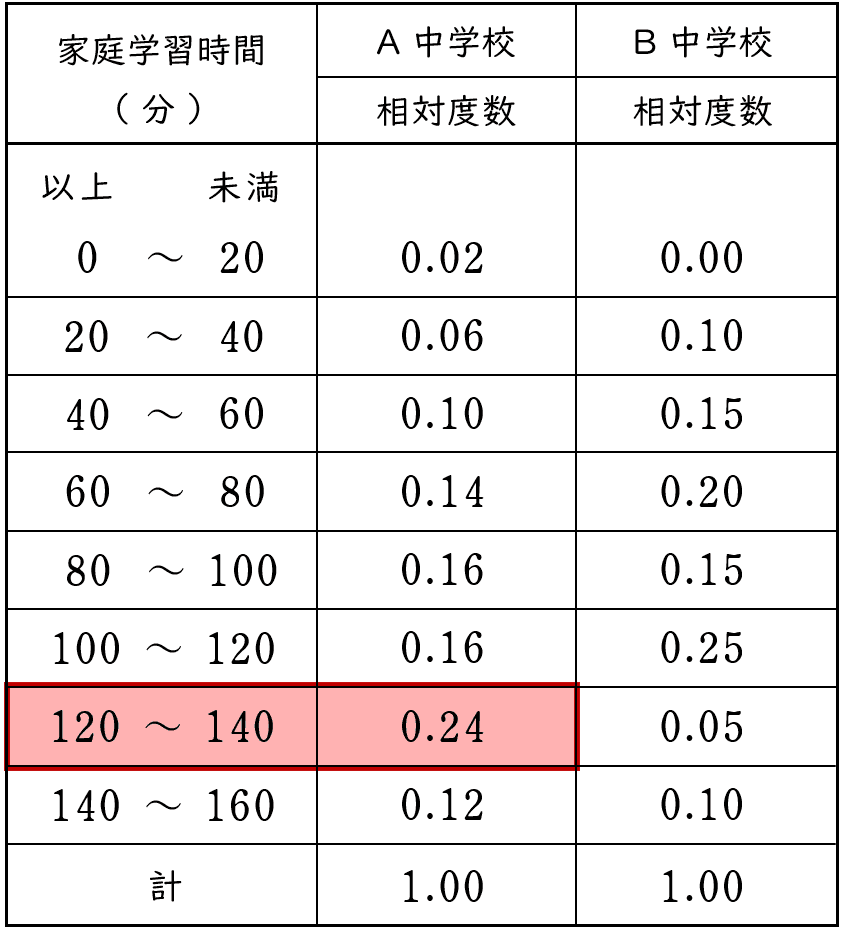
(2)B 中学校で,家庭学習時間が $60$ 分以上 $80$ 分未満の生徒の人数を求めなさい。
解答・解説
解答$4$(人)
表から,B 中学校の「 $60$ 分以上 $80$ 分未満の階級」の相対度数は $0.20$ です。
B 中学校の生徒数の合計は $20$ 人だから,
「 $60$ 分以上 $80$ 分未満の階級」の度数は $\;\;20 \times 0.20=4\;\;$ です。
(3)A 中学校と B 中学校の家庭学習時間について述べた文として正しいものを,ア ~ エ から全て選び,記号で書きなさい。
アA 中学校は,B 中学校より,最頻値が大きい。
イA 中学校は,B 中学校より,中央値が小さい。
ウA 中学校は,B 中学校より,$60$ 分以上 $80$ 分未満の生徒の人数が多い。
エA 中学校は,B 中学校より,$60$ 分未満の生徒の人数が少ない。
解答・解説
ー
解答ア,ウ
アA 中学校は,B 中学校より,最頻値が大きい。
最頻値は度数(または相対度数)が最も大きい階級の階級値です。
A 中学の最頻値は (1) から,$130$ です。
表から,B 中学校の相対度数が最も大きい階級は「$100$ 分以上 $120$ 分未満の階級」で,
その階級値は $\;\;\dfrac{\;100+120\;}{2}=110\;\;$ です。
よって,A 中学校は,B 中学校より,最頻値が大きい(正しい)。
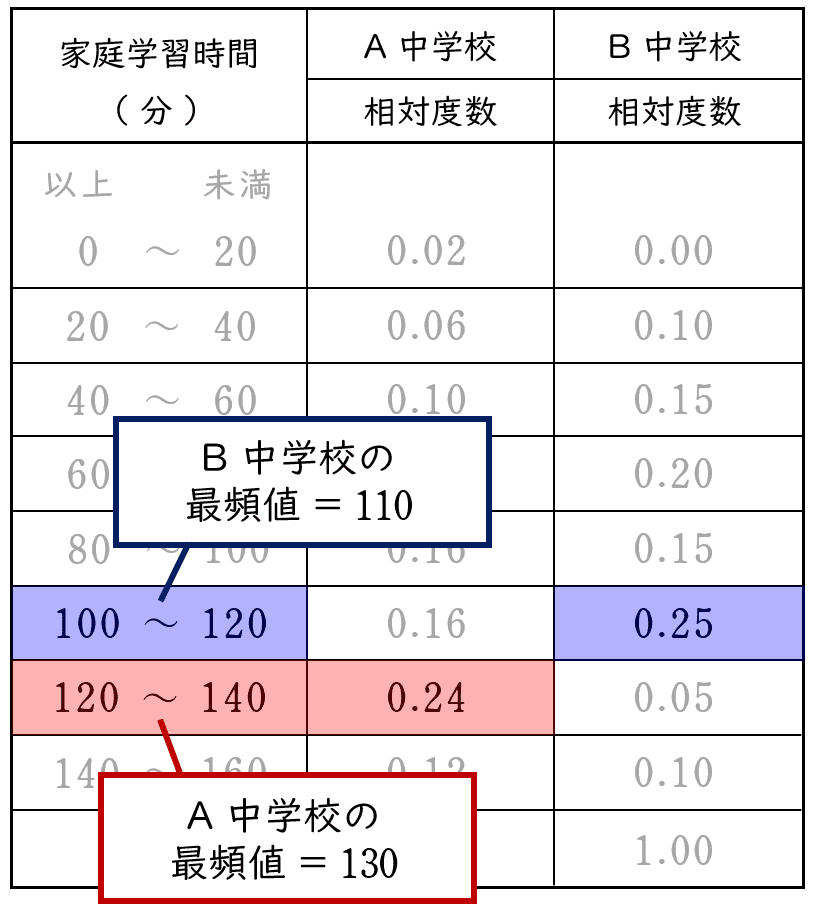
イA 中学校は,B 中学校より,中央値が小さい。
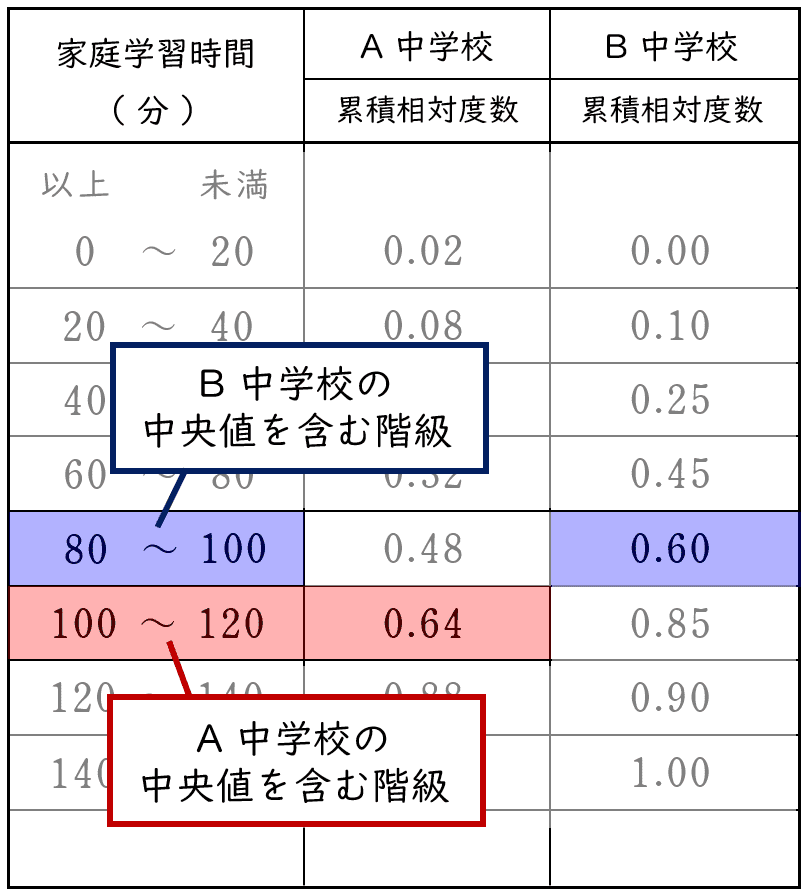
中央値は累積度数が度数の合計の半数を初めて超えた階級に含まれる,
または,
中央値は累積相対度数が 0.50 を初めて超えた階級に含まれます。
A 中学校の累積相対度数が $0.50$ を初めて超えた階級は
「$100$ 分以上 $120$ 分未満の階級」
B 中学校の累積相対度数が $0.50$ を初めて超えた階級は
「$80$ 分以上 $100$ 分未満の階級」
よって,A 中学校は,B 中学校より,中央値が大きい(正しくない)。
ウA 中学校は,B 中学校より,$60$ 分以上 $80$ 分未満の生徒の人数が多い。
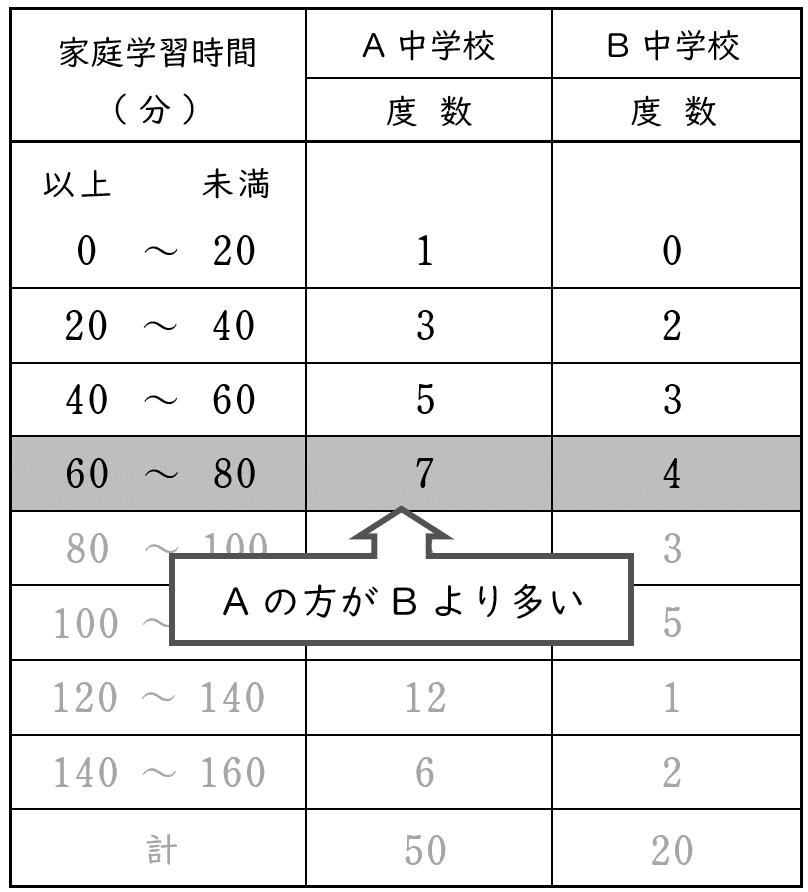
下の表は相対度数を度数に変換した度数分布表です。
表から,
A 中学校は,B 中学校より,$60$ 分以上 $80$ 分未満の生徒の人数が多い(正しい)。
エA 中学校は,B 中学校より,$60$ 分未満の生徒の人数が少ない。
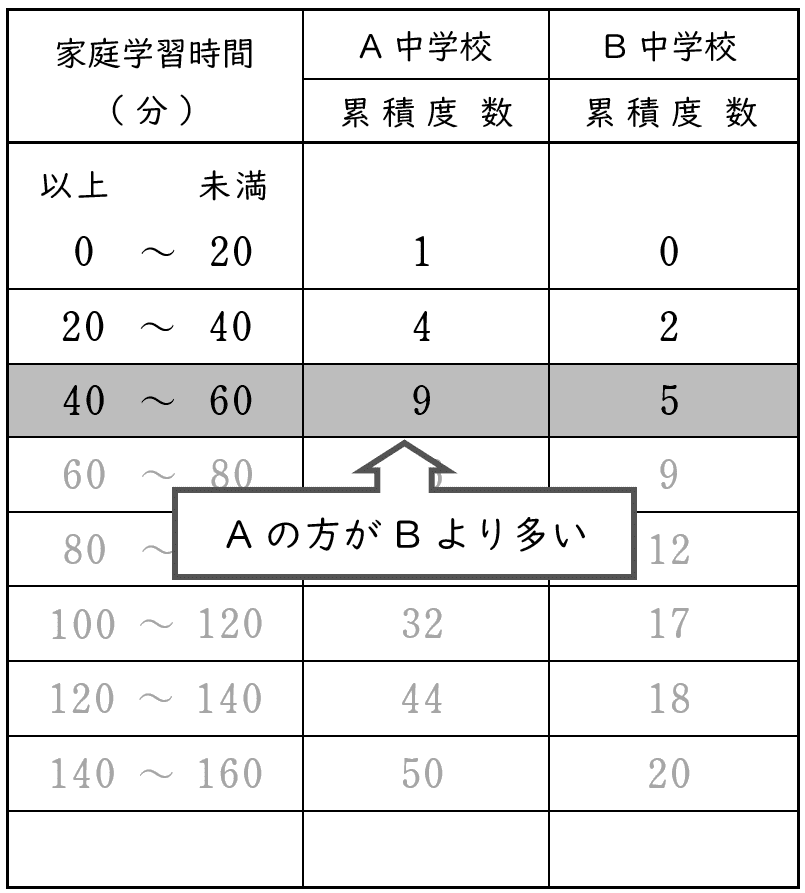
$60$ 分未満の生徒の人数は,
$60$ 分未満までの全ての階級の度数の合計(累積度数)です。
表から,
A 中学校は,B 中学校より,$60$ 分未満の生徒の人数が多い(正しくない)。
4ある作業場では,大小 $2$ 種類の電気器具 A,B を蓄電池につないで使う。蓄電池は $1600 \rm \; Wh$ まで充電でき,A,B を使うと蓄電池の残量は,それぞれ毎時一定の割合で減少する。A のみを使うとき,蓄電池の残量は $8$ 時間で $1600 \rm \; Wh$ から $0 \rm \; Wh$ になる。
作業初日,$1600 \rm \; Wh$ まで充電した蓄電池に,A をつないで使い始め,$5$ 時間後に A を B に切り換えると,A を使い始めてから $13$ 時間後に蓄電池の残量は $0 \rm \; Wh$ になった。
A を使い始めてから $x$ 時間後の蓄電池の残量を $y \rm \; Wh$ とすると,$x$ と $y$ の関係は下の表のようになった。

次の (1) ~ (4) の問いに答えなさい。
(1)表中の ア,イ に当てはまる数を求めなさい。
解答・解説
解答ア$\;\;600\quad$イ$\;\;300$
〔 ア 〕
$0≦x≦5$ の範囲では A のみを使い,電力量は毎時間一定の割合で消費され(減少し)ます。
問題文から,A は $8$ 時間で $1600 \rm \; Wh$ の電力量を消費するので,
A が $1$ 時間に消費する電力量は $1600 \div 8=200 \rm \; (Wh)$
よって,A が $5$ 時間で消費する電力量は $200 \times 5=1000\rm \; (Wh)$
したがって,ア に当てはまる数は $1600-1000=600$
〔 イ 〕
$5≦x≦13$ の範囲では B のみを使い,電力量は毎時間一定の割合で消費されます。
上で求めた通り,$5$ 時間後には $600 \rm \; Wh$ 残っており,これが $13$ 時間後に $0 \rm \; Wh$ になります。
つまり B は $(\,13-5=\,)\;8$ 時間で $600 \rm \; Wh$ の電力量を消費するので,
B が $1$ 時間に消費する電力量は $600 \div 8=75 \rm \; (Wh)$
$5$ 時間後から $9$ 時間後までは $(\,9-5=\,)\;4$ 時間で,
その間に消費される電力量は $75 \times 4=300 \rm \; (Wh)$
よって,イ に当てはまる数は $600-300=300$
(2)$x$ の変域を次の (ア),(イ) とするとき,$y$ を $x$ の式で表しなさい。
(ア) $\;\;\;0≦x≦5\;$ のとき
(イ) $\;\;\;5≦x≦13\;$ のとき
解答・解説
解答(ア)$\;\;y=-200x+1600\;\;$,(イ)$\;\;y=-75x+975\;\;$
(ア)$0≦x≦5$ のとき
$0≦x≦5$ の範囲では,消費する(減少する)電力量は一定なので,
蓄電池の残量 ($y$) は,使い始めてからの時間 ($x$) の $1$ 次関数になります。
よって,$x$ と $y$ の関係は $y=ax+b$ で表されます。
$\begin{array}{c|ccc}\;\;x &\; 0 & \cdots & 5\;\;\, \\ \hline \;\;y & \;1600 & \cdots & 600\;\; \ \end{array}$
表から変化の割合($a$)を求めます。
$a=\dfrac{\;600-1600\;}{5-0}=\dfrac{\;-1000\;}{5}=-200$
よって,求める式は $\;y=-200x+b\;$ となり,この式に $x=0$,$y=1600$ を代入して,
$1600=-200 \times 0 +b$
$\quad \;\; b=1600$
したがって,求める式は,
$y=-200x+1600$ $\;(\,0≦x≦5\,) $
(イ)$5≦x≦13$ のとき
$5≦x≦13$ の範囲では,消費する(減少する)電力量は一定なので,
蓄電池の残量 ($y$) は,使い始めてからの時間 ($x$) の $1$ 次関数になります。
よって,$x$ と $y$ の関係は $y=ax+b$ で表されます。
$\begin{array}{c|ccc}\;\;x &\; 5 & \cdots & 13\;\;\, \\ \hline \;\;y & \;600 & \cdots & 0\;\; \ \end{array}$
表から変化の割合($a$)を求めます。
$a=\dfrac{\;0-600\;}{13-5}=\dfrac{\;-600\;}{8}=-75$
よって,求める式は $\;y=-75x+b\;$ となり,この式に $x=13$,$y=0$ を代入して,
$0=-75 \times 13 +b$
$b=975$
したがって,求める式は,
$y=-75x+975$ $\;(\,5≦x≦13\,) $
(3)$x$ と $y$ の関係を表すグラフをかきなさい。$(\,0≦x≦13\,)$
解答・解説
解答
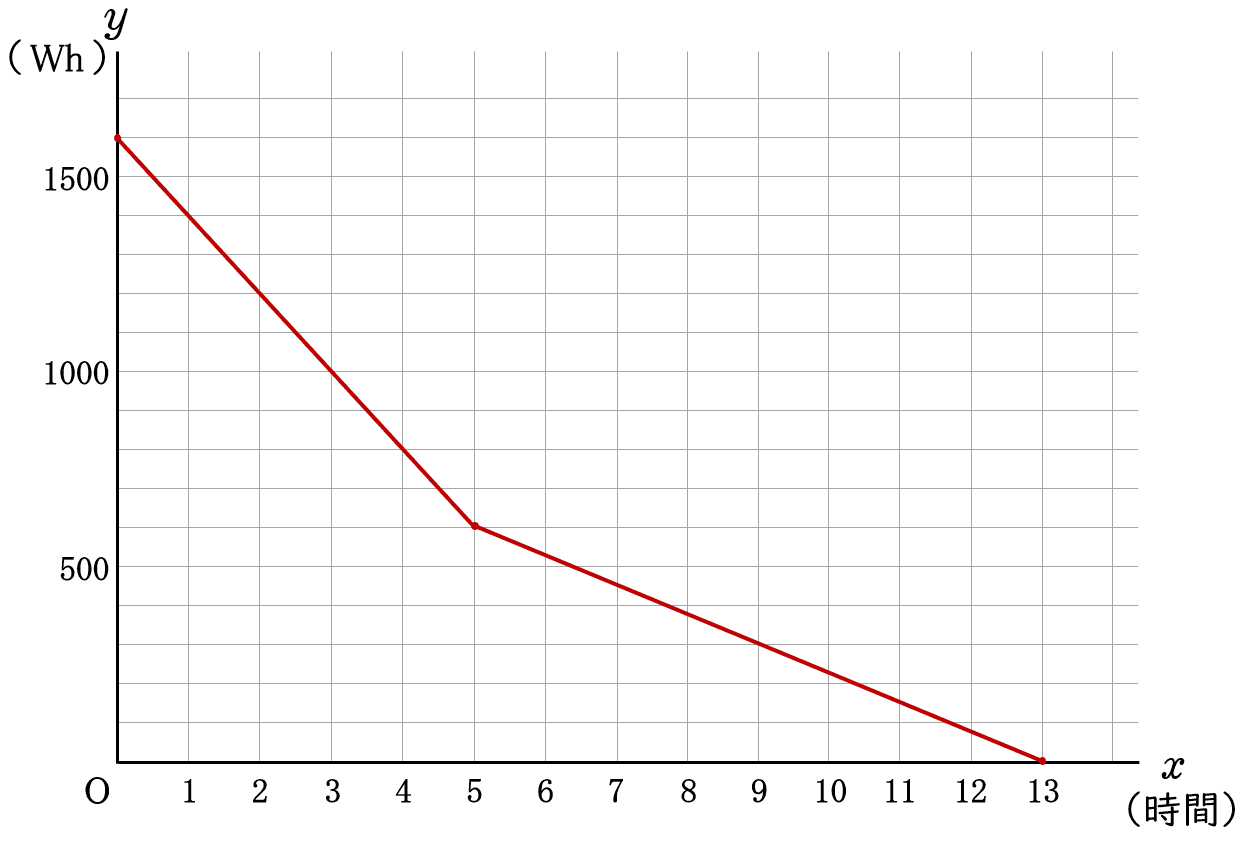
$0≦x≦5$ では,直線 $\;\;y=-200x+1600$
$5≦x≦13$ では,直線 $\;\;y=-75x+975$
(4)この作業場では,毎日,A,B を合計 $11$ 時間は使う必要がある。作業初日に,A を使う時間をできる限り長くするためには,A を使い始めてから何時間何分後に,A を B に切り換えると良かったかを求めなさい。
解答・解説
解答$24$ 秒後
問題文の「A,B を合計 $11$ 時間は使う必要がある」とは,
「A,B を合計 $11$ 時間以上使う必要がある」という意味です。
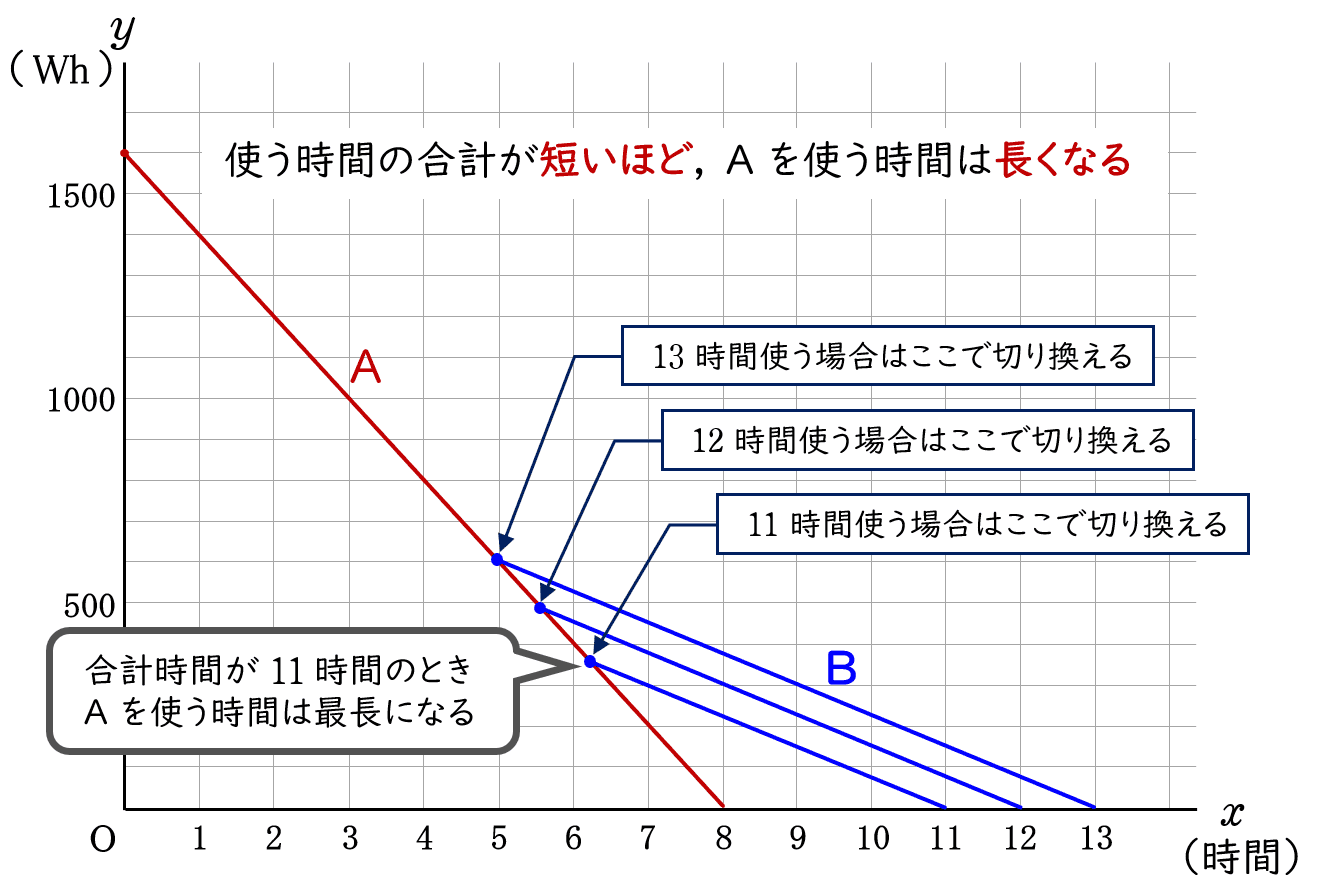
いつ 切り換えても B の $1$ 時間に消費する電力量(グラフの傾きは)は変わらないので
合計時間が短いほど A を使う時間は長くなります(下図)。
よって,A を使う時間をできる限り長くする場合の合計時間は $11$ 時間です。
解法1 【 方程式で解く場合 】
A を使い始めてから $a$ 時間後に B に切り換えたとすると,B 使用時間は $(\,11-a\,)$ 時間です。
(1) から,A,B の $1$ 時間に消費する電力量はそれぞれ $200 \rm \; Wh$,$75 \rm \; Wh$ で,合計 $1600 \rm \; Wh$ を消費するので,
$\begin{eqnarray}200a+75(\,11-a\,)&=&1600\\[5pt]a&=&\dfrac{\;31\;}{\;5\;}\;(時間)\\[5pt]&=&6\;(時間)+\dfrac{\;1\;}{\;5\;}\;(時間)\\[5pt]&=&6\;(時間)+\;12\;(分)\end{eqnarray}$
よって,$6$ 時間 $12$ 分後です。
解法2 【 関数で解く場合 】
A を B に切り換える前のグラフの式は,(2) から $\;\;y=-200x+1600\;\;$ です。
切り換えた後のグラフの傾きは,(2) から $-75$ なので,
$\;y=-75x+b\;$ に $\;x=11$,$y=0\;$ を代入して,
$0=-75 \times 11 +b$
$b=825$
よって,切り換えた後のグラフの式は $\;\;y=-75x+825\;\;$です。
切り換えた時間は,次の連立方程式から求めることができます。
$\begin{eqnarray}\;\;\left\{\begin{array}{l}\;y=-200x+1600&\cdots①& \\[5pt]\;y=-75x+825 &\cdots②& \end{array}\right.\end{eqnarray}\;\;$
①,② から,
$\begin{eqnarray}-200x+1600&=&-75x+825\\[5pt]-125x&=&-775\\[5pt]x&=&\dfrac{\;31\;}{\;5\;}\;(時間)\\[5pt]&=&6\;(時間)+\dfrac{\;1\;}{\;5\;}\;(時間)\\[5pt]&=&6\;(時間)+\;12\;(分)\end{eqnarray}$
よって,$6$ 時間 $12$ 分後です。
5下の図で, △ABC は ∠ABC = $90$° の直角二等辺三角形であり,△BDC は ∠BDC = $90$° の直角三角形である。また,点 E は辺 DC を延長した直線上の点で,BD = CE である。
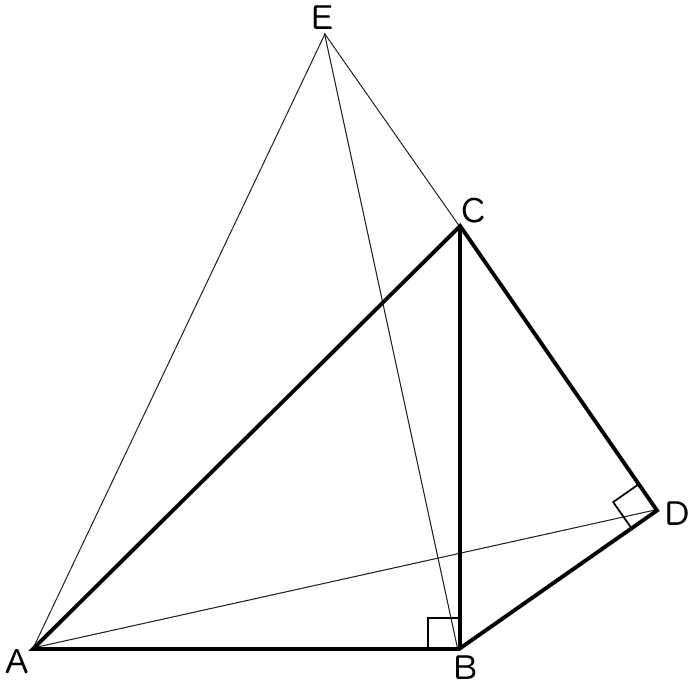
次の (1),(2) の問いに答えなさい。
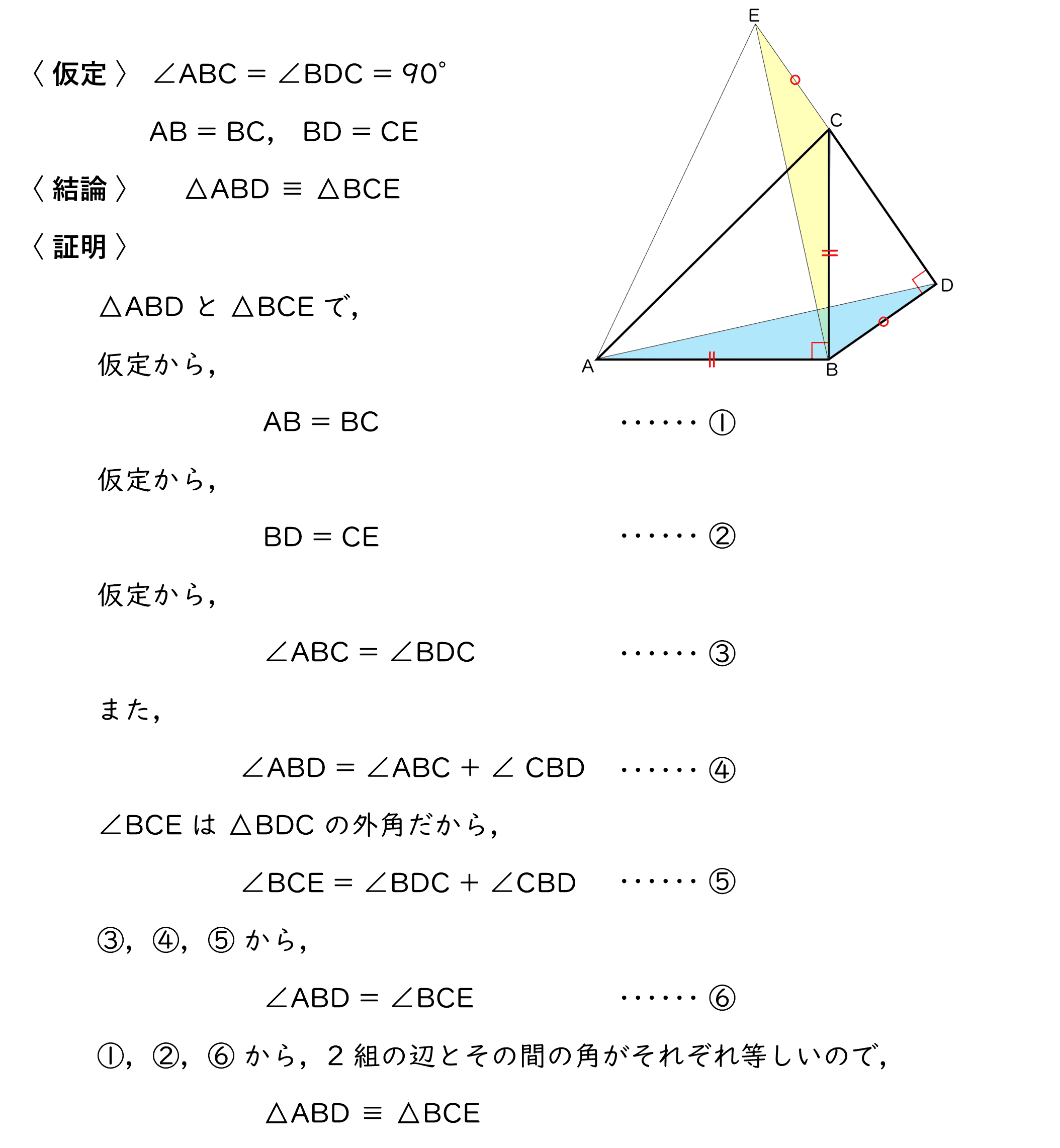
(1)△ABD ≡ △BCE であることを証明しなさい。
解答
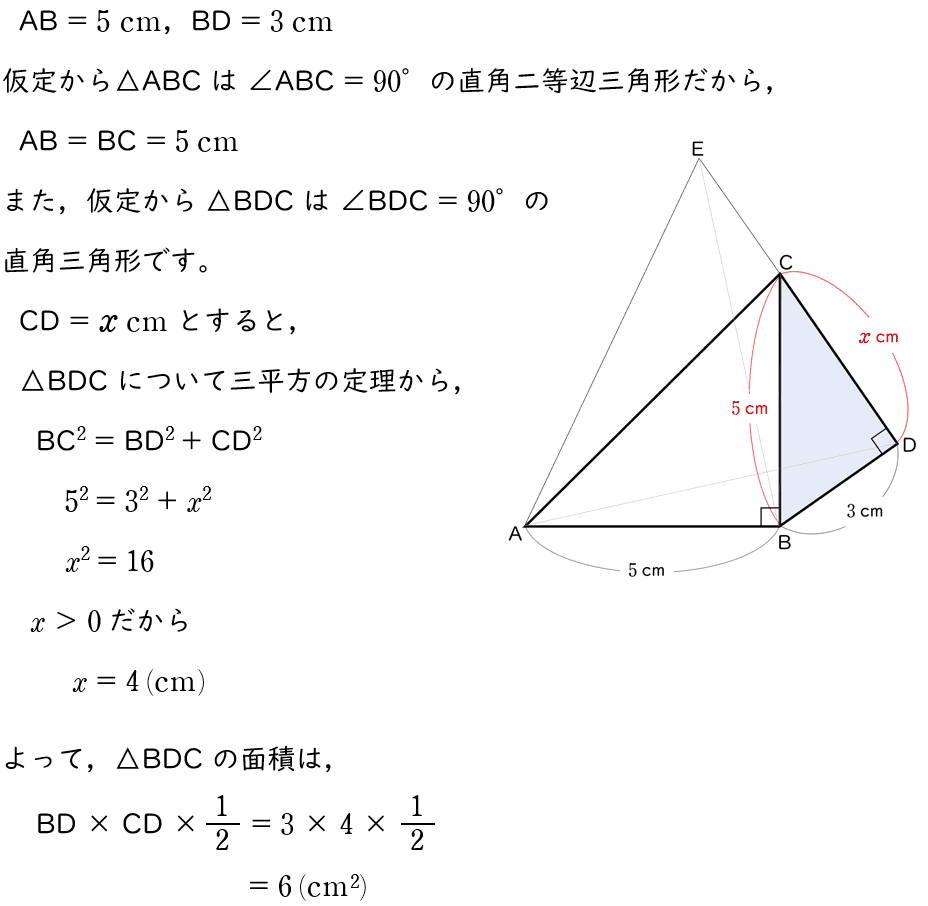
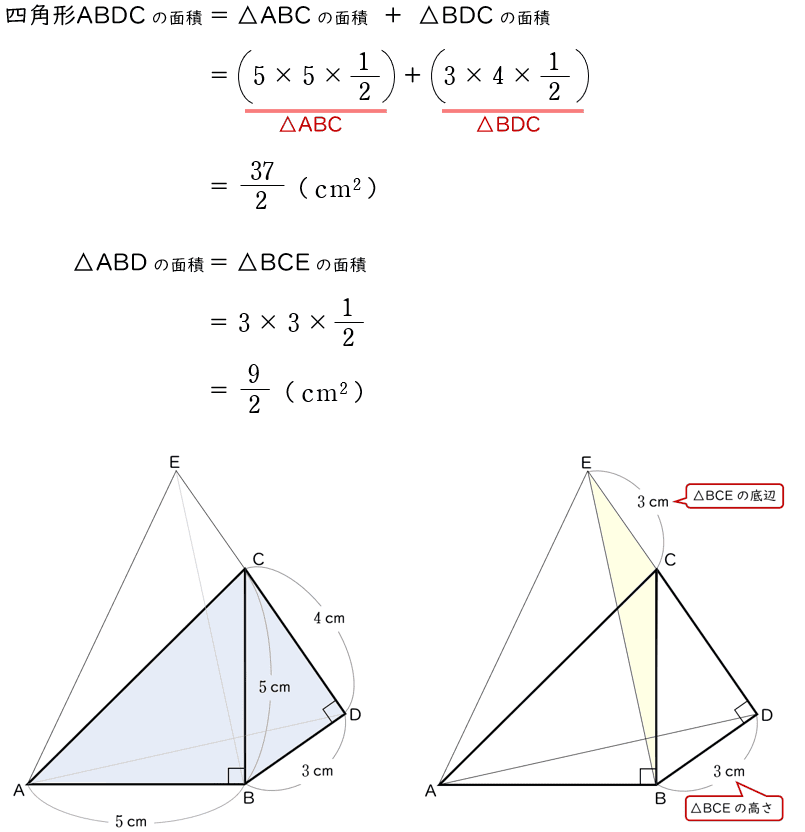
(2)AB $=5\;\rm cm$,BD $=3\;\rm cm$ のとき,
(ア)△BDC の面積を求めなさい。
解答・解説
解答$6\;\rm cm^2$
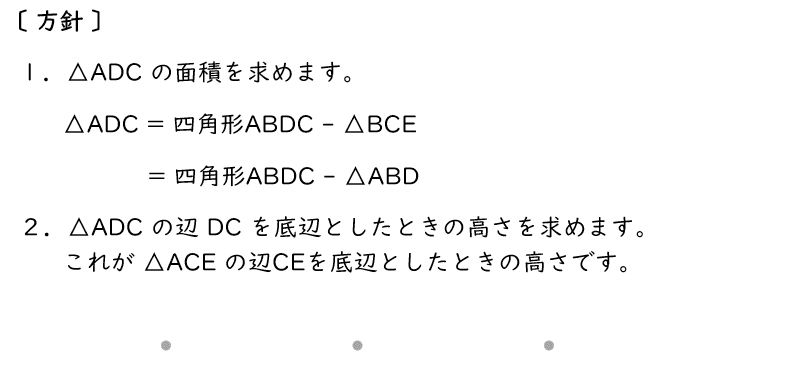
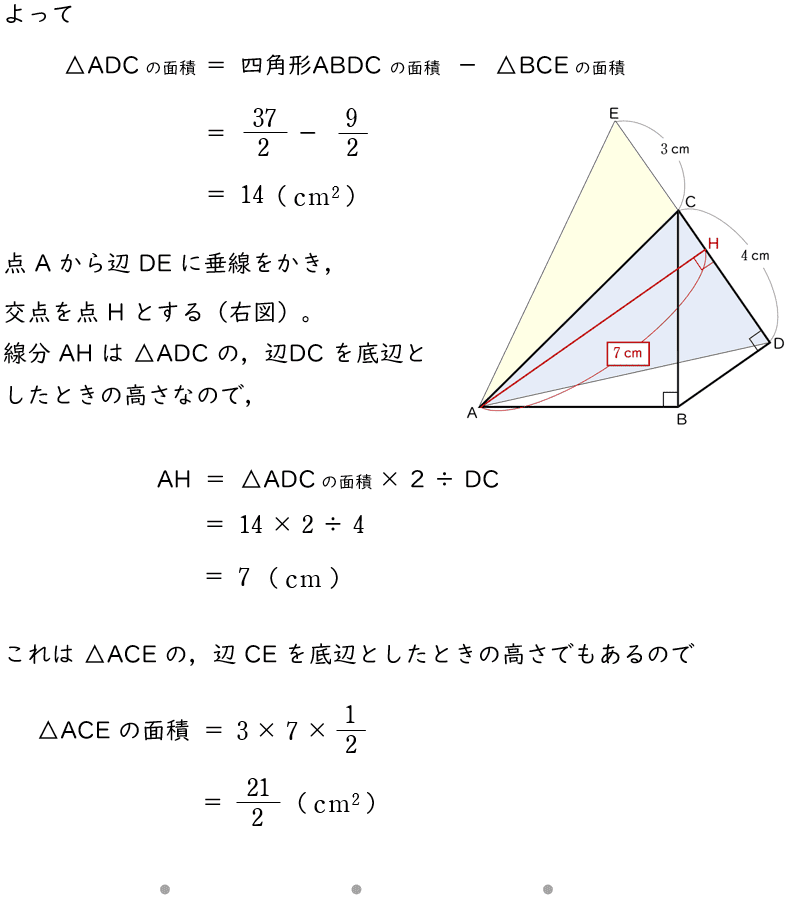
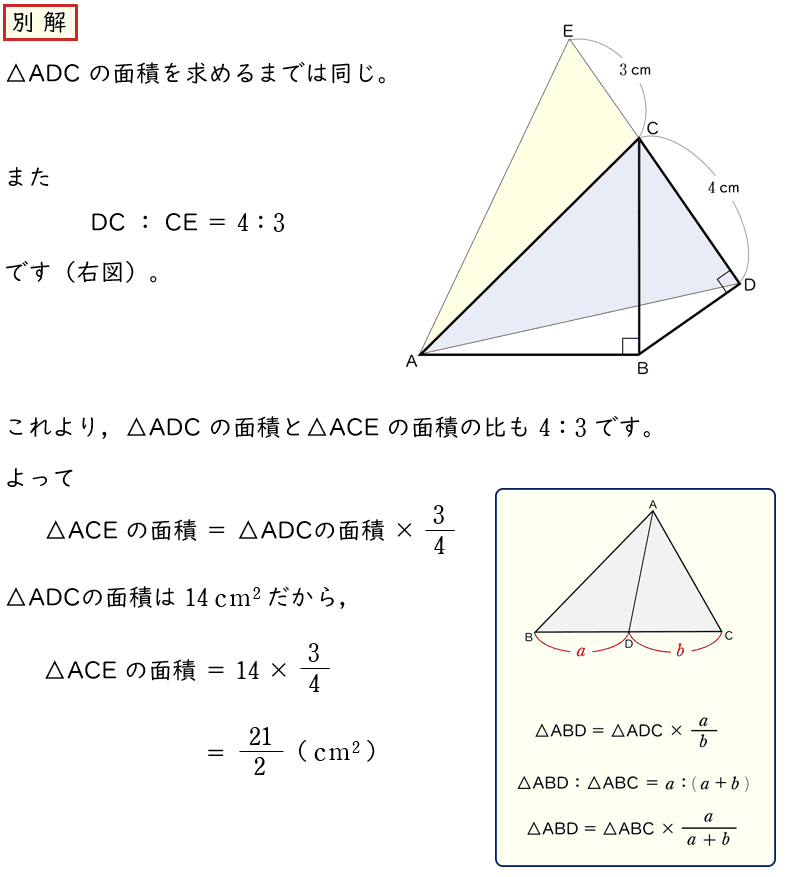
(イ)△ACE の面積を求めなさい。
解答・解説
解答$\dfrac{\;21\;}{\;2\;}\;\;\rm cm^2$
6図 1 のように,白色の面に $1$ から $6$ までの自然数が $1$ つずつ書かれた $6$ 枚のカードがある。これらのカードの反対側の面は灰色で,白色の面と同じ自然数が書かれている。また,図 2 のように,袋の中に赤玉,青玉,黄玉がそれぞれ $1$ 個ずつ入っている。
全てのカードの白色の面を上にしてから,次の操作を繰り返し行う。
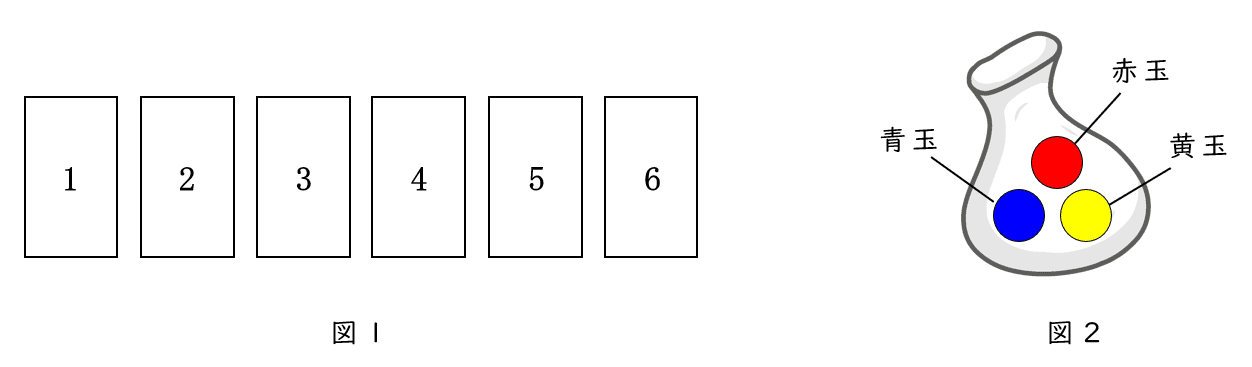
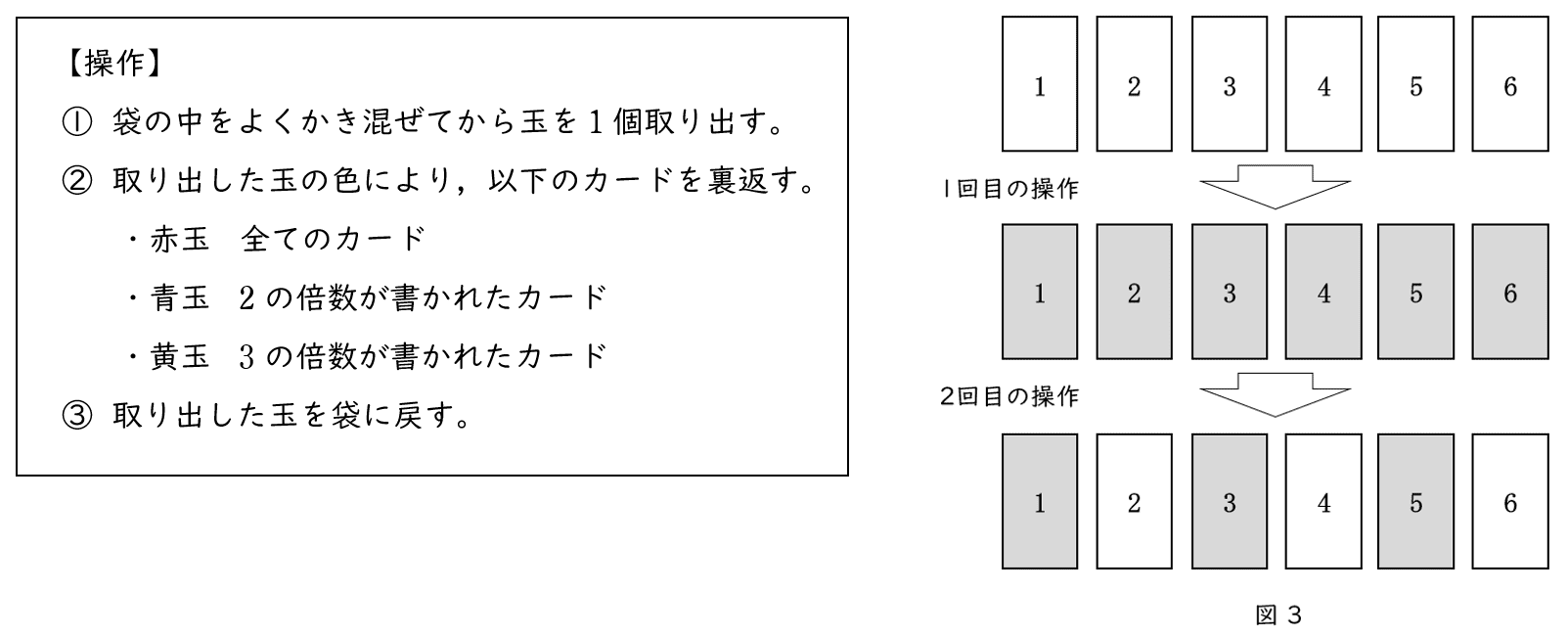
図 3 は,$1$ 回目の操作で赤玉,$2$ 回目の操作で青玉を取り出したときの,カードの上になっている面を表している。
次の (1) ~ (4) の問いに答えなさい。
(1)$10$ 回の操作で,赤玉を $5$ 回,青玉を $3$ 回,黄玉を $2$ 回取り出すとき,$2$ が書かれたカードを裏返す回数を求めなさい。
解答・解説
解答$8\;$回
$2$ が裏返されるのは,赤玉と青玉を取り出すときです。
赤玉を $5$ 回,青玉を $3$ 回取り出すので,$2$ が裏返される回数は
$5+3=8$(回)
(2)次の文章は,$10$ 回の操作で各カードを裏返す回数について,太郎さんが考えたことをまとめたものである。ア,イ には,$a$ を使った式を,ウ には $b$ を使った式を,エ には数を,それぞれ当てはまるように書きなさい。
$10$ 回の操作で,赤玉を取り出す回数を $a$ 回,青玉を取り出す回数を $b$ 回とすると,黄玉を取り出す回数は( ア ) 回と表すことができる。このとき,各カードを裏返す回数は下の表のようになる。

解答・解説
解答ア$\;\;10-a-b$,$\quad$イ$\;\;a+b$,$\quad$ウ$\;\;10-b$,$\quad$エ$\;\;10$
〔 ア 〕
$10$ 回の操作で,赤玉を $a$ 回,青玉を $b$ 回取り出すので,
黄玉を取り出す回数は
$10-(a+b)=10-a-b$(回)… ア$10-a-b$
| 取り出す玉 裏返すカード |
赤 玉 すべて |
青 玉 2 の倍数 |
黄 玉 3 の倍数 |
|---|---|---|---|
| 取り出す回数 | $a$ | $b$ | $10-a-b$ |
〔 イ 〕
$2$ を裏返すのは,赤玉と青玉を取り出すときだから
$a+b$(回)… イ$a+b$
〔 ウ 〕
$3$ を裏返すのは,赤玉と黄玉を取り出すときだから
$a+(10-a-b)=10-b$(回)… ウ$10-b$
〔 エ 〕
$6$ は $2$ と $3$ の公倍数です。
よって,$6$ はどの色の球を取り出しても裏返すので,その回数は
$a+b+(10-a-b)=10$(回)… エ$10$
〔 完成した表 〕
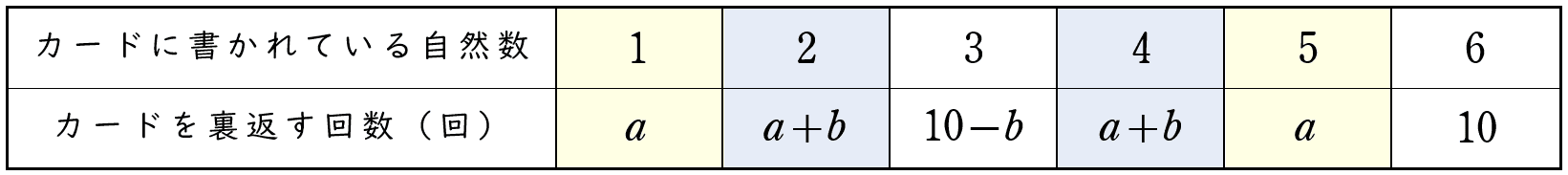
$1$ と $5$ の組,$2$ と $4$ の組はそれぞれ裏返す回数が同じなので,いつも同じ色の面が上になります。
(3)$10$ 回の操作を行った後,白色の面が上になっているカードが $2$ 枚であるとき,その $2$ 枚のカードに書かれている自然数を両方とも書きなさい。
解答・解説
解答$3$,$6$
白色面が上になっているカードは,偶数回裏返されたものです。
$6$ はどの色の球が取り出されても裏返すので,$10$ 回操作を行った後,白色面が上になっています。
そこで,$6$ 以外にあと $\color{#8b0000}{1}$ 枚だけ白色になる場合を考えます。
(2) の表(下表)から,$1$ と $5$ の組,$2$ と $4$ の組はそれぞれ同じ回数裏返すので,これらの組を偶数回裏返すと $6$ 以外に $2$ 枚以上 ,すなわち合計 $3$ 枚以上のカードの白色面が上になります。
よって,$6$ 以外に $1$ 枚だけ白色面が上になる場合があるのは $3$ だけです。
したがって,$10$ 回操作を行った後,白色面が上になる $2$ 枚は $3$ と $6$ です。
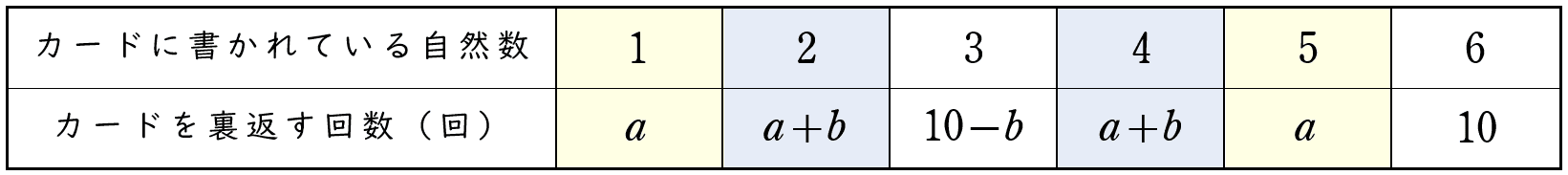
$1$ と $5$ の組,$2$ と $4$ の組はそれぞれ裏返す回数が同じなので,いつも同じ色の面が上になります。
(4)$10$ 回の操作を行った後,各カードの上になっている面の色を下の表に記録する。この記録によってできる表は,全部で何通りあるかを求めなさい。

解答・解説
解答$4\;$通り
$6$ は必ず白面が上になっているので,$1$ 〜 $5$ について考えればよい。
また、$1$,$5$ の組,$2$,$4$ の組はそれぞれ同じ面が上になっています。
したがって,$1$ $5$ の組 と $2$ $4$ の組 と $3$ の色について調べます。
$10$ 回の操作を行った後,$a$,$b$,$a+b$,$10-b$ それぞれが偶数または奇数になる組み合わせと,各カードの上になっている面の色は下の表のようになります。
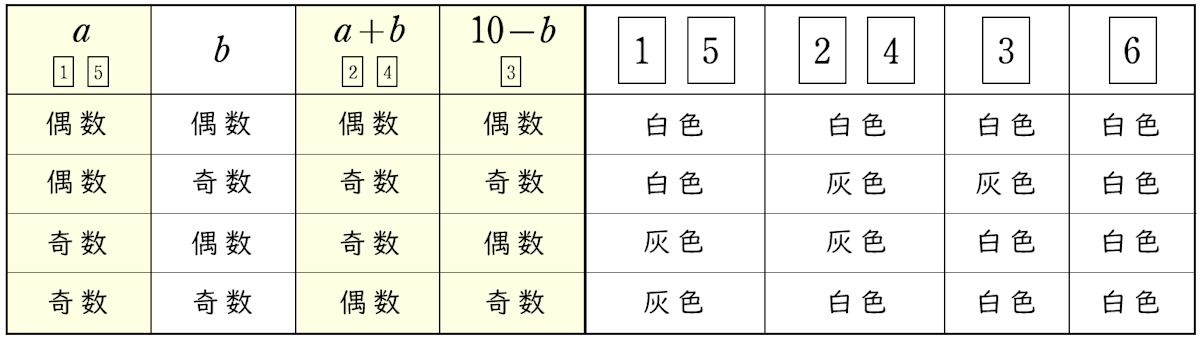
$a+b$ と $10-b$ が偶数になるか奇数になるかは,$a$ と $b$ が偶数であるか奇数であるかで決まるので,上の表以外の組み合わせはありません。
よって,記録によってできる表は,全部で $4$ 通りです。
〔 記録によってできる表 〕