岐阜県・公立高校入試 2024年度( 令和6年度 )解答・解説編
岐阜県立高校・入学試験学力検査・数学・2024年度
1次の(1)~(6)の問いに答えなさい。
(1)$8+(\,-4\,)\div 2\;\;$を計算しなさい。
解答・解説
解答$6$
$8+\color{red}(\,-4\,)\div 2 \color{black}$
$=8+(\,-2\,)$
$=8-2$
$=6$
(2)$3x+y-2(\,x-3y\,)\;\;$を計算しなさい。
解答・解説
解答$x+7y$
$3x+y-2(\,x-3y\,)$
$=3x+y-2x\color{red}+\color{black}6y$
$=3x-2x+y+6y$
$=x+7y$
(3)$\sqrt{\,3\,}+\dfrac{9}{\,\sqrt{\,3\,}\,}\;\;$を計算しなさい。
解答・解説
解答$4\sqrt{\,3\,}$
$\sqrt{\,3\,}+\dfrac{9}{\,\sqrt{\,3\,}\,}$
$=\sqrt{\,3\,}+\dfrac{\;\,9\;\;\color{red}\times \sqrt{\,3\,}}{\,\sqrt{\,3\,}\color{red}\times\sqrt{\,3\,}\,}$
$=\sqrt{\,3\,}+\dfrac{\,\color{red}\cancelto{3}{\color{black}9}\color{black}\sqrt{\,3\,}\,}{\color{red}\cancelto{1}{\color{black}3}\color{black}}$
$=\sqrt{\,3\,}+3\sqrt{\,3\,}$
$=4\sqrt{\,3\,}$
(4)$y$ が $x$ に反比例し,$x=-6$ のとき $y=10$ である。$x=-3$ のときの $y$ の値を求めなさい。
解答・解説
解答$20$
$y$ が $x$ に反比例するから,比例定数を$a$ とすると,
$\begin{eqnarray}
y &=& \dfrac{a}{\;x\;} \\ xy &=& a \end{eqnarray}$
と表せる。
この式に $x=-6$,$y=10$ を代入すると,
$\begin{eqnarray}
-6 \times 10 &=& a\\
a &=& -60
\end{eqnarray}$
よって,$\quad y=-\dfrac{60}{\;x\;}$
この式に $x=-3$ を代入すると,
$\begin{eqnarray}
y &=& -60 \div (\;-3\;)\\
&=& 20
\end{eqnarray}$
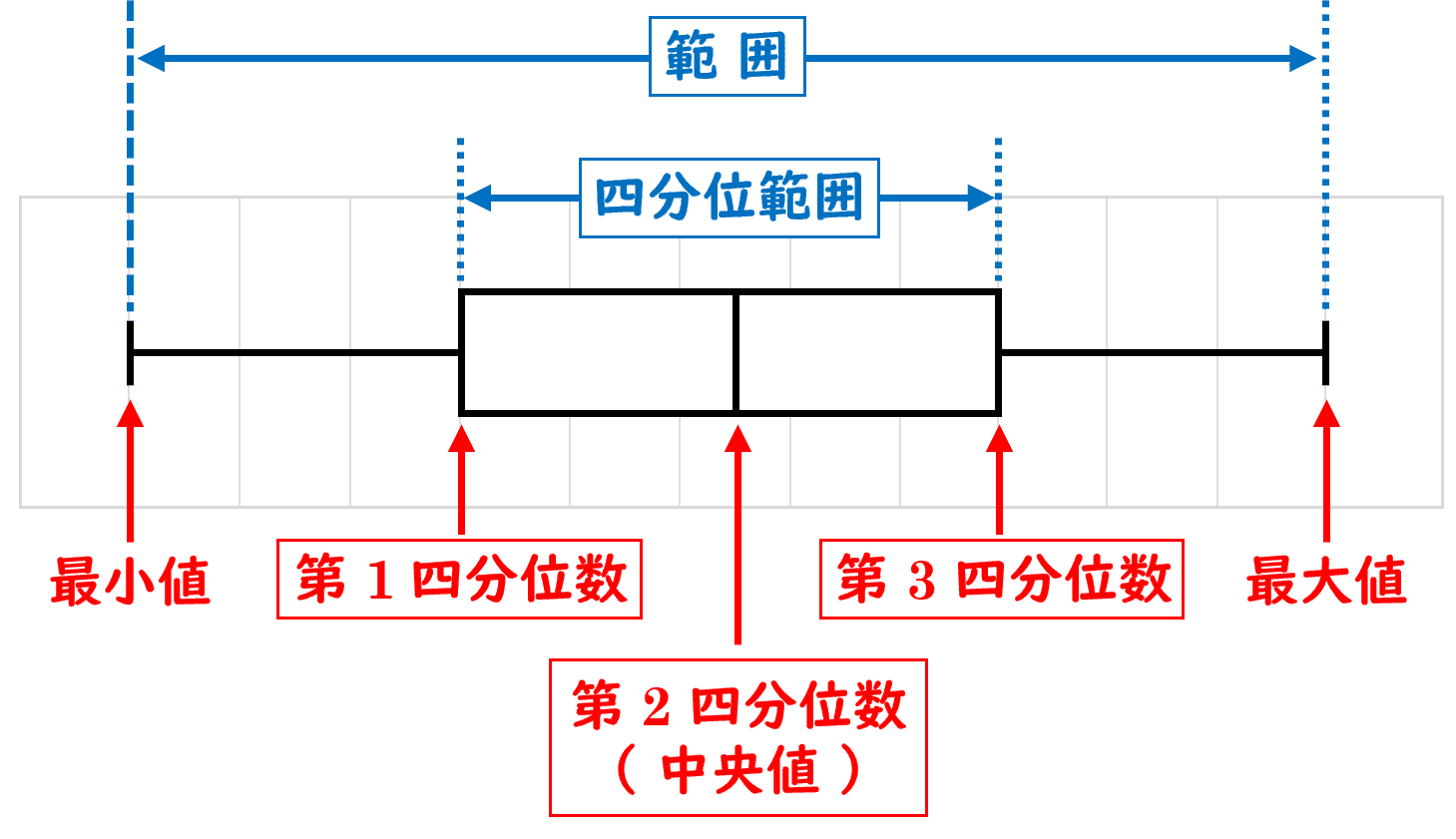
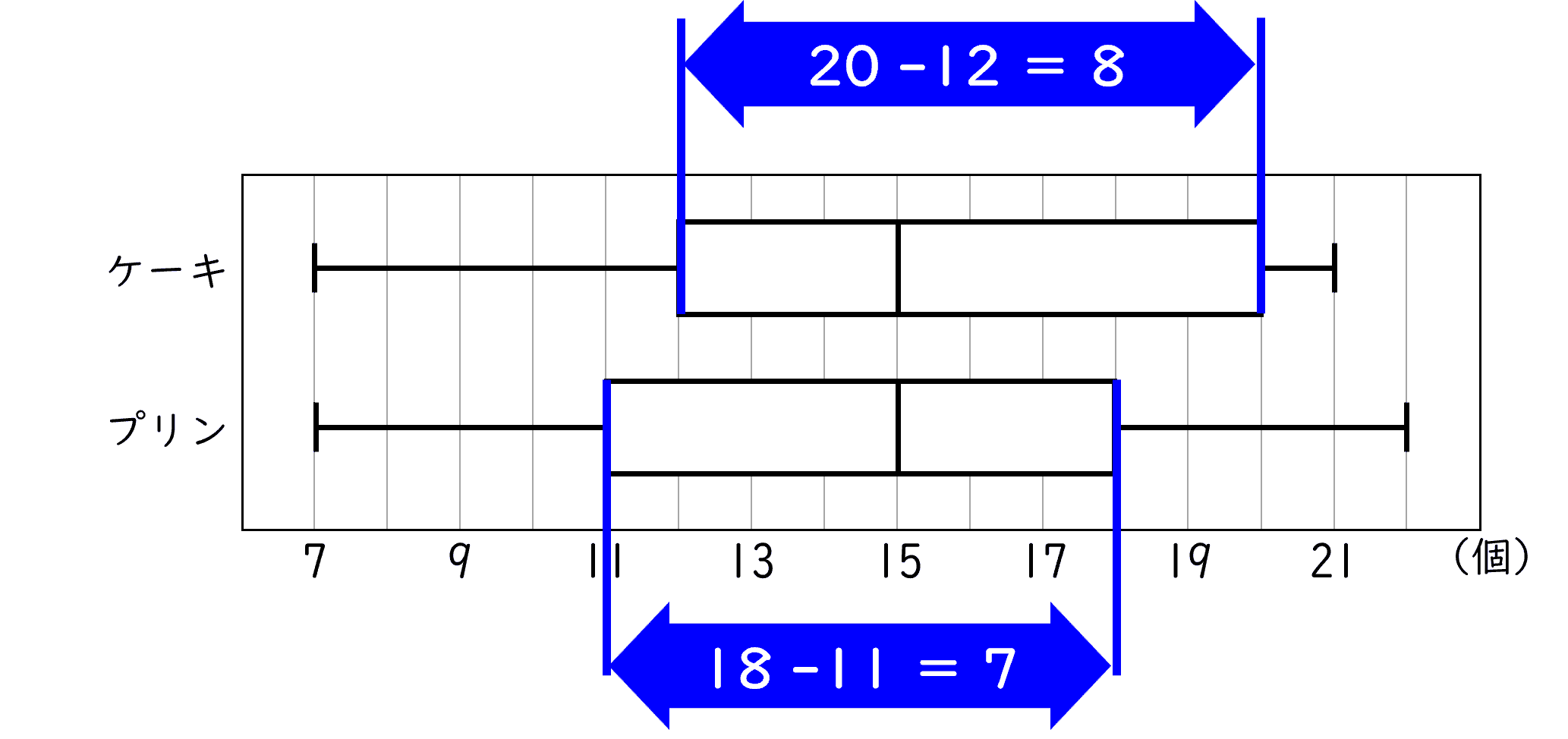
(5)ある店で,$8$ 月の $31$ 日間,毎日ケーキとプリンが売られていた。下の図は,ケーキとプリンが $8$ 月の各日に売れた個数について,それぞれのデータの分布の様子を箱ひげ図に表したものである。
この図から読み取れることとして正しいものをを,ア ~ エ から全て選び,符号で書きなさい。

アケーキとプリンでは,最大値が同じである。
イケーキとプリンでは,中央値が同じである。
ウケーキとプリンでは,プリンの方が四分位範囲は大きい。
エケーキとプリンでは,ケーキのほうが $19$ 個以上売れた日は多い。
解答・解説
ー
解答イ,エ
ア~エについて,一つずつ検討していきます。
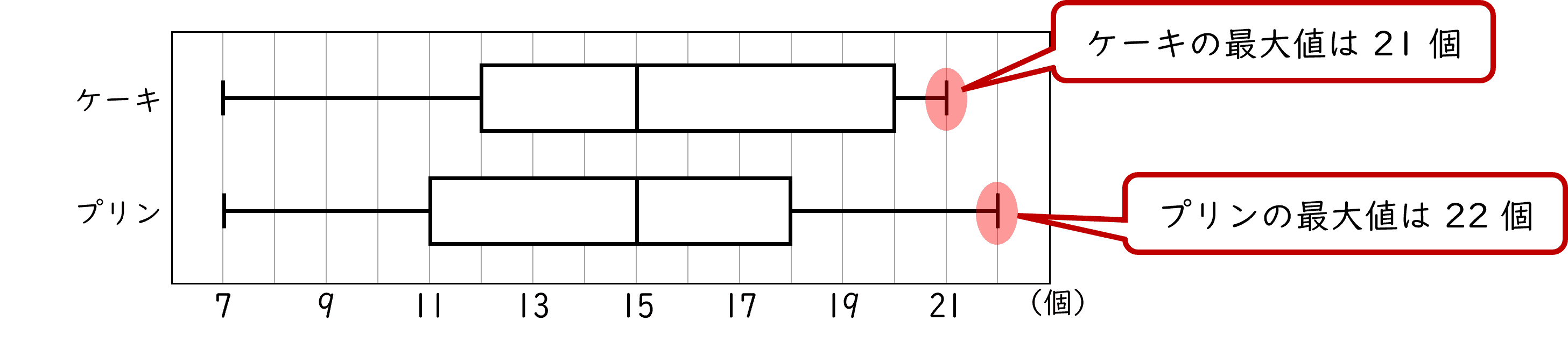
アケーキとプリンでは,最大値が同じである。
下の図の通り,ケーキとプリンでは,最大値は異なります。
よって,ア は正しくありません。
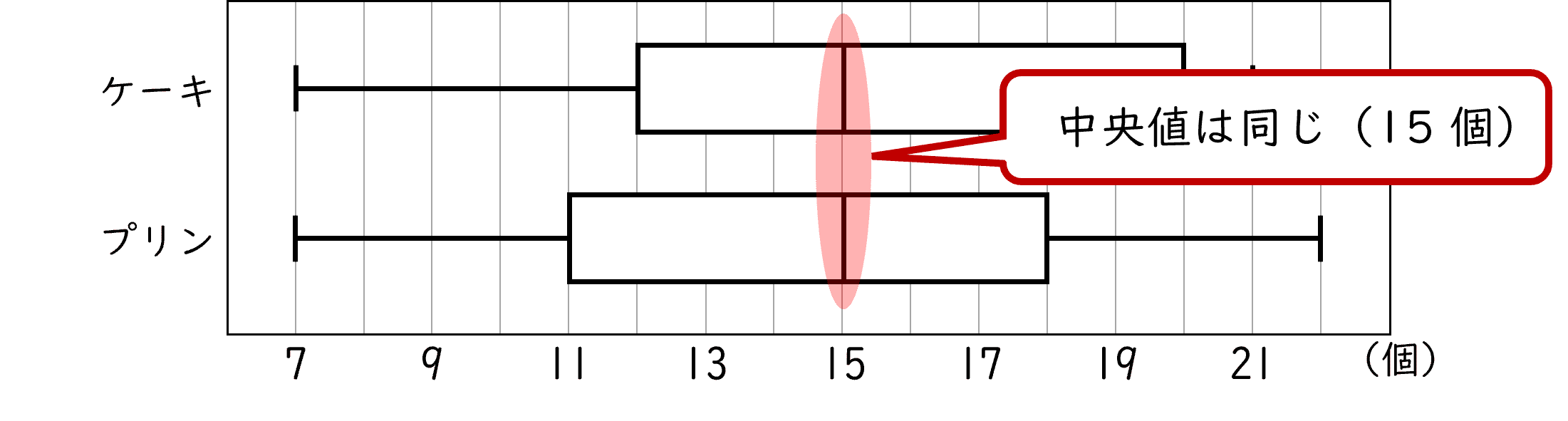
イケーキとプリンでは,中央値が同じである。
下の図の通り,ケーキとプリンでは,中央値は同じです。
よって,イ は正しいです。
ウケーキとプリンでは,プリンの方が四分位範囲は大きい。
下の図の通り,ケーキとプリンの四分位範囲はそれぞれ $8$,$7$ であり,ケーキの方が四分位範囲は大きいです。
よって,ウ は正しくありません。
エケーキとプリンでは,ケーキのほうが $19$ 個以上売れた日は多い。
下の図は,ケーキとプリンの売れた個数の中央値以上のデータの分布を表したものです。
それぞれのデータの総数は $31$ なので,中央値は大きい方から$16$ 番目,第 $3$ 四分位数は大きい方から $8$ 番目です。
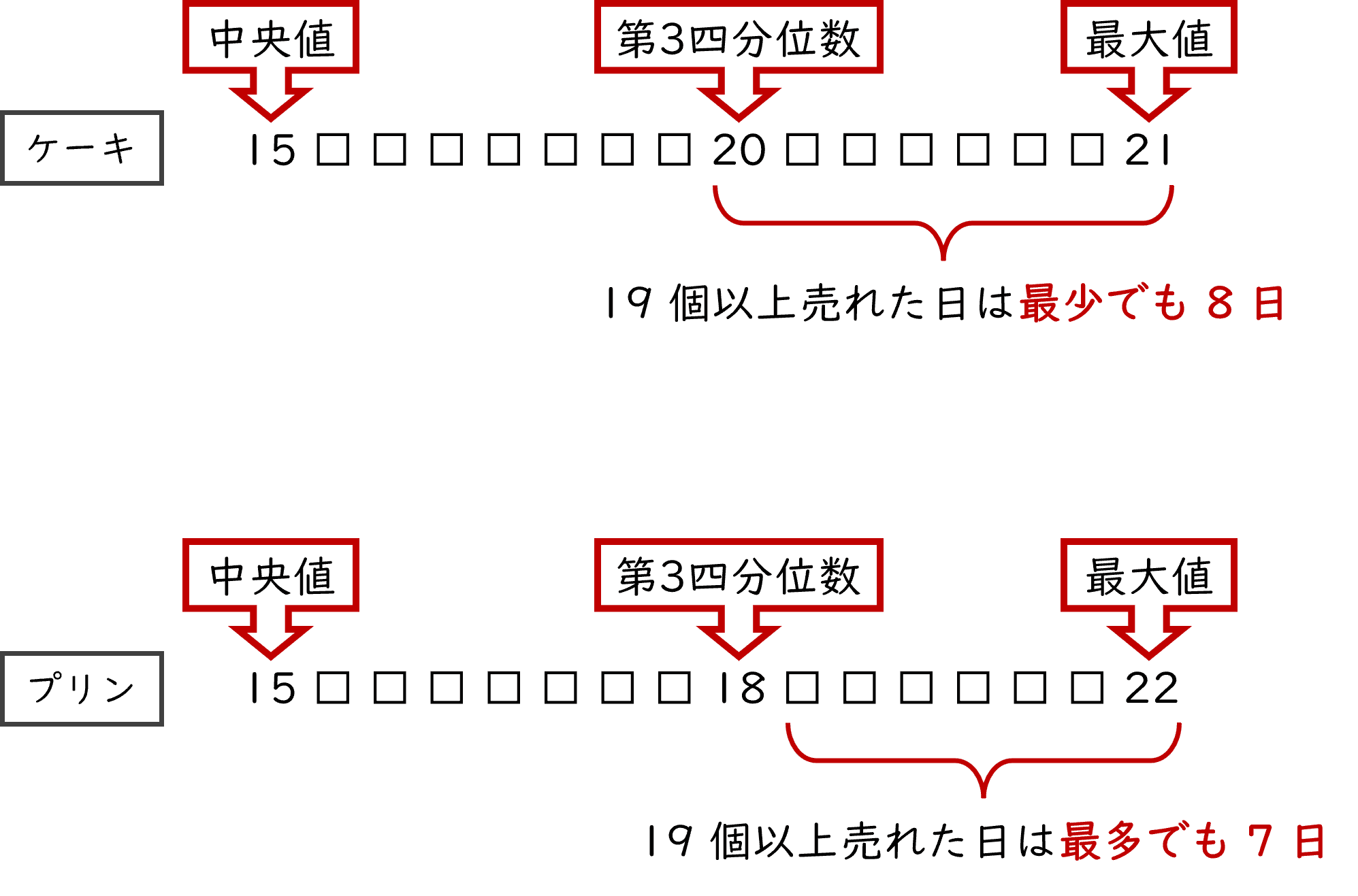
上の図から,
ケーキは $19$ 個以上売れた日は最小でも $8$ 日になります。
プリンは $19$ 個以上売れた日は最多でも $7$ 日になります。
よって,ケーキとプリンではケーキの方が $19$ 個以上売れた日は多く,エ は正しいです。
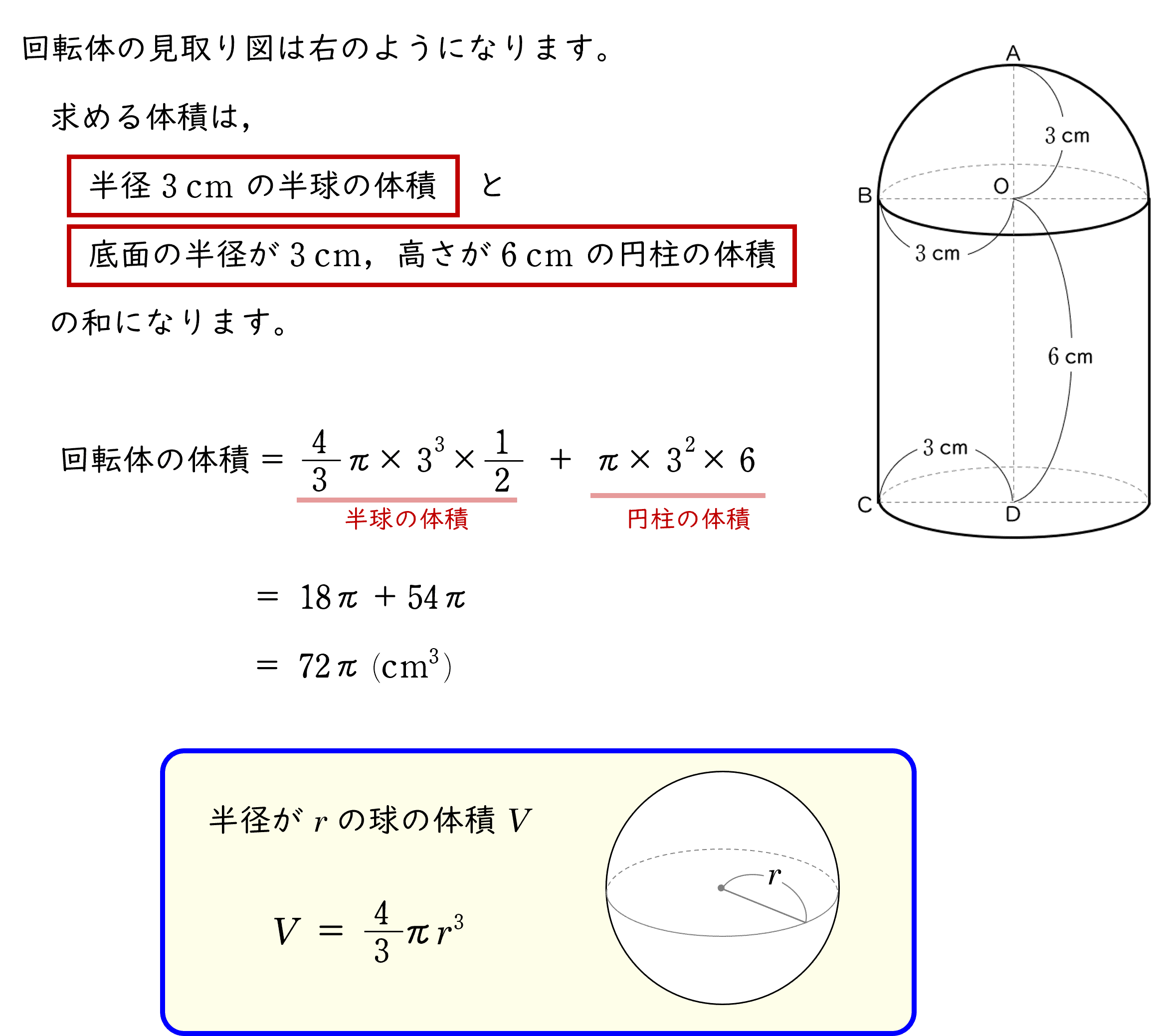
(6)下の図は,$2$ つの半径 OA,OB と 弧 AB で囲まれたおうぎ形と,長方形 OBCD を組み合わせた図形である。この図形を,直線 AD を軸として $1$ 回転させてできる立体の体積を求めなさい。

解答・解説
解答$72\pi \;\rm cm^3$
2あるパーティー会場にテーブルが何台かある。これらをすべて使い,パーティーの全ての参加者をテーブルごとに分けて座らせたい。いま,参加者をテーブルごとに $6$ 人ずつ分けると,テーブルが不足し,8 人が座れない。
次の (1) ,(2) の問いに答えなさい。
(1)パーティー会場にあるテーブルの台数を $x$ 台とするとき,参加者の人数を $x$ を使った式で表しなさい。
解答・解説
解答$6x+8$(人)
『 参加者をテーブルごとに $6$ 人ずつ分けると,テーブルが不足し,8 人が座れない』
参加者の人数 $=$ テーブルに座れる人の数 + 座れない人の数
なので,テーブルの台数を $x$ 台とすると,
テーブルに座れる人の数 $=6x$ (人)
となります。また,座れない人の数は $8$ 人なので,
参加者の人数 $=6x+8$(人)
となります。
(2)参加者をテーブルごとに $7$ 人ずつ分けると,テーブルは $2$ 台余るが,全ての参加者が $7$ 人ずつ座れる。
(ア)パーティー会場にあるテーブルは全部で何台かを求めなさい。
(2)の(ア)の解答・解説
解答$22$ 台
『 参加者をテーブルごとに $7$ 人ずつ分けると,テーブルは $2$ 台余るが,全ての参加者が $7$ 人ずつ座れる 』
参加者の人数 $=$ テーブルに座れる人の数
なので,テーブルの台数を $x$ 台とすると,参加者が座っているテーブルは $x-2$(台)で,そのすべてに $7$ 人ずつ座っているから,
参加者の人数 $=7(x-2)$(人)
となります。
また,(1) から,参加者の人数は $6x+8$(人)とも表せるので,参加者の人数について次の方程式を立てることができます。
$\begin{eqnarray}6x+8&=&7(x-2)\\[5pt]6x+8&=&7x-14\\[5pt]6x-7x&=&-14-8\\[5pt]x&=&22\end{eqnarray}$
よって,テーブルの台数は $22$ 台です。
さらに,(イ)のために,参加者の人数も求めておきます。
(1) で求めた式に,$x=22$ を代入して
参加者の人数 $=6\times 22+8=140$(人)
(イ)パーティー会場にあるテーブルを全て使い,全ての参加者をテーブルごとに $6$ 人か $7$ 人のどちらかに分けるとすると,$6$ 人のテーブルは全部で何台になるかを求めなさい。
(2)の(イ)の解答・解説
解答$14$ 台
$6$ 人のテーブルを $a$ 台,$7$ 人のテーブルを $b$ 台にするとします。
テーブルは全部で $22$ 台あるから,
$a+b=22$
$6$ 人のテーブルに座っている人は $6a$ 人,$7$ 人のテーブルに座っている人は $7b$ 人います。
また(ア)から,参加者は全部で $140$ 人いるので,
$6a+7b=140$
よって,次の連立方程式を立てることができます。
$\quad \begin{eqnarray}\;\;\left\{\begin{array}{l}\;a+b=22&\cdots①& \\[5pt]\;6a+7b=140 &\cdots②& \end{array}\right.\end{eqnarray}\;\;$
加減法で解きます。
$\begin{eqnarray}①\times 7\,\;\;\;\;\;\;\;\;7a+7b&=&154\\[3pt]②\,\;\;\;\;\;\;\;\; -) \;\;6a+7b&=&140\\[3pt]\hline a\;\;\;\;\;\;\;\;&=&14\end{eqnarray}$
よって,$6$ 人のテーブルは $14$ 台です。
3下の図のような正三角形 ABC があり,点 P は頂点 A の位置にある。また,$0$ から $4$ までの数字が $1$ つずつ書かれた $5$ 枚のカード$0$$1$$2$$3$$4$ が,袋の中に入っている。
次の操作を $2$ 回行う。
$\;$【操作】
袋からカードを $1$ 枚取り出し,そのカードに書かれた数字の数だけ,P を正三角形の頂点から頂点へ左回りに移動させる。P を移動させた後,取り出したカードを袋に戻す。

例えば,$1$ 回目に $2$ のカードを,$2$ 回目に $0$ のカードを取り出したとき,$1$ 回目の操作後に P は頂点 C にあり,$2$ 回目の操作後も P は頂点 C にある。
次の (1) ~ (3) の問いに答えなさい。
(1)$1$ 回目の操作後に P が頂点 A にある確率を求めなさい。
解答・解説
解答$\dfrac{2}{\,5\,}$
$1$ 回目の操作で,カードの取り出し方は $5$ 通りあります。
そのうち,P が頂点 A にあるのは,$0$ のときと,$3$ のときの $2$ 通りです。
よって,$1$ 回目の操作後に P が頂点 A にある確率は
$\dfrac{2}{\,5\,}$
です。
(2)$1$ 回目の操作後に P が頂点 A にあり,$2$ 回目の操作後も P が頂点 A にある確率を求めなさい。
解答・解説
解答$\dfrac{4}{\;25\;}$
操作を $2$ 回行ったときの,P の動き方を表にします。
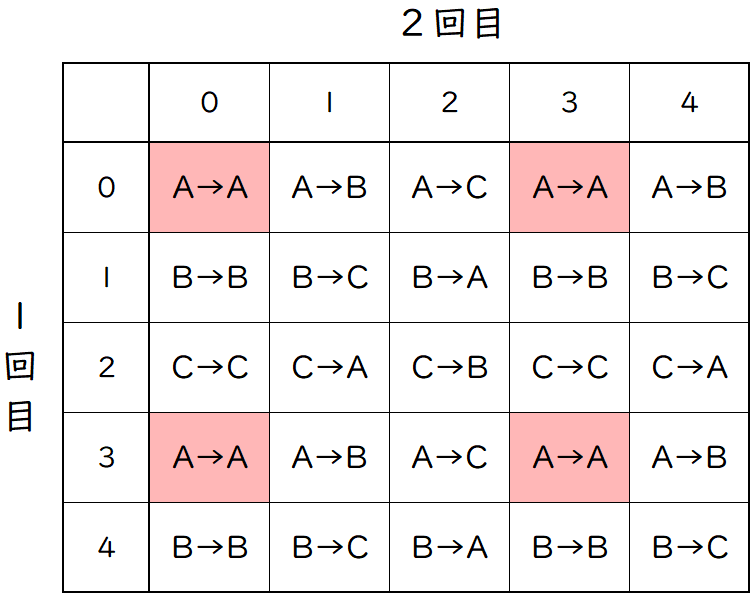
すべての場合の数は,$(\,5\times 5=\,)\;25$ 通りです。
表から,$1$ 回目も $2$ 回目も P が 頂点 A にあるのは $4$ 通りあります。
よって,求める確率は
$\dfrac{4}{\;25\;}$
です。
(3)$2$ 回目の操作後に P が頂点 A にある確率を求めなさい。
解答・解説
ー
解答$\dfrac{8}{\;25\;}$
操作を $2$ 回行ったときの,P の動き方を表にします。
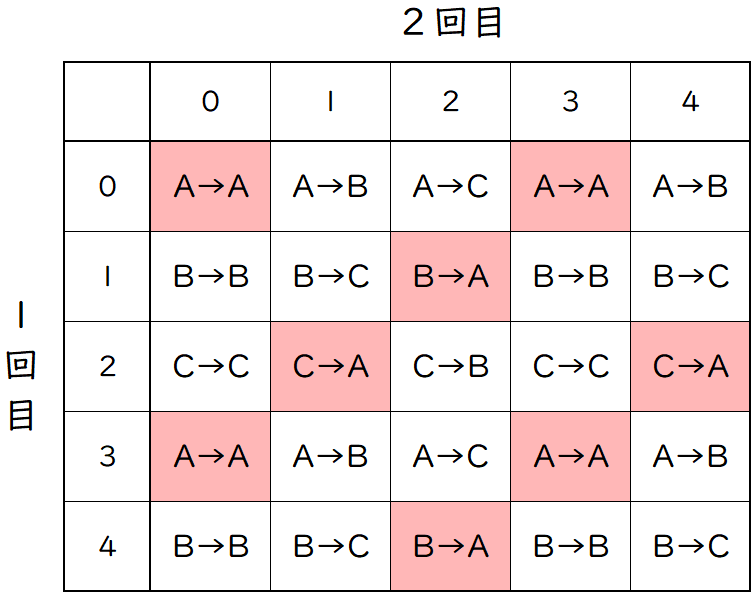
すべての場合の数は,$(\,5\times 5=\,)\;25$ 通りです。
表から,$2$ 回目の操作後に P が 頂点 A にあるのは $8$ 通りあります。
よって,求める確率は
$\dfrac{8}{\;25\;}$
です。
4下の図 1 のように,P 駅があり,P 駅から東に向かうまっすぐな線路がある。また,P 駅には車両全体の長さが $160\;\rm m$ の電車が停車しており,図 2 のように,電車の先頭部分は地点 A にある。電車は P 駅を出発してから $20$ 秒間は次第に速さを増していき,その後は P 駅を出発してから $40$ 秒後まで一定の速さで走行する。電車が P 駅を出発してから $x$ 秒後の地点 A から電車の先頭部分までの距離を $y\;\rm m$ とすると,$x$ と$y$ の関係は下の表のようになり,$0≦x≦20$ の範囲では $x$ と $y$ の関係は $y=ax^2$ で表されるという。
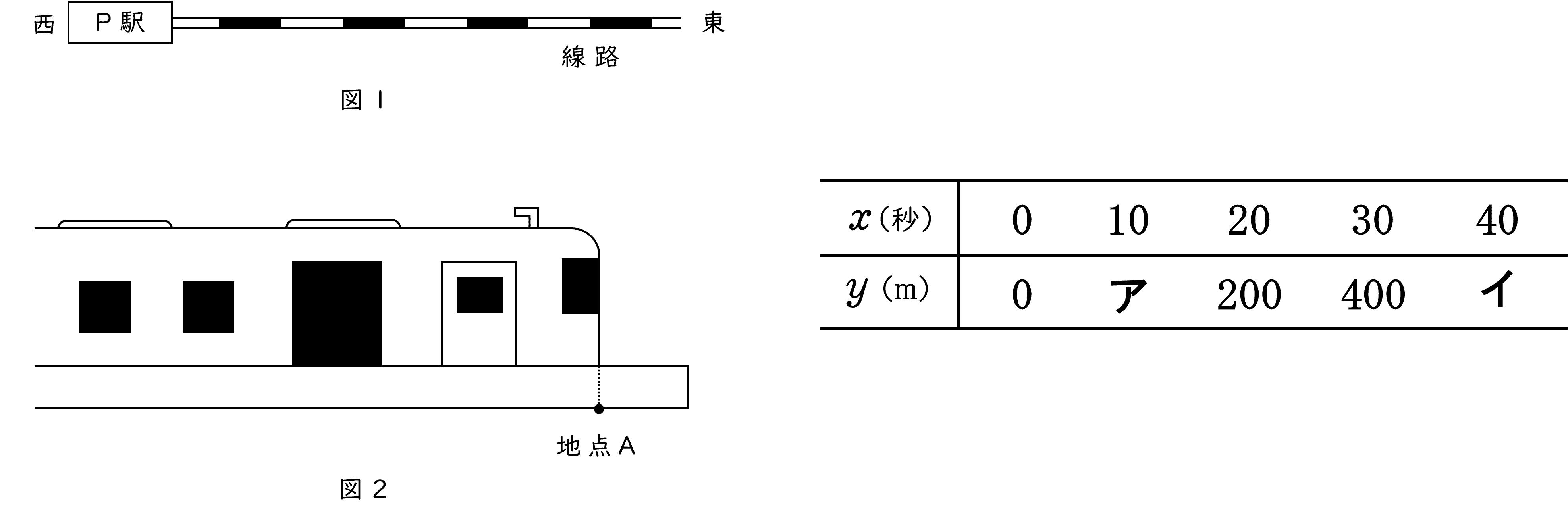
次の (1) ~ (5) の問いに答えなさい。
(1)$a$ の値を求めなさい。
解答・解説
解答$\dfrac{\,1\,}{\,2\,}$
$0≦x≦20$ の範囲では $x$ と $y$ の関係は $y=ax^2$ で表されます。
また,表から $x=20$ のとき $y=200$ です。
$y=ax^2$ に $x=20$,$y=200$ を代入すると,
$\begin{eqnarray}200&=&a \times 20^2\\[3pt]200&=&400a\\[3pt]a&=&\dfrac{1}{\;2\;}\end{eqnarray}$
(2)表中の ア,イ にあてはまる数を求めなさい。
解答・解説
解答(ア) $50\quad$(イ) $600$
(ア)$0≦x≦20$ のときを考えます。
(1) から $0≦x≦20$ の範囲では $x$ と $y$ の関係は $y=\dfrac{1}{\;2\;}x^2$ で表されます。
$y=\dfrac{1}{\;2\;}x^2$ に,$x=10$ を代入して,
$\begin{eqnarray}y&=&\dfrac{1}{\;2\;} \times 10^2\\[3pt]&=&\dfrac{1}{\;2\;} \times 100 \\[3pt] &=&50\,\rm (m)\end{eqnarray}$
(イ)$20≦x≦40$ のときを考えます。
問題文から $20≦x≦40$ の範囲では速さが一定です。表の値から速さを求めます。
$\begin{array}{c|ccc}\;\;x &\; 20 & \cdots & 30\;\, \\ \hline \;\;y & \;200 & \cdots & 400\; \ \end{array}$
速さは,$\dfrac{\;400-200\;}{\;30-20}=\dfrac{\;200\;}{10}=20 \; \rm (m/s)$
$30$ 秒から $40$ 秒の間の $10$ 秒間に進む距離は $20 \times 10 = 200\;\rm (m)$
よって,$40$ 秒のときの距離(イ)は
$30$ 秒のときの距離 $+\,200 \,\rm (m)=400+200=600\;\rm(m)$
$20≦x≦40$ の範囲では速さが一定なので, 移動距離は時間の $1$ 次関数になります。(3) で求める $1$ 次関数の式をここで求めれば,それを使って イ の値を求めることができます。
(3)$x$ の変域を $20≦x≦40$ とするとき,$y$ を $x$ の式で表しなさい。
解答・解説
解答$y=20x-200$
問題文から $20≦x≦40$ の範囲では速さが一定なので, 移動距離は時間の $1$ 次関数になります。
よって,$x$ と $y$ の関係は $y=ax+b$ で表されます。
$\begin{array}{c|ccc}\;\;x &\; 20 & \cdots & 30\;\, \\ \hline \;\;y & \;200 & \cdots & 400\; \ \end{array}$
表から変化の割合($a$)を求めます。
$a=\dfrac{\;400-200\;}{\;30-20}=\dfrac{\;200\;}{10}=20$
よって,求める式は $y=20x+b$ となり,
さらに,この式に $x=20$,$y=200$ を代入して,
$200=20 \times 20 +b$
$\quad \, b=-200$
したがって,求める式は,
$y=20x-200$ $\;(\,20≦x≦40\,) $
(4)$x$ と $y$ の関係を表すグラフをかきなさい。$(\,0≦x≦40\,)$
解答・解説
解答
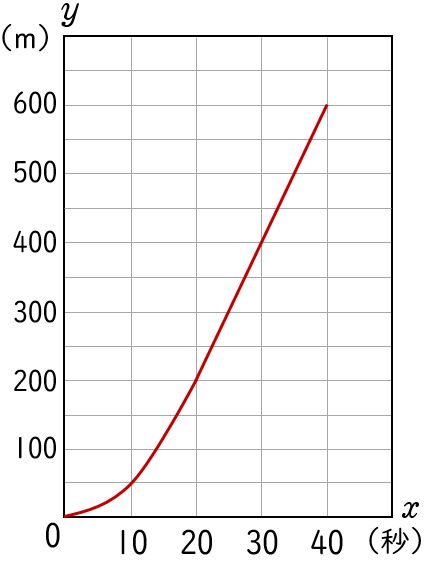
$0≦x≦20$ では,放物線 $y=\dfrac{1}{\;2\;}x^2$
$20≦x≦40$ では,直線 $y=20x-200$
(5)線路と平行な道路がある。太郎さんは,はじめ,道路上で,電車の先頭部分と並ぶ位置にいた。電車が P 駅を出発すると同時に太郎さんも走り始め,この道路を東に向かって一定の速さで走った。太郎さんは,走り始めた直後は電車より前方を走っていたが,走り始めてから $10$ 秒後に電車の先頭部分に追いつかれた。その後,太郎さんの横を電車が通り過ぎていき,やがて太郎さんは電車に完全に追い越された。太郎さんが電車に完全に追い越されたのは,電車が P 駅を出発してから何秒後であったかを求めなさい。
解答・解説
解答$24$ 秒後
太郎さんは電車と同時に走り始め,$10$ 秒後に電車の先頭に追い付かれました。
(2) で求めた通り,電車は $10$ 秒間で $50\;\rm m$ 進みます。
つまり,太郎さんは $10$ 秒間に $50\;\rm m$ 進む速さで走っていたことになります。
よって,太郎さんの走る速さは
$50 \div 10 =5$ ⇒ 秒速 $5\;\rm m$
です。
太郎さんが P 駅を出発してから $x$ 秒間に進んだ距離を $y\;\rm m$ とすると,$y$ は $x$ に比例し,$x$ と$y$ の関係は
$y=5x$
と表せます。
太郎さんの走る様子 $(\,y=5x\,)$ もグラフに書き込むと下のようになります。
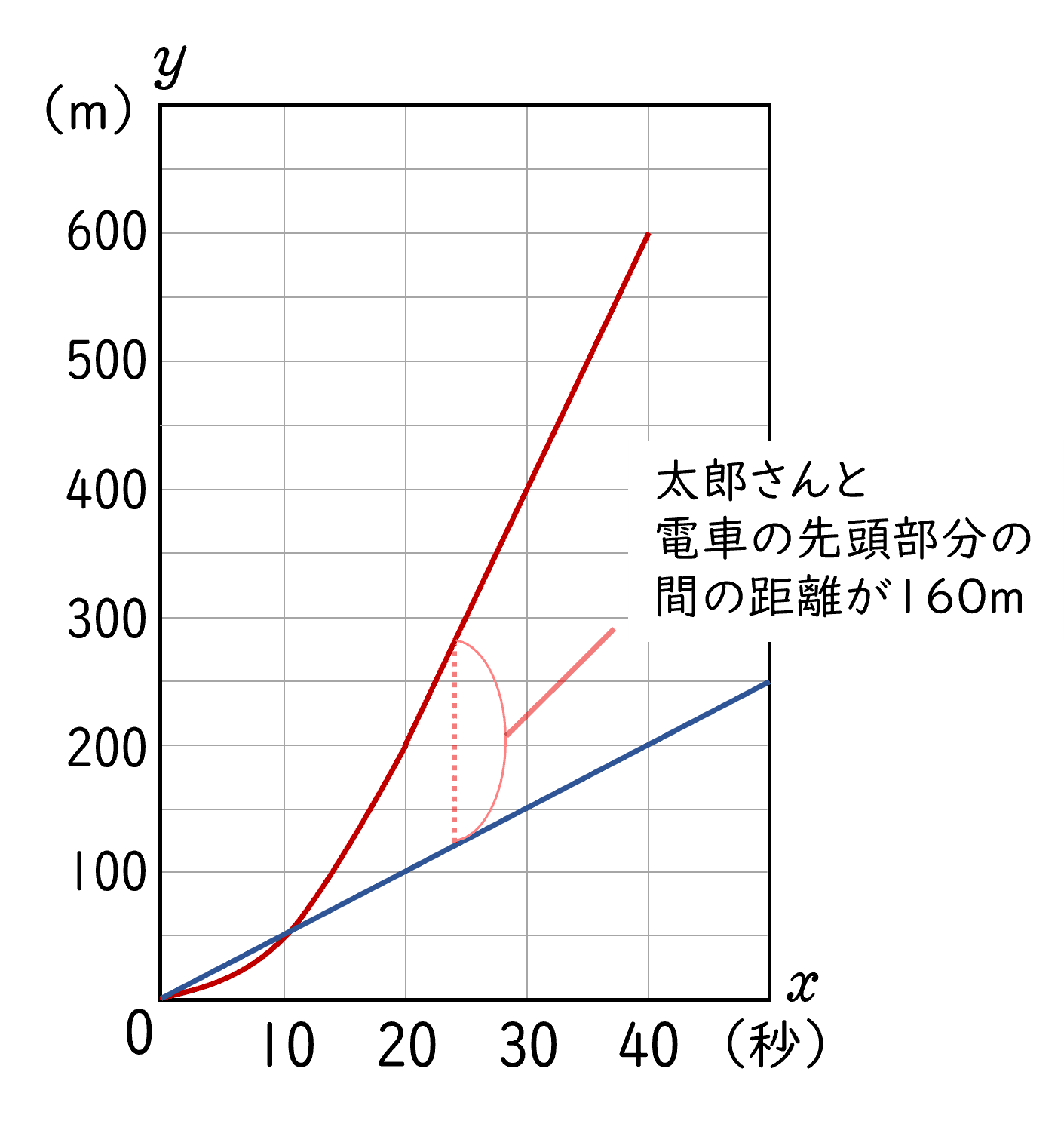
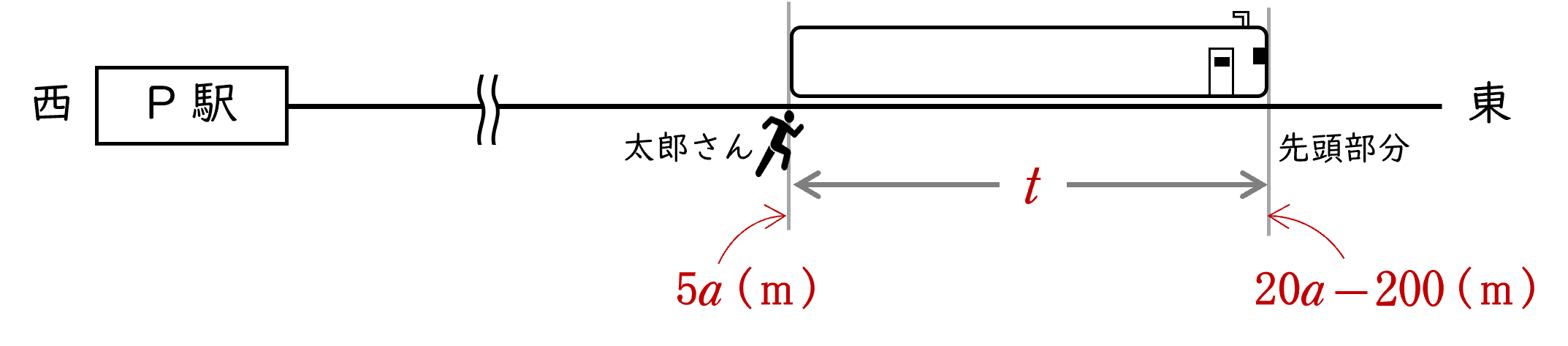
太郎さんが電車に完全に追い越されたのは,
太郎さんと電車の先頭部分の間の距離が車両の長さ $(\,160 \rm \;m\,)$ と同じになったとき
です(下の図)。

$a$ 秒後の「太郎さんと電車の先頭部分の間の距離」を $t\;\rm m$ とします。
上のグラフから,$20$ 秒後までに $t=160$ になることはないので,$20≦a≦40$ の場合を考えます。
・電車について,$\quad \;\; x=a\;$ のとき $\;y=20a-200$
・太郎さんについて,$x=a\;$ のとき $\;y=5a$
よって,$x=a\;$ のとき,
$\begin{eqnarray}t&=&(\,20a-200\,)-5a\\[3pt]&=&15a-200 \end{eqnarray}$
$t=160\;$ のとき,
$\begin{eqnarray}160&=&15a-200\\[3pt]15a&=&360\\[3pt]a&=&24 \end{eqnarray}$
したがって,太郎さんが電車に完全に追い越されたのは,電車が P 駅を出発してから $24$ 秒後です。
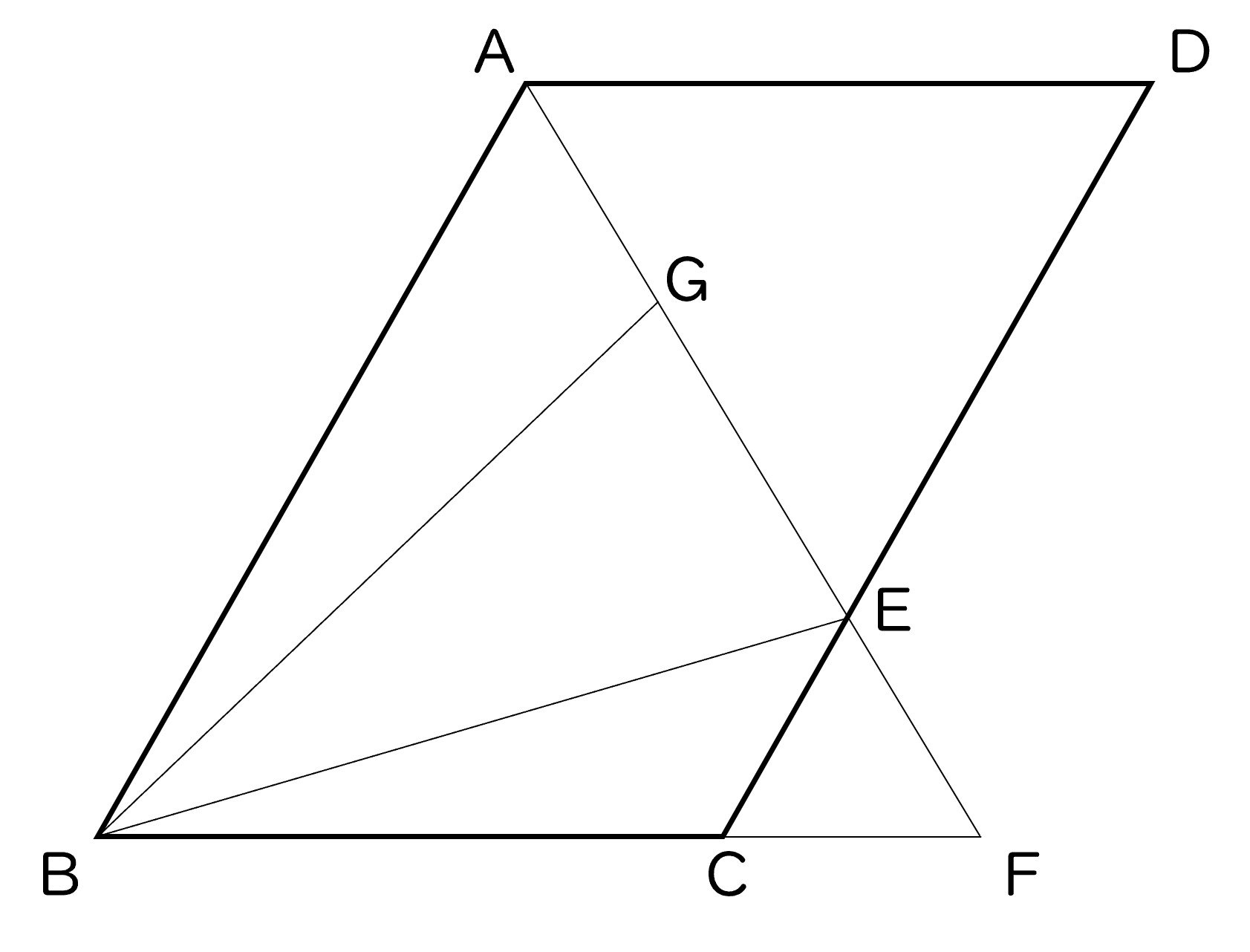
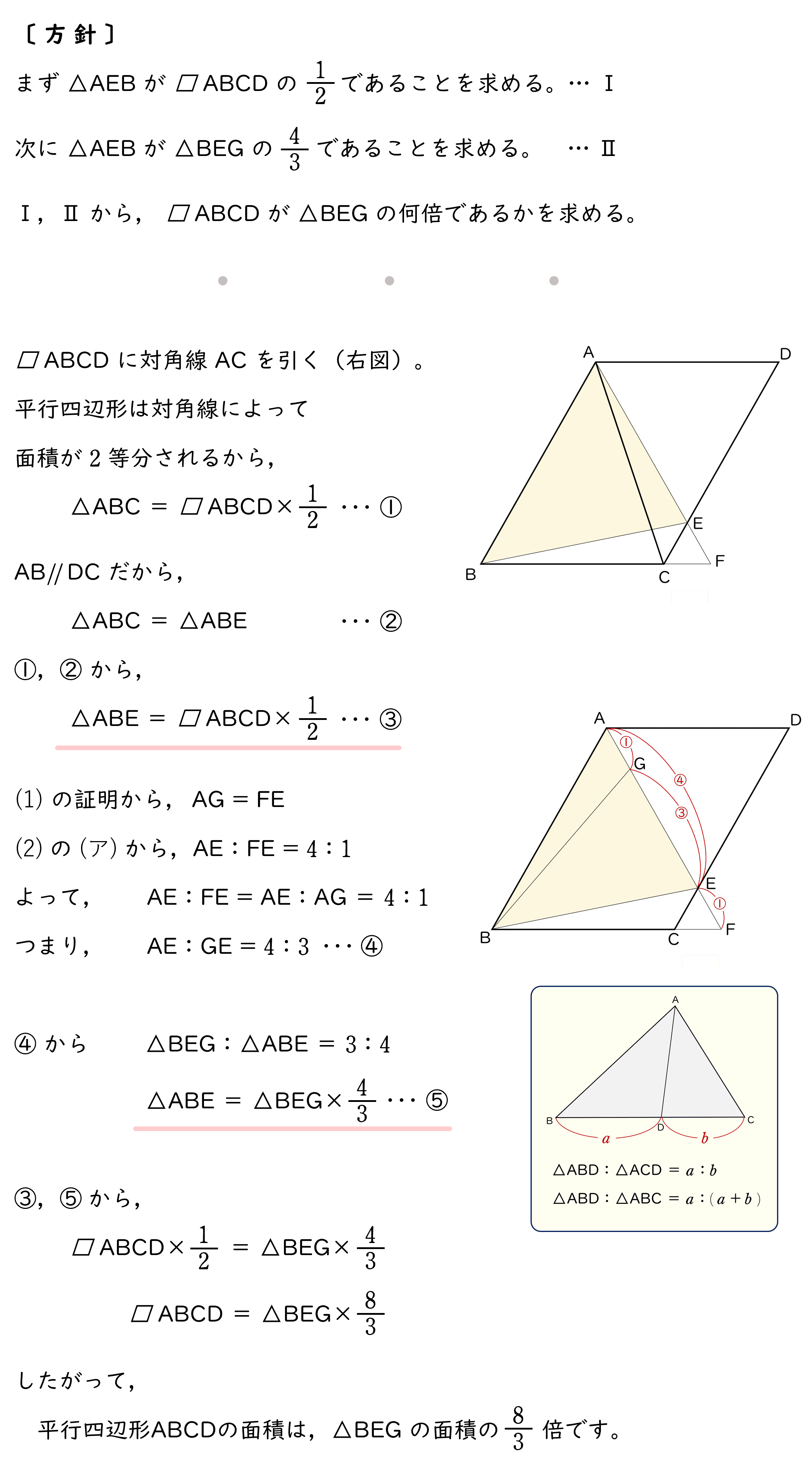
5下の図で, 四角形 ABCD は平行四辺形であり,∠BAD の二等分線と辺 CD,辺 BC を延長した直線との交点をそれぞれ E,F とする。また,点 G は線分 AF 上の点で,∠ABG=∠CBE である。
次の (1),(2) の問いに答えなさい。
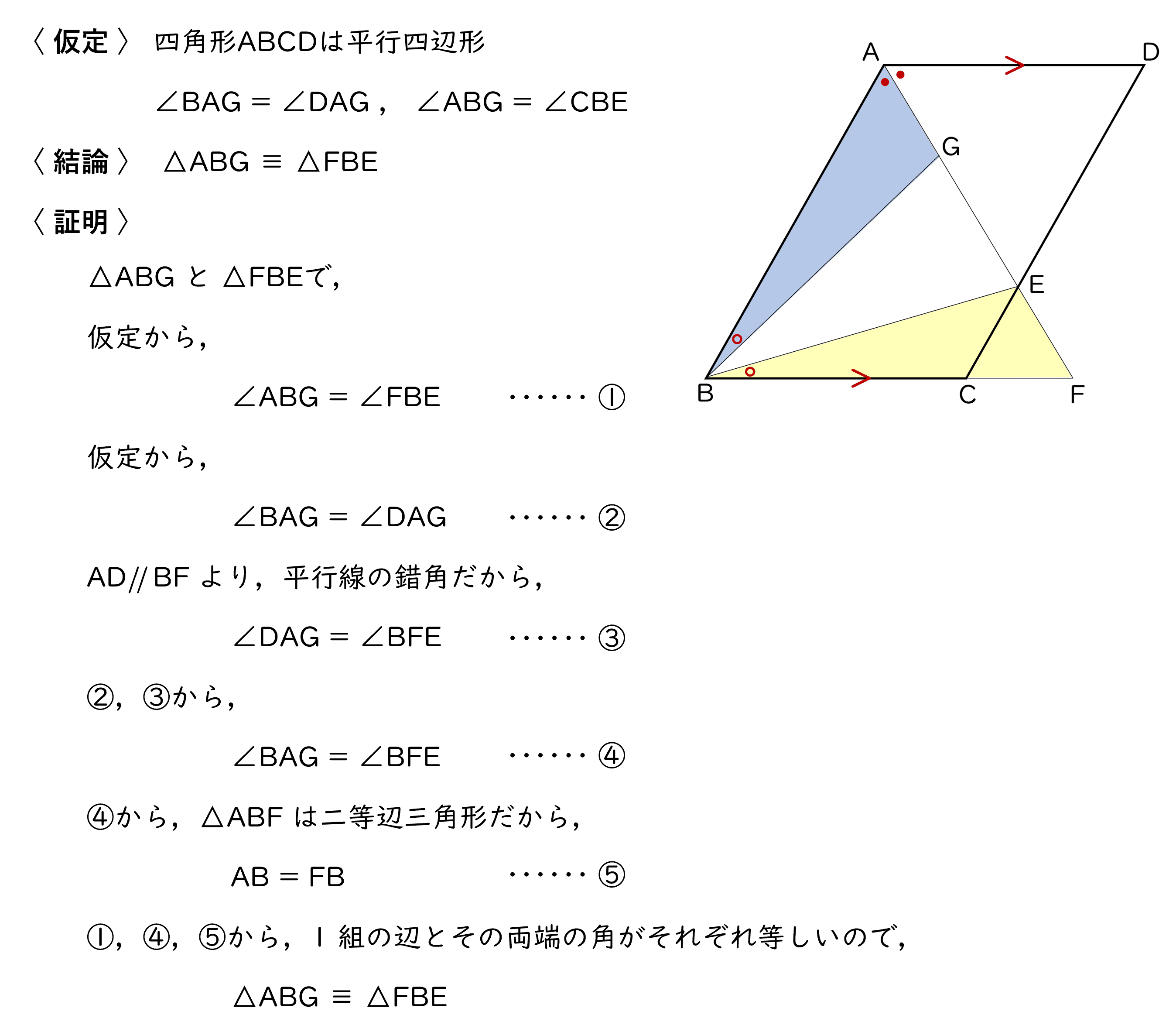
(1)△ ABG ≡ △ FBE であることを証明しなさい。
解答
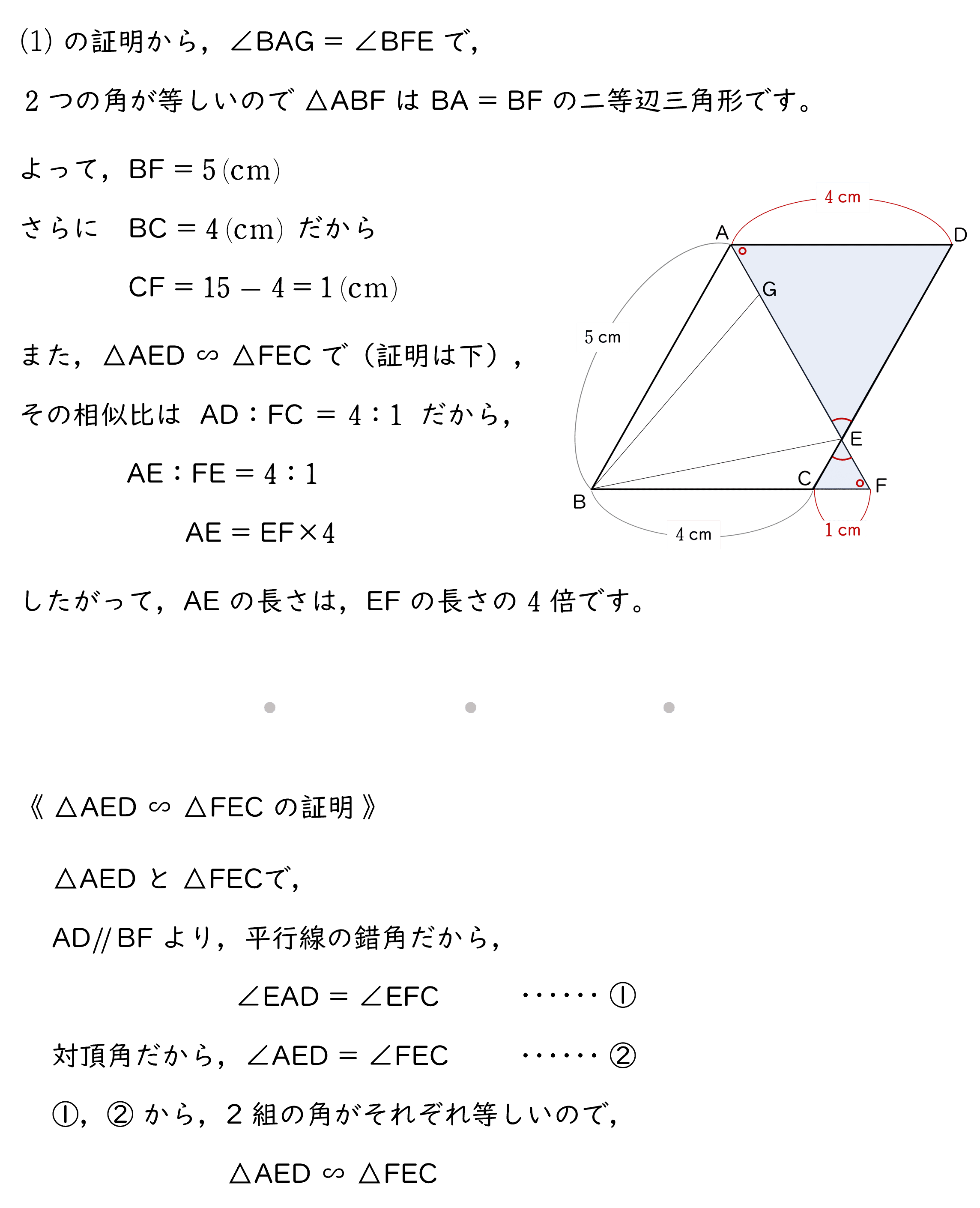
(2)AB $=5\;\rm cm$,BC $=4\;\rm cm$ のとき,
(ア)AE の長さは,EF の長さの何倍であるかを求めなさい。
解答・解説
解答$4\;$倍
(イ)平行四辺形 ABCD の面積は,△ BEG の面積の何倍であるかを求めなさい。
解答・解説
解答$\dfrac{\;8\;}{\;3\;}$ 倍
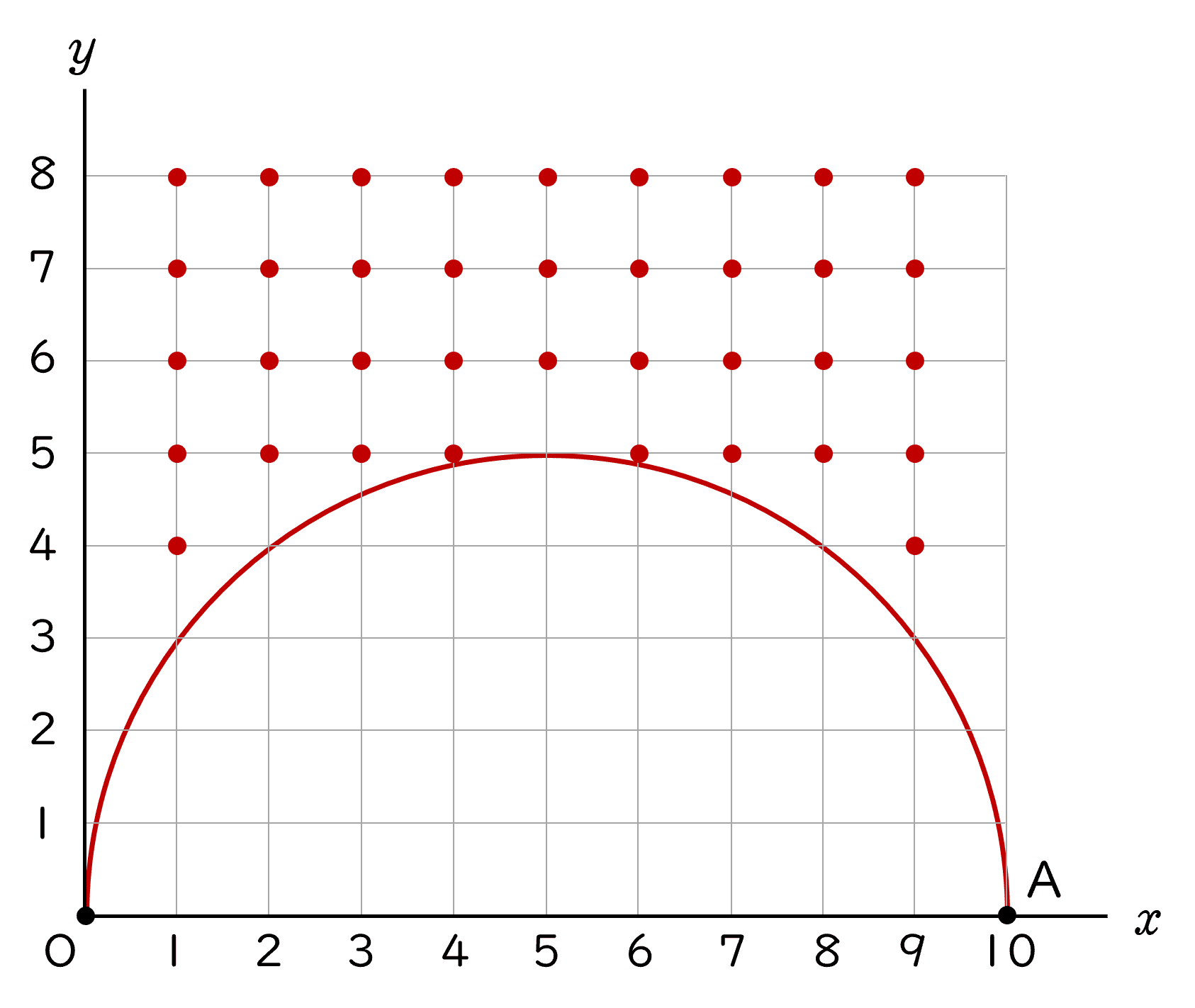
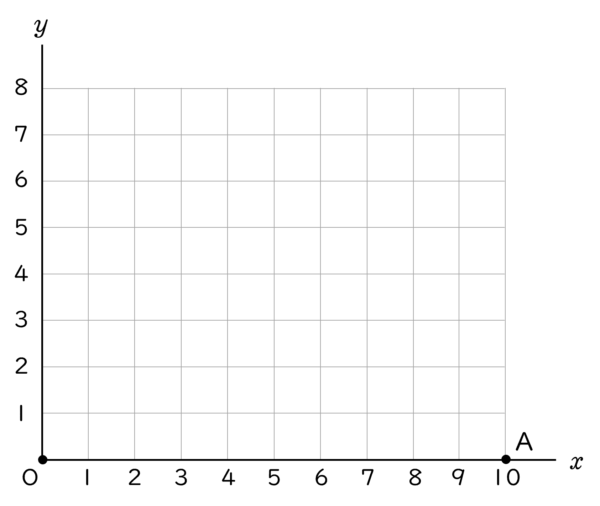
6下の図のように,平面上に座標軸,原点 O,点 A $(\,10,\;\;0\,)$ がある。この平面上に,$x$ 座標が $1$ 以上 $10$ 以下の整数で。$y$ 座標が $1$ 以上 $8$ 以下の整数である点 P をとり,O と A,A と P,P と O をそれぞれ結び,△ OAP をつくる。
次の (1) ~ (3) の問いに答えなさい。
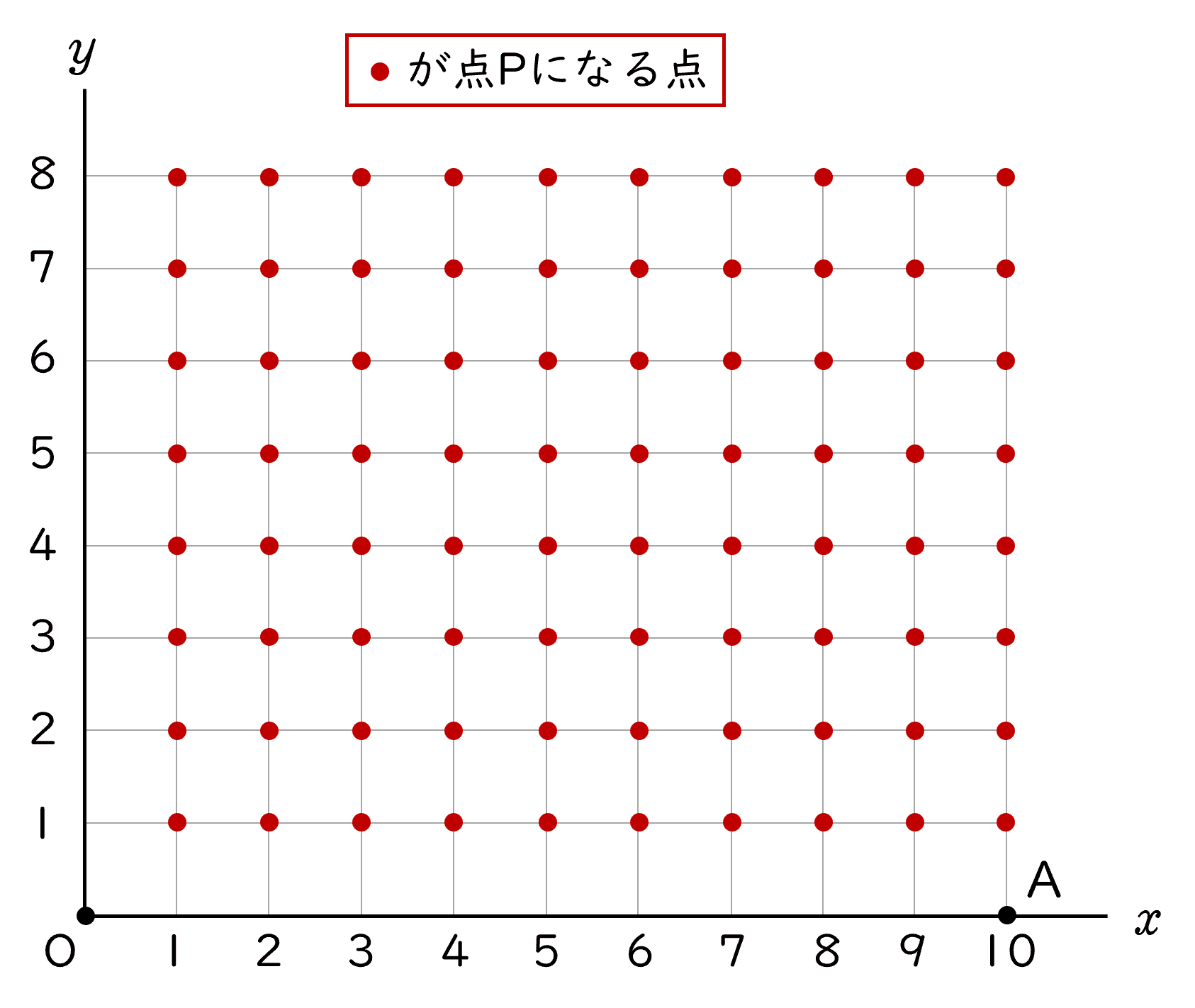
(1)P のとり方は,全部で何通りあるかを求めなさい。
解答・解説
解答$80\;$通り

(2)次の文章は,△ OAP が直角三角形となる P のとり方について,花子さんが考えたことをまとめたものである。ア ~ エ にそれぞれ当てはまる数を書きなさい。
△ OAP の内角のうち,直角となるものに着目して,次の $3$ つの場合に分けて考える。
① ∠ OAP$=90°$ となる P のとり方は,全部で ア 通りある。
② ∠ AOP$=90°$ となる P のとり方は,ない。
③ ∠ OPA$=90°$ となる P のとり方は,点 $(\,5,\;\;$ イ $\,)$,点 $(\,1,\;\;$ ウ $\,)$ など,全部で エ 通りある。
解答・解説
解答ア$\;\;8$,$\quad$イ$\;\;5$,$\quad$ウ$\;\;3$,$\quad$エ$\;\;5$

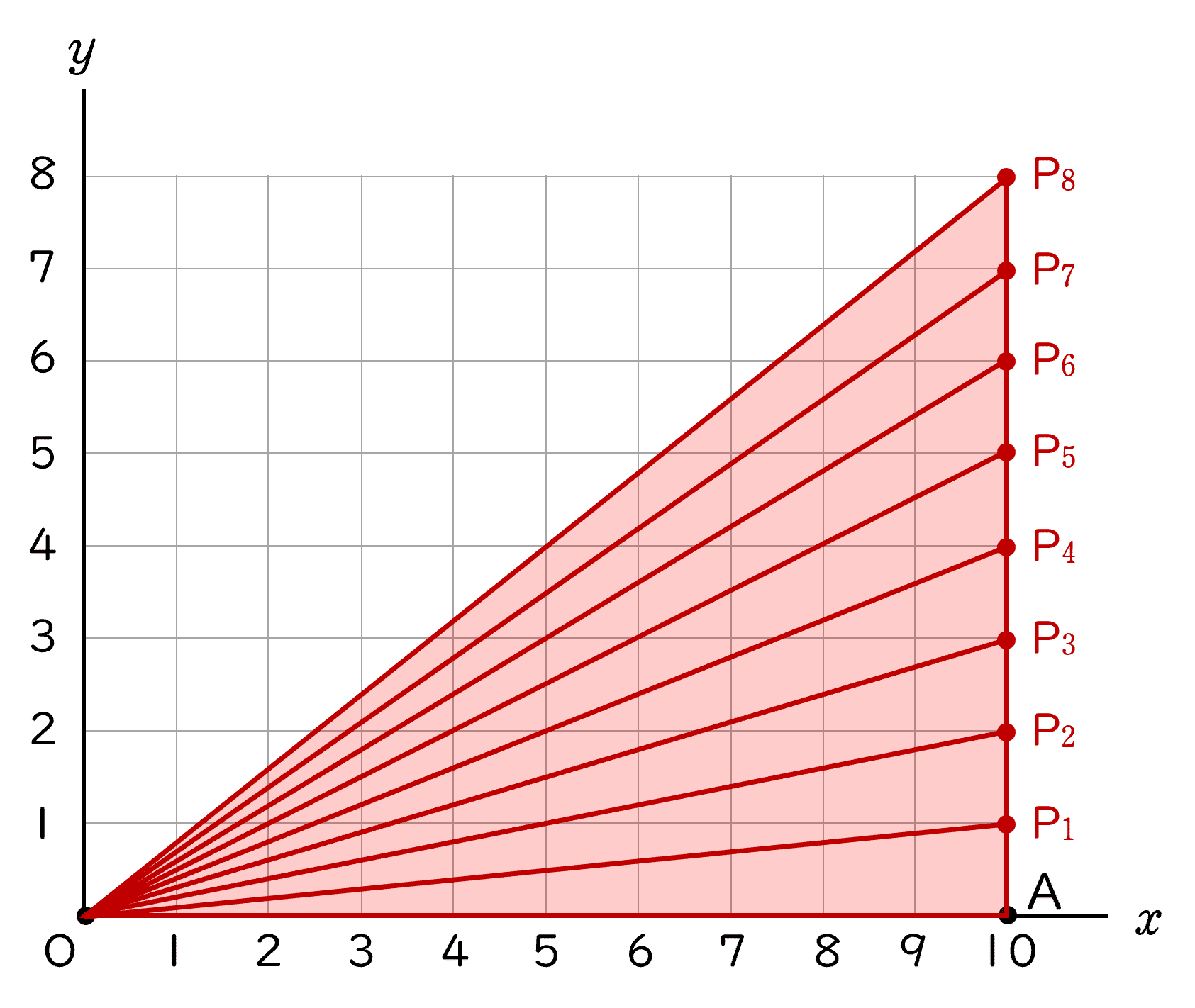

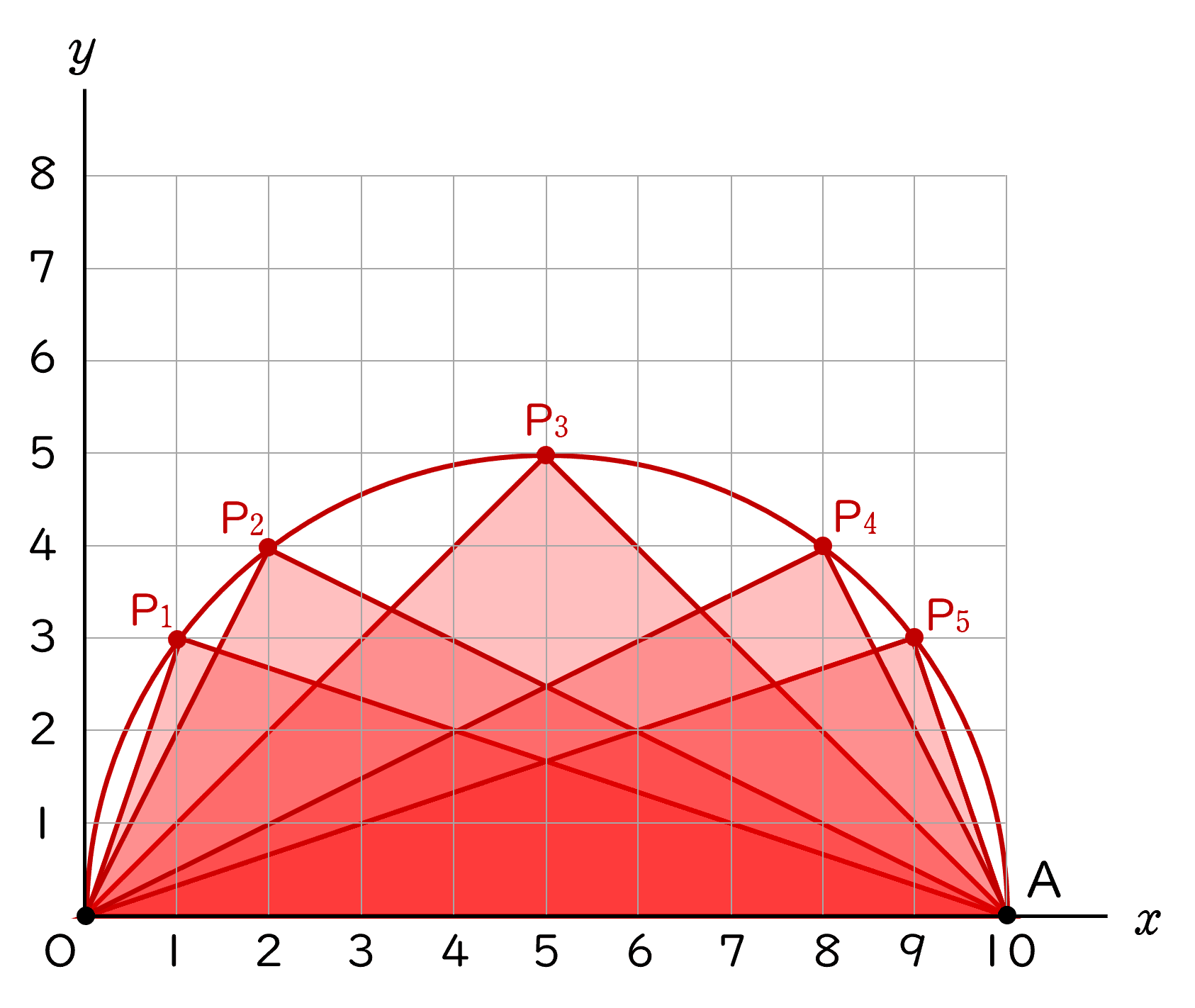
(3)△ OAP の内角が全て鋭角となる P のとり方は,全部で何通りあるかを求めなさい。
解答・解説
解答$37\;$通り