岐阜県・公立高校入試 2020年度( 令和2年度 )解答・解説編
岐阜県立高校・入学試験学力検査・数学・2020年度
1次の(1)~(6)の問いに答えなさい。
(1)$9-6\div3\;\;$を計算しなさい。
解答・解説
解答$7$
$9\color{red}-6\div 3$割り算から計算します
$=9-2$
$=7$
(2)$4x+2y=6\;\;$を $y$ について解きなさい。
解答・解説
解答$y=-2x+3$
$4x+2y=6$左辺の $4x$ を右辺に移項します
$2y=-4x+6$両辺を $2$ で割ります
$y=-2x+3$
(3)$\sqrt{\,27\,}+\sqrt{\,3\,}-\sqrt{\,12\,}\;\;$を計算しなさい。
解答・解説
解答$2\sqrt{\,3\,}$
$\sqrt{\,27\,}+\sqrt{\,3\,}-\sqrt{\,12\,}$
$=\color{red} 3\sqrt{\,3\,}+\sqrt{\,3\,}\color{black}-2\sqrt{\,3\,}$
$=4\sqrt{\,3\,}-2\sqrt{\,3\,}$
$=2\sqrt{\,3\,}$
(4)関数 $y=2x^{2}$ で,$x$ の値が $2$ から $5$ まで増加するときの変化の割合を求めなさい。
解答・解説
解答$14$
$x$ の値が $2$ から $5$ まで増加するときの変化の様子を表に表します。
$\begin{array}{c|ccc}\;\;x &\; 2 & \cdots & 5\;\, \\ \hline \;\;y & \;8 & \cdots & 50\; \ \end{array}$
変化の割合 $=\dfrac{\;y\,\sfの増加量\;}{x\,\sfの増加量}$
$=\dfrac{\;50-8\;}{\;5-2}$
$=\dfrac{\;42\;}{3}$
$=14$
(5)$1$ から $5$ までの数字を $1$ つずつ書いた $5$ 枚のカード $\boxed{1}\,\boxed{2}\,\boxed{3}\,\boxed{4}\,\boxed{5}$ が,袋の中に入っている。この袋の中からカードを $1$ 枚取り出して,そのカードの数字を十の位の数とし,残った $4$ 枚のカードから $1$ 枚取り出して,そのカードの数字を一の位の数として,$2$ けたの整数をつくる。このとき,つくった整数が偶数になる確率を求めなさい。
解答・解説
解答$\dfrac{2}{\;5\;}$
取り出し方のすべての場合を樹形図(下の図)で表します。
全ての場合の数は,$4\times 5=20$ (通り)です。
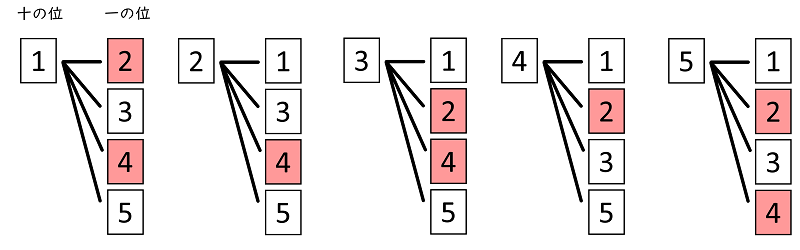
つくった整数が偶数になる場合は,図から,
$12$,$14$,$24$,$32$,$34$,$42$,$52$,$54$ の $8$ 通りです。
その確率は,
$\dfrac{8}{\;20\;}=\dfrac{2}{\;5\;}$
(6)下の図は,線分 AB を $2$ つの線分に分け,それぞれの線分を直径として作った円である。太線は $2$ つの半円の弧をつなげたものである。AB $=10$ cm のとき,太線の長さを求めなさい。(円周率は $\pi$ を用いなさい。)
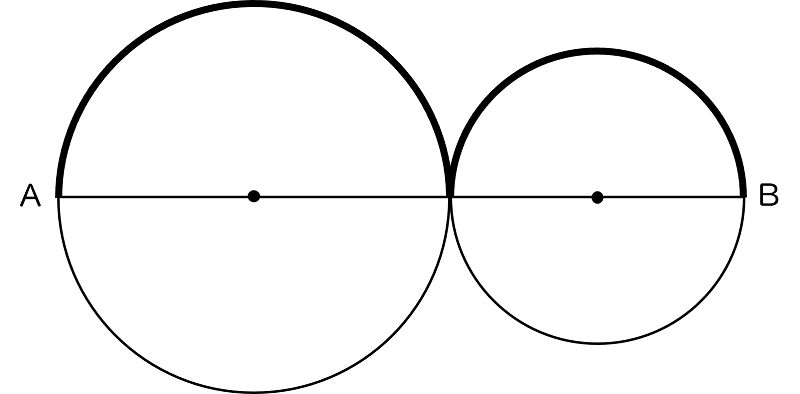
解答・解説
解答$5\pi$ cm
下の図のように,2 つの円の接点を 点 C とし,
また,AC $=a$ cm とする。
このとき,BC $=(10-a)$ cm になります。
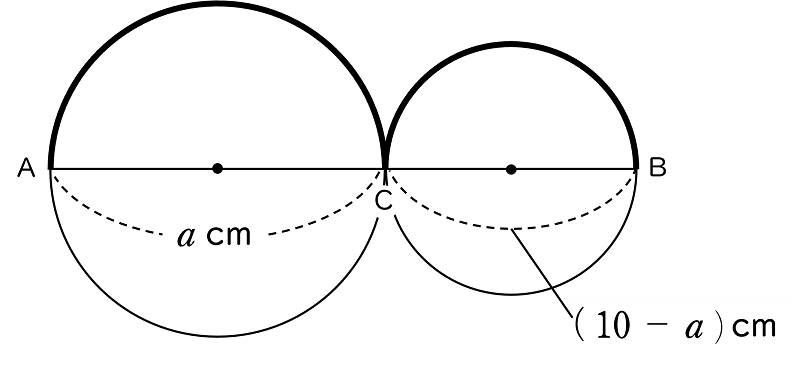
$\stackrel{\Large\frown}{\small\sf AC}\;=a \times \pi \times \dfrac{1}{\;2\;}$
$=\dfrac{1}{\;2\;}\pi a$ (cm)
$\stackrel{\Large\frown}{\small\sf BC}\;=(10-a) \times \pi \times \dfrac{1}{\;2\;}$
$=\dfrac{1}{\;2\;}\pi(10-a)$ (cm)
よって,
$\stackrel{\Large\frown}{\small\sf AC}+\stackrel{\Large\frown}{\small\sf BC}\;=\dfrac{1}{\;2\;}\pi a + \dfrac{1}{\;2\;}\pi(10-a)$
$=\dfrac{1}{\;2\;}\pi a + 5\pi - \dfrac{1}{\;2\;}\pi a$
$=5\pi$ (cm)
2右の表は,A 中学校の生徒 $39$ 人と B 中学校の生徒 $100$ 人の通学時間を調べ,度数分布表に整理したものである。
次の (1) ~ (3) の問いに答えなさい。
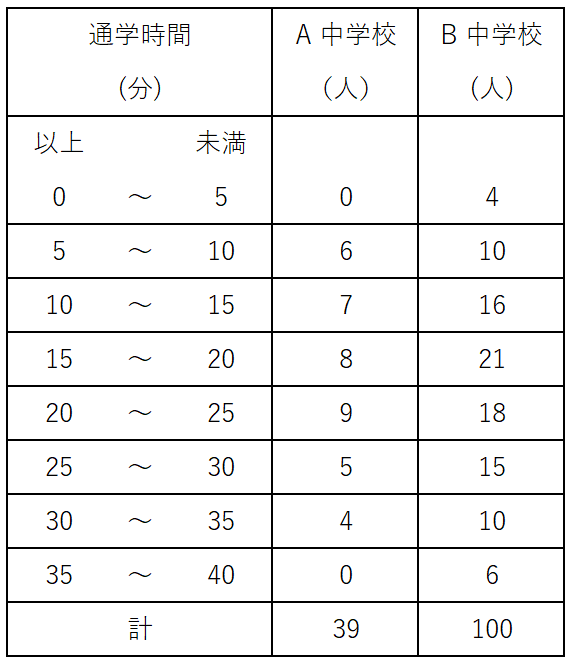
(1)A 中学校の通学時間の最頻値を求めなさい。
解答・解説
解答$22.5$ (分)
度数分布表において最頻値は,度数が一番多い階級の階級値です。
A 中学校で,度数が一番多い階級は,$20$ 分以上 $25$ 分未満の階級なので,
その階級値は,
$(\,20+25\,)\div 2 = 22.5$ (分)
これが A 中学校の最頻値です。
(2)B 中学校の通学時間が $15$ 分未満の生徒の相対度数を求めなさい。
解答・解説
解答$0.3$
度数分布表から,B 中学校の通学時間が $15$ 分未満の生徒の数は,
$4+10+16=30$ (人)
よって,その相対度数は,
$\dfrac{30}{\;100\;}=0.3$
(3)右の度数分布表について述べた文として正しいものを,次の ア~エ の中からすべて選び,符号で書きなさい。
アA 中学校と B 中学校の,通学時間の最頻値は同じである。
イA 中学校と B 中学校の,通学時間の中央値は同じ階級にある。
ウA 中学校より B 中学校の方が,通学時間が $15$ 分未満の生徒の相対度数が大きい。
エA 中学校より B 中学校の方が,通学時間の範囲が大きい。
解答・解説
解答イ,エ
ア について
度数分布表において最頻値は,度数が一番多い階級の階級値です。
(1)から,A 中学校で,度数が一番多い階級は,$20$ 分以上 $25$ 分未満の階級です。
また, B 中学校で,度数が一番多い階級は,$15$ 分以上 $20$ 分未満の階級です。
度数が一番多い階級が異なるので,最頻値も異なります。
よって,正しくありません。
イ について
中央値は,データを大きさの順に並べたときの,真ん中にある値です。
A 中学校の度数の合計は $39$ 人なので,
中央値は通学時間が短い順に並べたときの $20$ 番目の値です。
この値がある階級は $15$ 分以上 $20$ 分未満の階級です。
また,B 中学校の度数の合計は $100$ 人なので,
中央値は通学時間が短い順に並べたときの $50$ 番目と $51$ 番目の平均の値です。
この値がある階級は $15$ 分以上 $20$ 分未満の階級です。
よって,A 中学校と B 中学校の,通学時間の中央値は同じ階級にあります。
ウ について
(2) から,B 中学校の通学時間が $15$ 分未満の生徒の相対度数は $0.3$ です。
また,度数分布表から,A 中学校の通学時間が $15$ 分未満の生徒の数は,
$0+6+7=13$ (人)
その相対度数は,
$\dfrac{13}{\;39\;}=0.333・・・$
よって,A 中学校の相対度数の方が大きいので,正しくありません。
エ について
範囲は,データの最大値と最小値との差です。
A 中学校の通学時間の最小値は,
$5$ 分以上 $10$ 分未満の階級の値で,
最大値は,
$30$ 分以上 $35$ 分未満の階級の値です。
また,B 中学校の通学時間の最小値は,
$0$ 分以上 $5$ 分未満の階級の値で,
最大値は,
$35$ 分以上 $40$ 分未満の階級の値です。
これらより,
最小値がより小さい値であるのは B 中学校であり,
最大値がより大きい値であるのも B 中学校であることが分かります。
よって,A 中学校より B 中学校の方が,通学時間の範囲が大きいといえます。
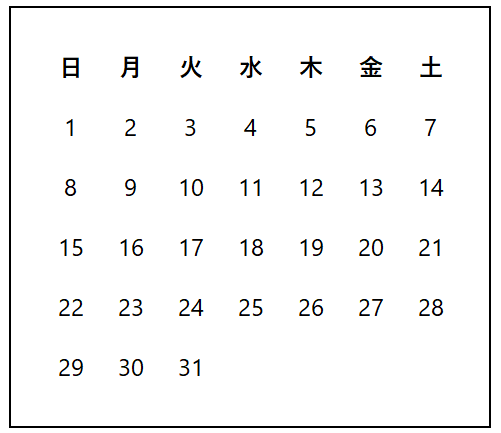
3右のカレンダーの中にある $3$ つの日付の数で,次の ①~③ の関係が成り立つものを求める。
①最も小さい数と $2$ 番目に小さい数の $2$ つの数は,上下に隣接している。
②$2$ 番目に小さい数と最も大きい数の $2$ つの数は,左右に隣接している。
③最も小さい数の $2$ 乗と$2$ 番目に小さい数の $2$ 乗との和が,最も大きい数の $2$ 乗に等しい。
次の (1),(2) の問いに答えなさい。
(1)$2$ 番目に小さい数を $x$ とすると,
(ア)①から,最も小さい数を $x$ を使った式で表しなさい。
解答・解説
解答$x-7$
上下に隣接している数について,
上の数は下の数より $7$ 小さい数になっています。
つまり,最も小さい数は,$2$ 番目に小さい数よりも $7$ 小さい数です。
よって,最も小さい数は,$x-7$ と表せます。
(イ)②から,最も大きい数を $x$ を使った式で表しなさい。
解答・解説
解答$x+1$
左右に隣接している数について,
右の数は左の数より $1$ 大きい数になっています。
つまり,最も大きい数は,$2$ 番目に小さい数よりも $1$ 大きい数です。
よって,最も大きい数は,$x+1$ と表せます。
(ウ)①,②,③から,$x$ についての 2 次方程式をつくり,$x^{2}+ax+b=0$ の形で表しなさい。
解答・解説
解答$x^{2}-16x+48=0$
③から,次の式をつくることができます。
最も小さい数の $2$ 乗 $+$ $2$ 番目に小さい数の $2$ 乗 $=$ 最も大きい数の $2$ 乗
$(\,x-7\,)^{2}+x^{2}=(\,x+1\,)^{2}$
$(\,x^{2}+-14x+49\,)+x^{2}=x^{2}+2x+1$
$x^{2}-16x+48=0$
(2)$3$ つの数を求めなさい。
解答・解説
解答$5$,$12$,$13$
(1) の (ウ) でつくった 2 次方程式を解きます。
$x^{2}-16x+48=0$
$(\,x-4\,)(\,x-12\,)=0$
$x=4$,$x=12$
〔1〕$x=4$ のとき,カレンダーではその上の数( 最も小さい数 )がありません。
よって,不適切です。
〔2〕$x=12$ のとき,カレンダーでは,
その上の数( 最も小さい数 )は $5$,
その右の数( 最も大きい数 )は $13$ です。
よって,$3$ つの数は $5$,$12$,$13$ です。
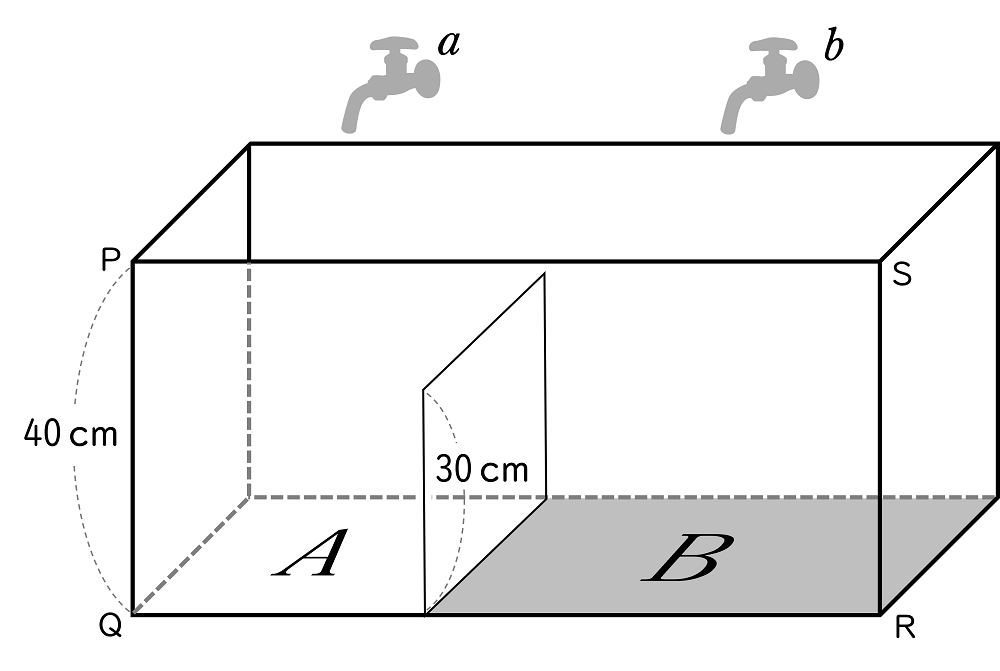
4右の図のように,水平に置かれた直方体状の容器があり,その中には水をさえぎるために,底面と垂直な長方形のしきりがある。しきりで分けられた底面のうち,頂点 Q を含む底面を $A$,頂点 R を含む底面を $B$ とし,$B$ の面積は $A$ の面積の $2$ 倍である。管 $a$ を開くと $A$ 側から水が入り,管 $b$ を開くと $B$ 側から水が入る。$a$ と $b$ の $1$ 分間あたりの給水量は同じで,一定である。
$A$ 側の水面の高さは辺 QP で測る。いま,$a$ と $b$ を同時に開くと,$10$ 分後に $A$ 側の水面の高さが $30$ cm になり,$20$ 分後に容器が満水になった。管を開いてから $x$ 分後の $A$ 側の水面の高さを $y$ cm とすると,$x$ と $y$ との関係は下の表のようになった。ただし,しきりの厚さは考えないものとする。

次の (1) ~ (4) の問いに答えなさい。
(1) ~ (3) の解説
管 $a$ と 管 $b$ の給水量は同じで,一定だから,
水面の高さは時間の経過とともに一定の割合で増加していきます。
つまり,$y$ の値が増加するすべての時間において,
$y$ は $x$ の一次関数であるといえます。
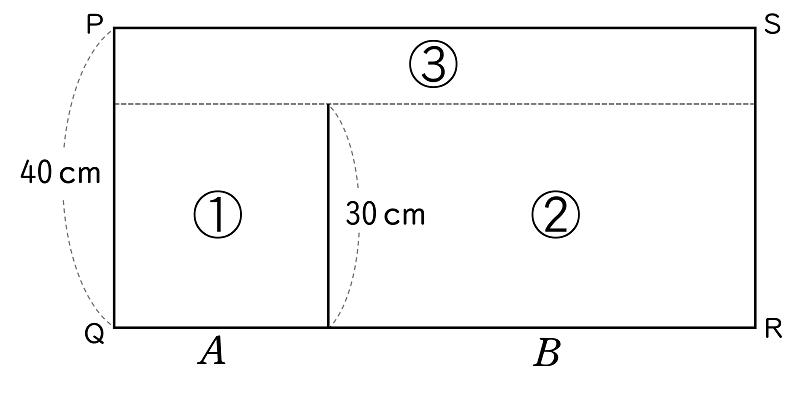
下の図( 容器を面 PQRS から見た図 )で考えます。
容器を図のように ①,②,③ の部分に分けます。
水は ① が満水になった後,② が満水になり,最後に ③ が満水になります。
底面 $B$ の面積は底面 $A$ の面積の $2$ 倍だから,
② の部分の容積は ① の部分の容積の $2$ 倍です。
$A$ の面積を $V$ cm$^{2}$ とすると,$B$ の面積は $2V$ cm$^{2}$ になり,
① の容積は,$V \times 30=30V$ (cm$^{3}$)
② の容積は,$2V \times 30=60V$ (cm$^{3}$)
③ の容積は,$(\,V+2V\,) \times (\,40-30\,)=30V$ (cm$^{3}$)
と表すことができます。
問題文から,給水を始めて $10$ 分後に ① の部分が満水になったことから,
$a$ は1分間に,$30V \div 10=3V$ (cm$^{3}$) 給水しています。
$b$ も同じです。
$x$ と $y$ との関係を考えていきます。
〔1〕給水を始めてから ① が満水になるまで
$x$ の変域は $(\,0≦x≦10\,)$ で,
$x$ と $y$ の変化の様子は次の表のようになります。
$\begin{array}{c|ccc}\;\;x &\; 0 & \cdots & 10\;\, \\ \hline \;\;y & \;0 & \cdots & 30\; \ \end{array}$
$x$ と $y$ の関係を表す式を $y=ax+b$ と表すと,
$a=\dfrac{\;30-0\;}{\;10-0}=\dfrac{\;30\;}{10}=3$
よって,求める式は $y=3x+b$ となり,
さらに,この式に $x=0$,$y=0$ を代入して,
$0=3\times 0 +b$
$b=0$
したがって,給水を始めてから ① が満水になるまでの
$x$ と $y$ の関係を表す式は $y=3x$ $\;(\,0≦x≦10\,) $
※ 実際には $y$ が $x$ に比例していることは明らかなので,
求める式を $y=ax$ とし,$x=10$,$y=30$ を代入して $a$ を求めます。
〔2〕① が満水になってから ② が満水になるまで
① が満水になると,① から溢れた水は ② に入っていきます。
その間 $y$ の値は一定で,$30$ のままです。
この状態は,② が満水になるまで続きます。
その間の時間の $x$ と $y$ の関係を表す式は,$y=30$ です。
給水を始めてから,①,② が満水になるまでの時間を求めます。
$a$ と $b$ 両方を同時に開くと,
$1$ 分間に $3V\times 2 = 6V$ (cm$^{3}$) ずつ給水されます。
また,① と ② の容積の合計は,$30V+60V=90V$(cm$^{3}$) です。
これらから,給水を始めてから,①,② が満水になるまでの時間は,
$90V\div 6V = 15$ (分)
したがって,① が満水になってから ② が満水になるまでの
$x$ と $y$ の関係を表す式は $y=3x$ $\;(\,0≦x≦10\,) $
〔3〕② が満水になってから ③ が満水になるまで
③ に水が入り始めるのは〔2〕から,給水を始めてから $15$ 分後です。
また,問題文から ③ が満水になるのは,始めから $20$ 分後です。
これらから,$x$ の変域は $(\,15≦x≦20\,)$ です。
$x$ と $y$ の変化の様子は次の表のようになります。
$\begin{array}{c|ccc}\;\;x &\; 15 & \cdots & 20\;\, \\ \hline \;\;y & \;30 & \cdots & 40\; \ \end{array}$
$x$ と $y$ の関係を表す式を $y=ax+b$ と表すと,
$a=\dfrac{\;40-30\;}{\;20-15\;}=\dfrac{\;10\;}{5}=2$
よって,求める式は $y=2x+b$ となり,
さらに,この式に $x=15$,$y=30$ を代入して,
$30=2\times 15 +b$
$\;\;b=0$
したがって, $x$ と $y$ の関係を表す式は $y=2x$ $\;(\,15≦x≦20\,) $
(1)表中の ア ,イ に当てはまる数を求めなさい。
解答・解説
解答ア $18$ イ $30$
(1) ~ (3) の解説 から,
$0≦x≦10$ のとき, $x$ と $y$ の関係を表す式は $y=3x$ だから,
$x=6$ のときの $y$ の値は,
$y=3\times 6 = 18$ア18
(1) ~ (3) の解説 から,
$10≦x≦15$ のとき, $x$ と $y$ の関係を表す式は $y=30$ だから,
$x=15$ のときの $y$ の値は $30$ です。イ30
(2)$x$ と $y$ の関係を表すグラフをかきなさい。$(\,0≦x≦20\,)$
解答・解説
解答
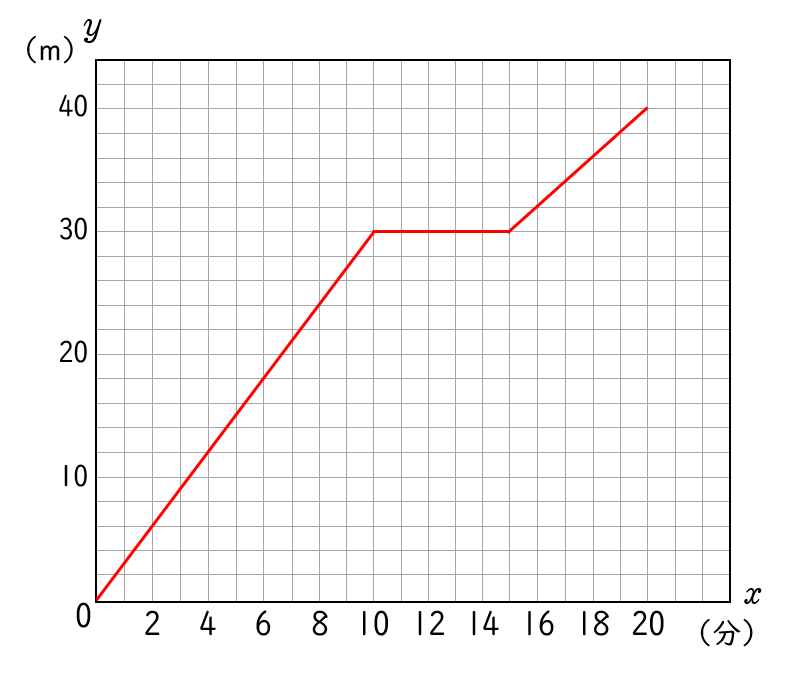
(1) ~ (3) の解説から,
$x$ と $y$ の関係は下の表のようになります。
$\begin{array}{c|ccccccc}\;\;x &\; 0 & \cdots & 10 & \cdots & 15 & \cdots & 20 \;\, \\ \hline \;\;y & \;0 & \cdots & 30 & \cdots & 30 & \cdots & 40 \; \ \end{array}$
よって,座標 $(\;0,\;0\;)$,$(\;10,\;30\;)$, $(\;15,\;30\;)$, $(\;20,\;40\;)$ を直線で結びます。
(3)$x$ の変域を次の (ア),(イ) とするとき,$x$ と $y$ との関係を式で表しなさい。
(ア)$0≦x≦10$ のとき
解答・解説
解答$y=3x$
(1) ~ (3) の解説 の通りです。
(イ)$15≦x≦20$ のとき
解答・解説
解答$y=2x$
(1) ~ (3) の解説 の通りです。
(4)$B$ 面の水面の高さは辺 RS で測る。管を開いてから容器が満水になるまでの間で,$A$ 側の水面の高さと $B$ 側の水面の高さの差が $2$ cm になるときが $2$ 回あった。管を開いてから何分何秒後であったかを,それぞれ求めなさい。
解答・解説
解答$1$ 分 $20$ 秒後,$14$ 分 $20$ 秒後
管 $a$ と 管 $b$ の給水量は同じで,
底面 $B$ の面積は底面 $A$ の面積の $2$ 倍だから,
① が満水になったとき ( 給水を開始して $10$ 秒後 ),
② には ① の半分の高さまで水が入っています。
つまり,
$A$ 側の水面の高さが $30$ cm になったとき,
$B$ 側の水面の高さは $15$ cm になっています。
まず,① が満水になるまでの間 $(\,0≦x≦10\,)$,
$A$ 側の水面は $1$ 分間に $30\div 10=3$ (cm) ずつ増加し,
$B$ 側の水面は $1$ 分間に $15\div 10=1.5$ (cm) ずつ増加します。
よって,$A$ 側と $B$ 側の水面の高さの差は,
$1$ 分間に $3-1.5=1.5$ (cm) ずつ増加していきます。… ア
次に,① が満水になってから,② が満水になるまでの間は,
$A$ 側の水面の高さは $30$ cm のままで,
$B$ 側の水面の高さだけが上昇していきます。
その時,② には $a$ と $b$ 両方から給水されることになるので,
$B$ 側の水面は,$b$ だけで給水するときの $2$ 倍,
つまり,$1$ 分間に $1.5\times 2 =3$ (cm) ずつ増加します。
よって,$A$側 の水面と$B$ 側の水面の高さの差は,
$1$ 分間に $3$ cm ずつ縮まっていきます。… イ
これらのことから,
$A$ 側の水面の高さと $B$ 側の水面の高さの差が $2$ cm になるときは,
〔1〕給水を始めてから $a$ が ① を,$b$ が ② に給水している間
と,
〔2〕① が満水になってから,② が満水になるまでの間
のそれぞれに $1$ 回ずつあることが分かります。
〔1〕給水を始めてから $a$ が ① を,$b$ が ② に給水している間
はじめ水面の高さの差は $0$ cm です。
上の ア から,水面の高さの差は,
$1$ 分間に $1.5$ (cm) ずつ増加していくので,
差が $2$ cm になるまでの時間は,
$2\div 1.5 = 2\div\dfrac{3}{\;2\;}$
$=2\times \dfrac{2}{\;3\;}$
$=\dfrac{4}{\;3\;}$
$=1\dfrac{1}{\;3\;}$ (分)
$=1$ 分 $20$ 秒
〔2〕① が満水になってから,② が満水になるまでの間
① が満水になったとき,
$A$ 側の水面の高さは $30$ cm で,
$B$ 側の水面の高さは $15$ cm なので,
その差は $30-15=15$ (cm) です。
上の イ から,この差は $1$ 分間に $3$ cm ずつ縮まっていくので,
差が $2$ cm になるには,$15-2=13$ (cm) 縮まればよいです。
それまでの時間は,
$13\div 3 = \dfrac{\;13\;}{3}$
$=4\dfrac{1}{\;3\;}$ (分)
$=4$ 分 $20$ 秒
給水を開始してからの時間は,
$10$ 分 $+$ $4$ 分 $20$ 秒 $=$ $14$ 分 $20$ 秒
別 解
管を開いてから $x$ 分後の $B$ 側の水面の高さを $y$ cm としたときの
$x$ と $y$ との関係を表すグラフ $(\,0≦x≦15\,)$ を青線で表します。
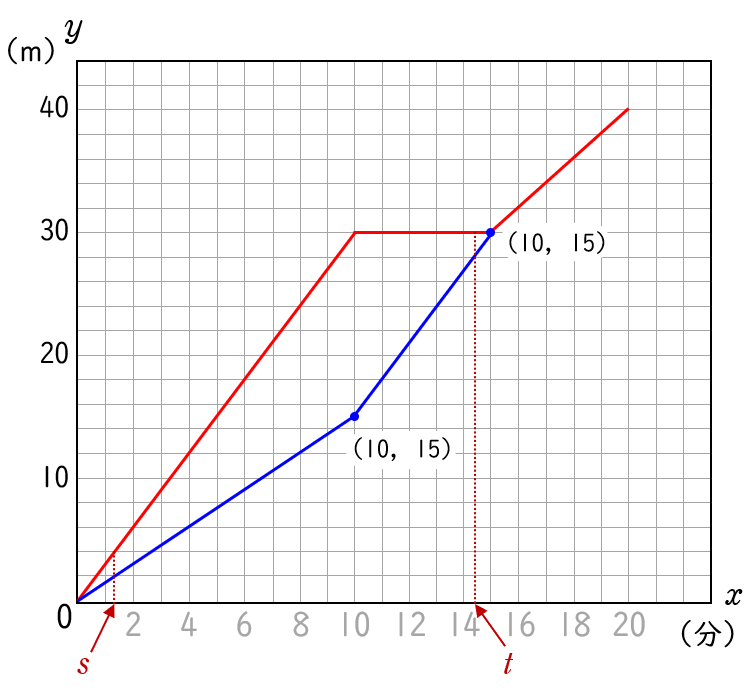
青線のグラフの式は,
$\,\,0≦x≦10\;\;$ のとき $\;y=1.5x$
$10≦x≦15\;$ のとき $\;y=3x-15$
$0≦x≦10$ の範囲において,赤線のグラフの式は $y=3x$ だから,
この範囲において,給水開始 $s$ 分後のことを考えると,
$A$ 側の水面の高さは, $3s$ cm,
$B$ 側の水面の高さは, $1.5s$ cm,
水面の高さの差は, $3s-1.5s=1.5s$ (cm)
よって,差が $2$ cm になるのは,
$1.5s=2$
$s=\dfrac{4}{\;3\;}$
$=1\dfrac{1}{\;3\;}$ (分)
$=1$ 分 $20$ 秒
また,$10≦x≦15$ の範囲において,給水開始 $t$ 分後のことを考えると,
$A$ 側の水面の高さは, $30$ cmのまま,
$B$ 側の水面の高さは, $3t-15$ cm,
水面の高さの差は, $30-(\,3t-15\,)=-3t+45$ (cm)
よって,差が $2$ cm になるのは,
$-3t+45=2$
$t=\dfrac{\;43\;}{3}$
$=14\dfrac{1}{\;3\;}$ (分)
$=14$ 分 $20$ 秒
5下の図で,△ ABC は ∠BAC $=90$° の直角三角形であり,△ ADE は ∠DAE $=90$° の直角三角形である。また,点 D は辺 CB の延長線上にある。
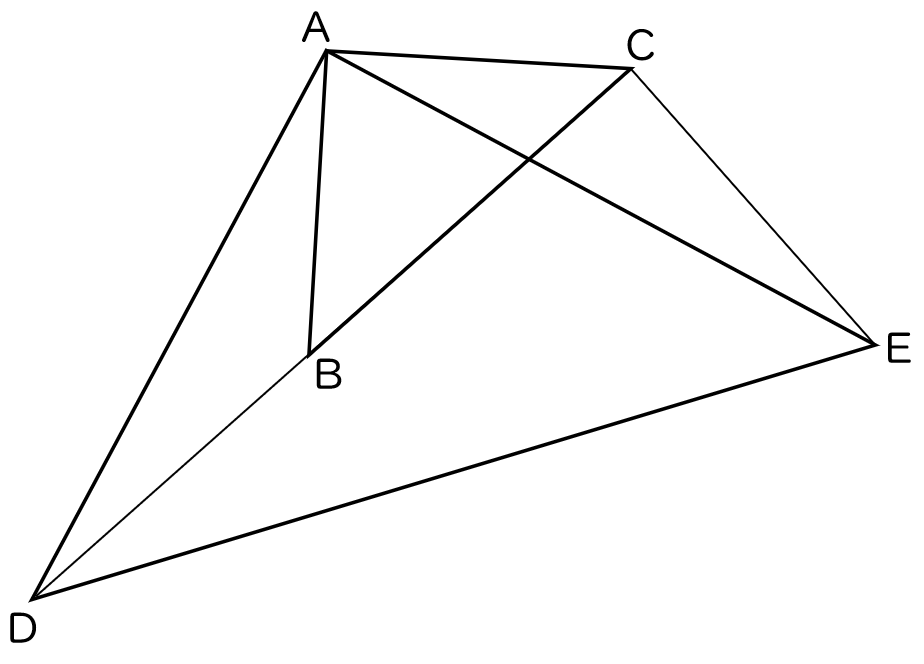
次の (1),(2) の問いに答えなさい。
(1)△ADB ≡ △AEC であることを証明しなさい。
解答
〈仮定〉AB $=$ AC,AD $=$ AE,∠BAC $=$ ∠DAE $=90$°
〈結論〉△ADB ≡ △AEC
〈証明〉
△ADB と △AEC で,
仮定から,AD = AE・・・・・・①
仮定から,AB = AC・・・・・・②
仮定から,∠DAE = ∠BAC = $90$°・・・・・・③
また,∠DAB = ∠DAE - ∠BAE・・・・・・④
∠EAC = ∠BAC - ∠BAE・・・・・・⑤
③,④,⑤ から,∠DAB = ∠EAC・・・・・・⑥
①,②,⑥ から,$2$ 組の辺とその間の角がそれぞれ等しいので,
△ADB ≡ △EBF
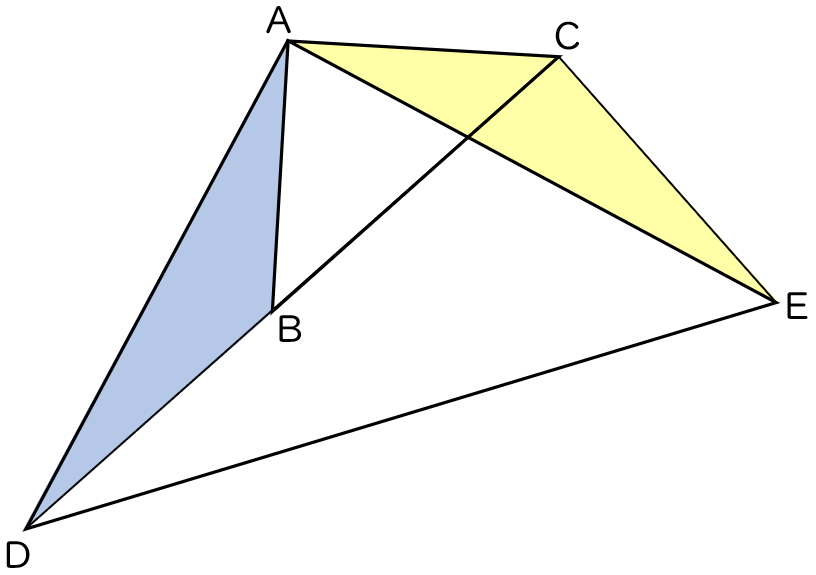
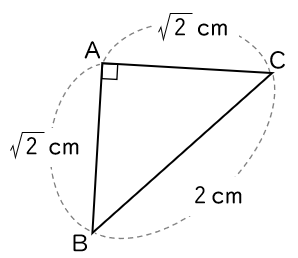
(2)AB $=$ OA $=\sqrt{\,2\,}$ cm,AD $=$ AE $=3$ cm のとき,
(ア)DE の長さを求めなさい。
解答・解説
解答$3\sqrt{\,2\,}$ cm
△ ABC は ∠BAC $=90$° の直角三角形だから,
AD:AE:DE $=$ $1$:$1$:$\sqrt{\,2\,}$
$3$:DE $=$ $1$:$\sqrt{\,2\,}$
DE $\times 1=3\times \sqrt{\,2\,}$
DE $=3\sqrt{\,2\,}$ (cm)
(イ)で必要なので,BC の長さも求めておきます。
△ ADE は ∠DAE $=90$° の直角三角形だから,
AB:AC:BC $=$ $1$:$1$:$\sqrt{\,2\,}$
$\sqrt{\,2\,}$:BC $=$ $1$:$\sqrt{\,2\,}$
BC $\times 1=\sqrt{\,2\,}\times \sqrt{\,2\,}$
BC $=2$ (cm)
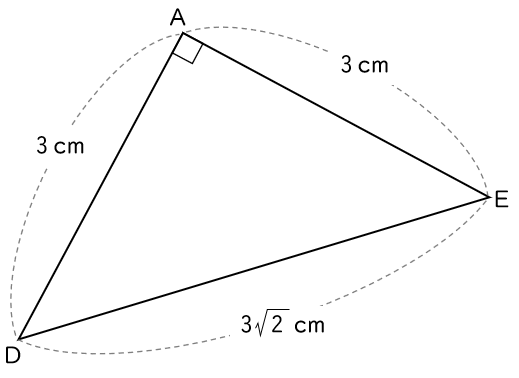
(イ)BD の長さを求めなさい。
解答・解説
解答$-1+2\sqrt{\,2\,}$ (cm)
(ア) から,BC $=2$ (cm) です。
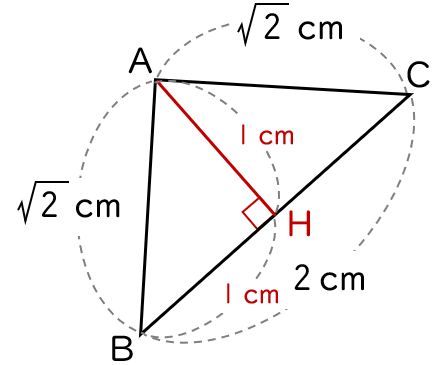
∠A の二等分線と辺 BC の交点を 点 H とすると,
二等辺三角形の頂角の二等分線は底辺を垂直に二等分するから,
∠AHB $=90$°,BH $=$ CH $=1$ (cm) です。
また,∠HBA $=45$° だから △ HAB も直角二等辺三角形です。
よって,AH $=1$ (cm) です。
△ADH について考えます。
∠AHD $=90$° だから,△ADH は直角三角形です。
BD $=x$ (cm) とすると,三平方の定理から,
AH$^{2}+$ DH$^{2} =$ AD$^{2}$
$1^{2}+(\,x+1\,)^{2}=3^{2}$
$1+x^{2}+2x+1=9$
$x^{2}+2x-7=0$
$x=\dfrac{\;-2\pm\sqrt{\,2^{2}-4\times 1\times (-7)\,}\;}{2}$
$=\dfrac{\;-2\pm\sqrt{\,32\,}\;}{2}$
$=\dfrac{\;-2\pm4\sqrt{\,2\,}\;}{2}$
$=-1\pm 2\sqrt{\,2\,}$
$x>0$ だから, $x=-1+ 2\sqrt{\,2\,}$
よって,BD $=-1+ 2\sqrt{\,2\,}$ (cm)
別 解
仮定から,∠ACB $=$ ∠AED $=45$°
よって,円周角の定理の逆から,
$4$ 点 A,D,E,C は同一円周上にあります。
その円を円O (中心が点 O) とします。
∠DAE は 弧DE に対する円周角で,∠DAE $=90$° だから,
弧DE に対する中心角は $180$° になり,
弦DE が直径であることが分かります (下の図のようになります)。
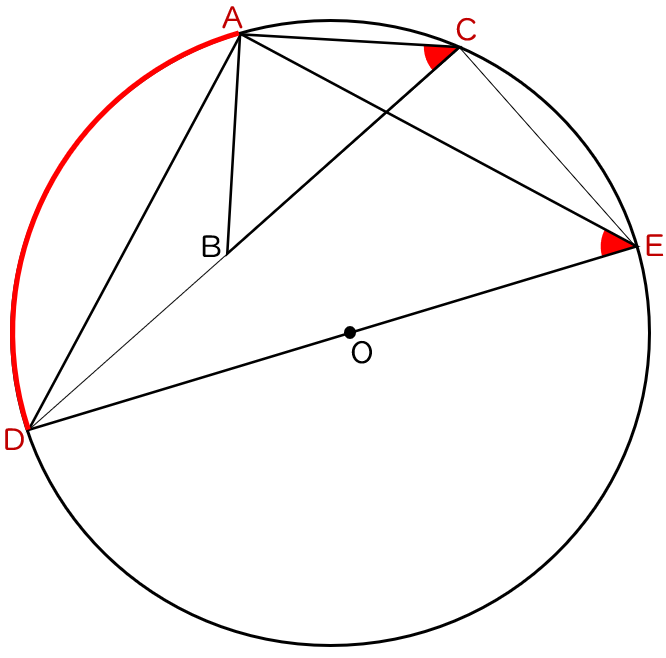
半円の弧に対する円周角だから,∠DCE $=90$° で,
△CDE は直角三角形です。
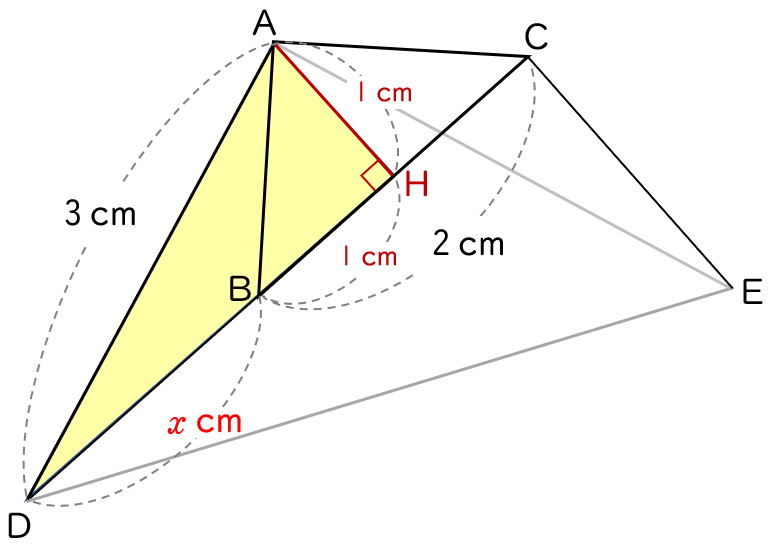
BD $=x$ (cm) とすると,
△ADB ≡ △AEC だから,CE $=x$ (cm) となり,
さらに,これまでのことから,下の図のようになります。
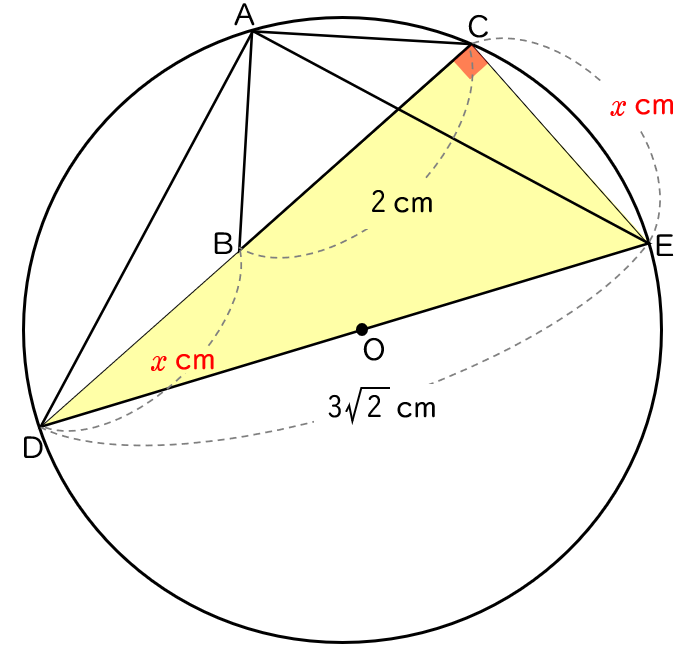
△CDE について三平方の定理から,
CD$^{2}+$ CE$^{2}=$ DE$^{2}$
$(\,x+2\,)^{2}+x^{2}=(3\sqrt{\,2\,})^{2}$
$x^{2}+2x-7=0$
$x=-1\pm 2\sqrt{\,2\,}$
$x>0$ だから, $\,\;x=-1+ 2\sqrt{\,2\,}$
よって,BD $=-1+ 2\sqrt{\,2\,}$ (cm)
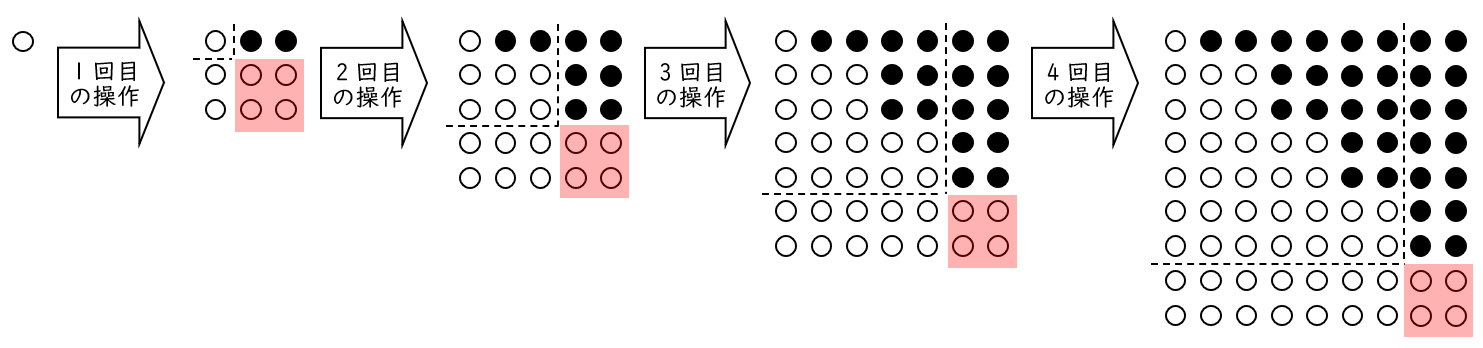
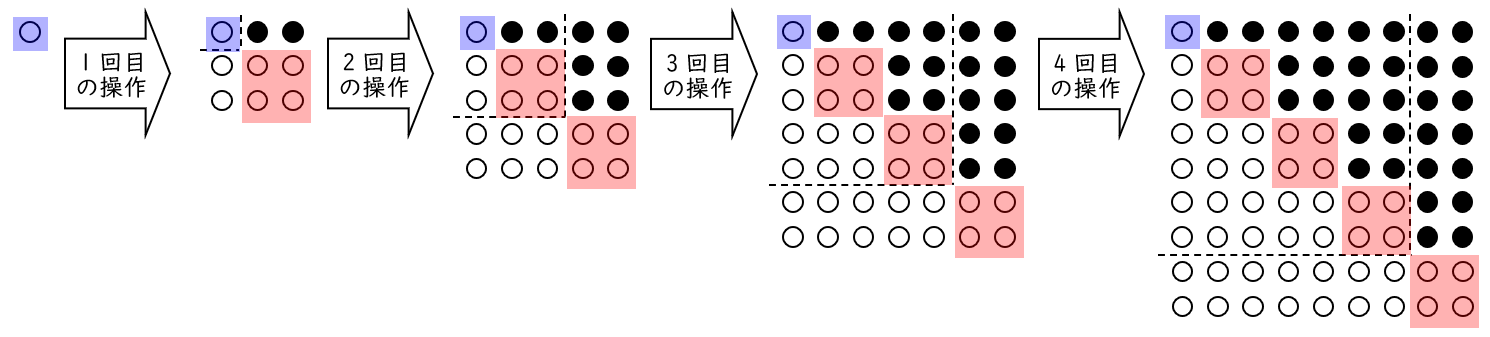
6平面上に,はじめ,白の碁石が $1$ 個置いてある。次の操作を繰り返し行い,下図のように,碁石を正方形状に並べていく。
【操作】すでに並んでいる碁石の右側に新たに黒の碁石を $2$ 列で並べ,次に,下側に新たに白の碁石を $2$ 段で並べる。

次の (1) ~ (4) の問いに答えなさい。
(1)4 回目の操作で,新たに並べる碁石について,
(ア)黒の碁石の数を求めなさい。
解答・解説
解答$14$ 個
図より,3 回目の操作の後の一辺の個数は $7$ 個です。
新たに並べる黒の碁石の数はこの $2$ 倍なので,
$7\times 2=14$ (個)
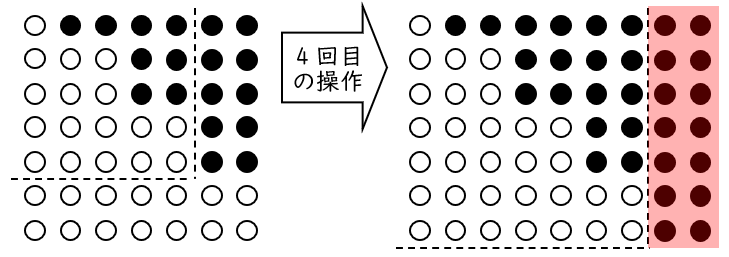
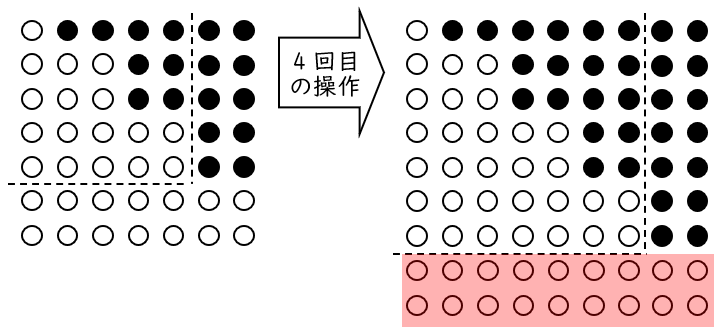
(イ)白の碁石の数を求めなさい。
解答・解説
解答$18$ 個
(ア)から,3 回目の操作の後,新たに黒の碁石を並べると,
横の一片は $7+2=9$ (個) になります。
新たに並べる白の碁石の数はこの $2$ 倍なので,
$9\times 2=18$ (個)
(2)$n$ 回目の操作を終えた後に,正方形状に並んでいる碁石の一辺の個数を,$n$ を使った式で表しなさい。
解答・解説
解答$2n+1$ (個)
一辺の個数を下の表に表します。
| 操作の回数 | 1 回目の後 | 2 回目の後 | 3 回目の後 | 4 回目の後 | ・ ・ ・ | $n$ 回目の後 |
|---|---|---|---|---|---|---|
| 一辺の個数 (個) | 3 | 5 | 7 | 9 | ・ ・ ・ | $\square$ |
一辺の個数は,1 回目の操作後が $3$ で,
その後,操作が 1 回終わるごとに $2$ 個ずつ増えていくと考えられます。
一辺の個数
1 回目後 ・・・ $3$ (個)
2 回目後 ・・・ $3+2\times \color{red}1$ (個)$=5$ (個)
3 回目後 ・・・ $3+2\times \color{red}2$ (個)$=7$ (個)
4 回目後 ・・・ $3+2\times \color{red}3$ (個)$=9$ (個)
・
・
・
$n$ 回目後 ・・・ $3+2\times \color{red} (\,n-1\,)$ (個)
上のように考えると,
$n$ 回目の後は 1 回目の後の個数に $2$ 枚を $(\,n-1\,)$ 回足した数になります。
よって,$n$ 回目の操作後の一片の個数は,
$3+2\times (\,n-1\,)=3+2n-2$
$=2n+1$ (枚)
(3)次の文章は,$n$ 回目の操作を終えた後に並んでいる碁石の個数について,花子さんの考えをまとめたものである。ア には数を,イ,ウ,エ には $n$ を使った式を,それぞれあてはまるように書きなさい。
はじめ,白の碁石が $1$ 個だけ置いてある。また,$1$ 回の操作で新たに並べる白の碁石の個数は,新たに並べる黒の碁石の数より ア 個多い。
解答・解説
解答ア$\quad4$
1 回の操作で新たに並べる白の碁石と黒の碁石の個数を比べると,
下の図から白の碁石の方が $4$ 個多いことが分かります。
したがって,$n$ 回目の操作を終えた後に並んでいる黒の碁石の個数を $A$ 個とすると,白の碁石の個数は,$(\,1+A+$ イ $)$ 個と表すことができる。
解答・解説
解答イ$\quad4n$
白の碁石の個数は,
はじめの $1$ 個とその後新たに並べられた個数の和になります。
以下,白の碁石の個数を「白の数」,
黒の碁石の個数を「黒の数」と表します。
1 回の操作で増える白の数は,
1 回の操作で増える黒の数より $4$ 個多いので,
$n$ 回後には,それまでに並んだ黒の総数より $4\times n=4n$ (個) 多く並ぶ
ことになります。
よって,$n$ 回目の操作後の白の総数は,
はじめの$1$ 個 $+$ 黒の総数 $+$ $4n=1+A+4n$ (個)
また,$n$ 回目の操作を終えた後に,正方形状に並んでいる碁石の総数は,ウ 個である。
解答・解説
解答ウ$\quad(\,2n+1\,)^{2}\quad$ または $\quad 4n^{2}+4n+1$
(2) から,$n$ 回目の操作を終えた後の一辺の個数は,$(¥,2n+1¥,)$ 個です。
よって,$n$ 回目の操作を終えた後の碁石の総数は,
$(\,2n+1\,)\times (\,2n+1\,) = (\,2n+1\,)^{2}$ (個)
これらのことから,方程式をつくると,
$A+(\,1+A+$ イ $)=$ ウ
となる。これを解くと,$A=$ エ となる。
よって,$n$ 回目の操作を終えた後に並んでいる黒の碁石の数は,エ 個となる。
解答・解説
解答ウ$\quad 2n^{2}$
$n$ 回目の操作を終えた後の碁石の総数についての方程式は,
$A+(\,1+A+4n\,)=(\,2n+1\,)^{2}$
$2A+4n+1=4n^{2}+4n+1$
$A=2n^{2}$
(4)20 回目の操作を終えた後に並んでいる白の碁石の個数を求めなさい。
解答・解説
解答$881$ 個
白の碁石の個数を「白の数」,
黒の碁石の個数を「黒の数」と表します。
(3) から,
$n$ 回目の操作後の黒の数は $2n^{2}$ (個)だから,
20 回目の操作後の黒の数は,
$2\times 20^{2}=800$ (個)
(3) から,
$n$ 回目の操作後の黒の数を $A$ 個とすると,
$n$ 回目の操作後の白の数は $(\,1+A+4n\,)$ 個だから,
20 回目の操作後の白の数は,
$1+800+4\times 20=881$ (個)

