岐阜県・公立高校入試 2019年度( 平成31年度 )解答・解説編
岐阜県立高校・入学試験学力検査・数学・2019年度
1次の(1)~(6)の問いに答えなさい。
(1)$10-4^{2}\;\;$を計算しなさい。
解答・解説
解答$-6$
$10\;\color{red}{-\;4^{2}}$$-4^{2}=-(4\times 4)=-16$
$=10-16$
$=-6$
(2)$4(\,2a+b\,)-2(\,a-3b\,)\;\;$を計算しなさい。
解答・解説
解答$16a$
$4(\,2a+b\,)-2(\,a-3b\,)$
$=\color{red}4\color{black}\times 2a \color{red}+4\color{black}\times b\color{red}-2\color{black}\times a\color{red}-2\color{black}\times (-3b)$
$=8a+4b-2a\bf\color{red}+\rm\color{black}6\it b$
$=8a-2a+4b+6b$
$=6a+10b$
(3)$x=\sqrt{\,2\,}+3\quad$のときの,式$\quad x^{2}-6x+9\quad$の値を求めなさい。
解答・解説
解答$2$
値を求める式は,
$x^{2}-6x+9=(\;x-3\;)^{2}$
と変形できるので,この式に $x=\sqrt{\,2\,}+3\quad$ を代入します。
$x^{2}-6x+9=(\;x-3\;)^{2}$
$=(\;\color{red}\sqrt{\,2\,}+3\color{black}-3\;)^{2}$
$=(\;\sqrt{\,2\,}\;)^{2}$
$=2$
(4)ある養殖池にいるアユの数を推定するために,その養殖池で $47$ 匹のアユを捕獲し,その全部に目印をつけて戻した。数日後に同じ養殖池で $27$ 匹のアユを捕獲したところ,目印のついたアユが $3$ 匹いた。この養殖池にいるアユの数を推定し,十の位までの概数で求めなさい。
解答・解説
解答およそ $420$ 匹
養殖池にいるアユの総数を $x$ 匹とする。
「養殖池にいるアユの総数 ($x$)」に対する「目印をつけたアユの数 ($47$)」の割合
と,
「捕獲したアユの数 ($27$)」に対する「その中の目印のついたアユの数 ($3$) 」の割合
は等しいと推定されるから,
$x:47=27:3$
という比例式が成り立ちます。
$x:47=\color{red}\cancelto{9}{\color{black}27}\color{black}:\color{red}\cancelto{1}{\color{black}3}$
$x=47\times 9$
$x=423$
一の位を四捨五入して,およそ $420$ 匹だと推定できます。
(5)関数 $y=4x+5$ について述べた文として正しいものを,次のア~エの中からすべて選び,符号で答えなさい。
アグラフは点 $(\;4,\;5\;)$ を通る。
イグラフは右上がりの直線である。
ウ$x$ の値が $-2$ から $1$ まで増加するときの $y$ の増加量は $4$ である。
エグラフは,$y=4x$ のグラフを,$y$ 軸の正の向きに $5$ だけ平行移動させたものである。
解答・解説
解答イ,エ
関数 $y=4x+5$ は 1 次関数( $y$ は $x$ の 1 次関数である)だから,
変化の割合は一定で,グラフは直線になります。
ア について
グラフが点 $(\;4,\;5\;)$ を通るとは,$x=4$ のとき $y=5$ になることです。
$y=4x+5$ に $x=4$ を代入すると,
$y=4\times 4+5=21$
となり,正しくないことが分かります。
イ について
グラフが右上がりの直線であるとは,傾き(=変化の割合)が常に正の値であることです。
$y=4x+5$ の傾きは $4$ で常に正の値だから,グラフは常に右上がりとなります。
よって正しいといえます。
ウ について
変化の割合は一定で,その値は $4$ です。
よって,$x$ の値が $1$ ずつ増加すると,$y$ の値は $4$ ずつ増加します。
これは,$y$ の増加量は常に $x$ の増加量の $4$ 倍であることを意味します。
$x$ の値が $-2$ から $1$ まで増加するとき,その増加量は
$1-(-2)=3$
です。このとき $y$ の増加量はその $4$ 倍だから,
$3\times 4=12$
となり,正しくないことが分かります。
また,変化の割合 $=\dfrac{\;y\,\sfの増加量\;}{x\,\sfの増加量}$ より,
$4=\dfrac{ y\,\sfの増加量 }{1-(-2)}$
$y$ の増加量 $=4 \times 3 = 12$
となり,これからも正しくないことが分かります。
エ について
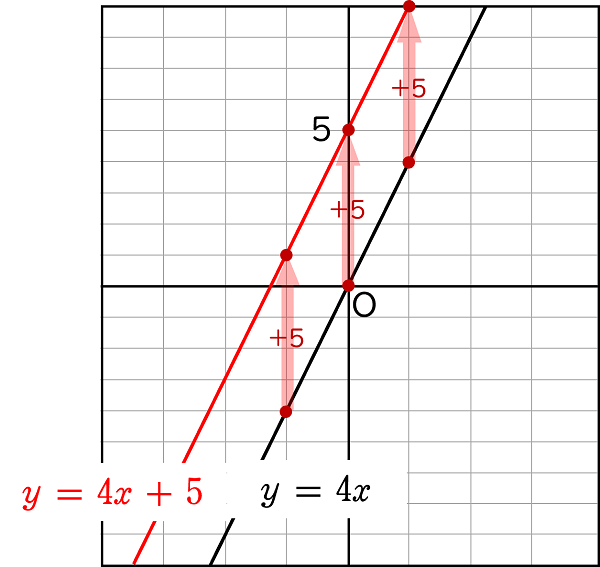
$y=4x+5$ ・・・① のグラフと $y=4x$ ・・・② のグラフは,
傾きが同じなので平行です。
実際のグラフは下図のようになり,各グラフ上の $x$ 座標が同じ点をみると,
①の点の $y$ 座標は,②の点の $y$ 座標より $5$ 大きくなっています。
よって,$y=4x+5$ のグラフは,
$y=4x$ のグラフを,$y$ 軸の正の向きに $5$ だけ平行移動させたものであり,
正しいといえます。
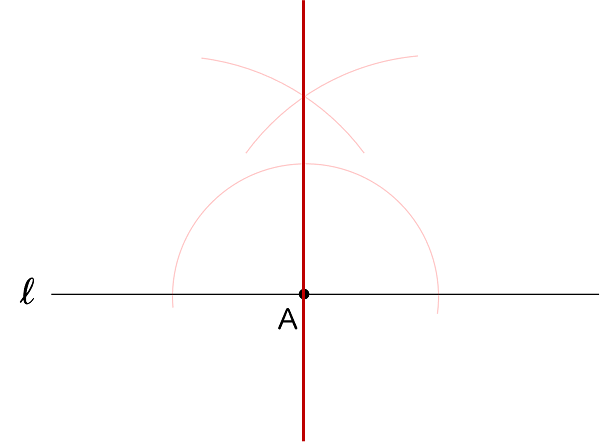
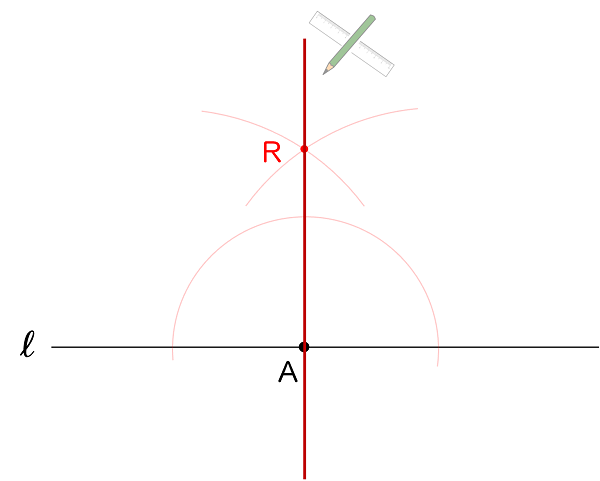
(6)直線 $\ell$ 上の点 A を通り,直線 $\ell$ に垂直な直線を,定規とコンパスを使って作図しなさい。なお,作図に用いた線は消さずに残しなさい。

解答・解説
解答
作図の手順
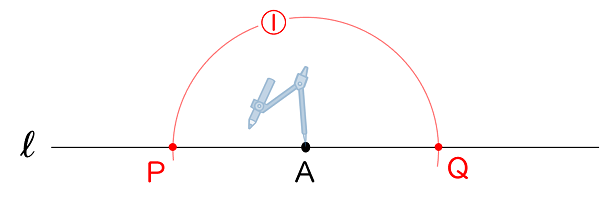
① 下図のように,コンパスで点 A を中心とした円をかき,点 P,Q を決めます。
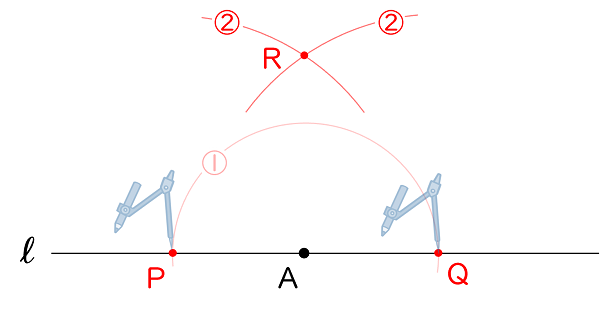
② 下図のように点 P を中心とした円(弧)と点 Q を中心とした円(弧)をかき,点 R を決めます。
③ 点 A と 点 R を通る直線をかきます。この直線が求める直線です。
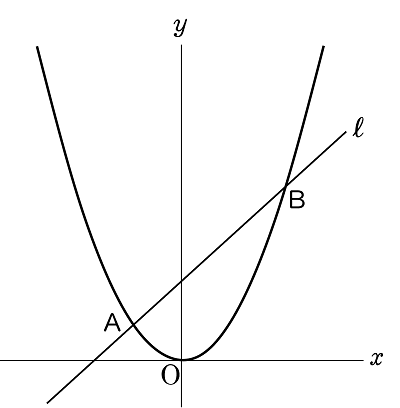
2右の図のように,関数 $y=ax^{2}$ のグラフと直線 $\ell$ が,$2$ 点 A,B で交わっている。A の座標は $(\;-1,\;2\;)$ で,B の $x$ 座標は $2$ である。
次の (1) ~ (3) の問いに答えなさい。
(1)$a$ の値を求めなさい。
解答・解説
解答2
関数 $y=ax^{2}$ のグラフ上に点 A $(\,-1,\;2\,)$ があるから,
$x=-1$,$y=2$ は $y=ax^{2}$ を成り立たせます。
$y=ax^{2}$ に $x=-1$,$y=2$ を代入して,
$2=a\times (-1)^{2}$
$a=2$
(2)直線 $\ell$ の式を求めなさい。
解答・解説
解答$y=2x+4$
(1) から,グラフが放物線である関数の式は $y=2x^{2}$ です。
点 B は $y=2x^{2}$ 上にあり,$x$ 座標が $2$ だから,$y$ 座標は,
$y=2\times 2^{2}=8$
よって,点 B の座標は $ (\;2,\;8\;) $
直線 $\ell$ は $x$ 軸に対し垂直でない直線だから,1 次関数のグラフです。
直線 $\ell$ の式を $y=ax+b$ と表します。
2 点 A,B は 直線 $\ell$ 上にあり,変化の様子は下の表のようになります。
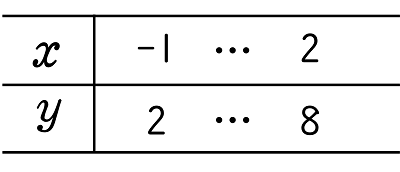
表の $-1≦x≦2$ の範囲について,
$a=\dfrac{8-2}{\;2-(-1)\;}=2$
よって,求める式は $\;y=2x+b$ となり,
さらに,$y=2x+b$ に $x=-1$,$y=2$ を代入して,
$2=2\times (-1)+b$
$2=-2+b$
$b=4$
したがって,求める式は $y=2x+4$ です。
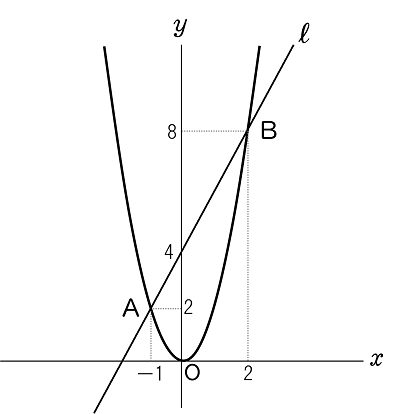
グラフの様子は下の図ようになります。
(3)△AOB の面積を求めなさい。
解答・解説
解答$6$
(2) から, 直線 $\ell$ の式は $y=2x+4$ で,切片は $4$ だから,
直線 $\ell$ と $y$ 軸との交点を点 C とすると,その座標は $(\,0,\;4\,)$ です。
下の図のように △AOB を △AOC と △BOC に分けて考えます。
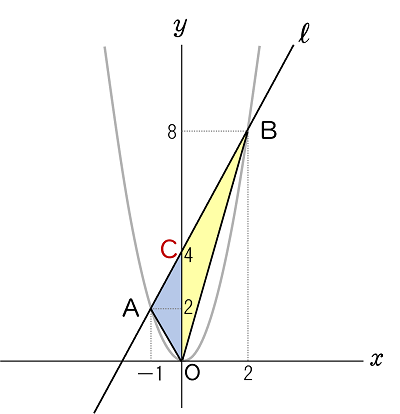
△AOC は底辺を辺 OC とすると,高さは $1$ になるから,その面積は,
$4\times 1 \times \dfrac{1}{\;2\;}=2$
△BOC は底辺を辺 OC とすると,高さは $2$ になるから,その面積は,
$4\times 2 \times \dfrac{1}{\;2\;}=4$
よって,
△AOB $=$ △AOC $+$ △BOC
$=2+4$
$=6$
別 解
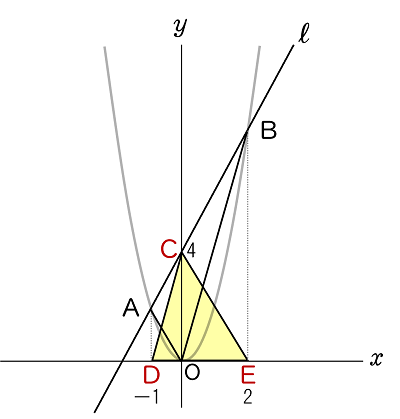
下の図のように点D $(\,-1,\;0\,)$ と点E $(\,2,\;0\,)$ をとり,
△AOB を等積変形した △CDE の面積を求めても良い。
3右の図のように,袋の中に,赤玉 2 個と白玉 2 個が入っている。それぞれの色の玉には,1,2 の数字が $1$ つずつ書かれている。玉をかき混ぜてから $1$ 個取り出し,それを袋に戻してかき混ぜ,また $1$ 個取り出すとき,次の (1) ~ (2) の問いに答えなさい。
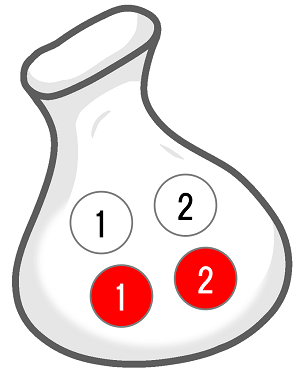
(1)$2$ 回とも白玉が出る確率を求めなさい。
解答・解説
解答$\dfrac{1}{\;4\;}$
取り出し方のすべての場合を樹形図(下の図)で表します。
全ての場合の数は,$4\times4=16$ (通り)です。
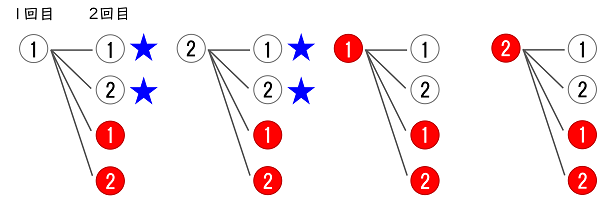
$2$ 回とも白玉が出る場合は,上の図の★の $4$ 通りです。
その確率は,
$\dfrac{4}{\;16\;}=\dfrac{1}{\;4\;}$
(2)$2$ 回とも同じ色の玉が出る確率を求めなさい。
解答・解説
解答$\dfrac{1}{\;2\;}$
取り出し方のすべての場合を樹形図(下の図)で表します。
全ての場合の数は,$4\times4=16$ (通り)です。
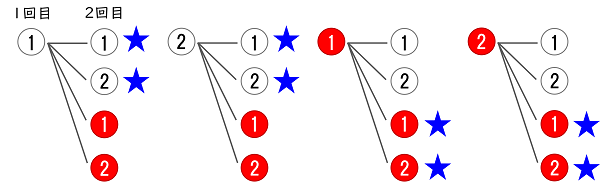
$2$ 回とも同じ色の玉が出る場合は,上の図の★の $8$ 通りです。
その確率は,
$\dfrac{8}{\;16\;}=\dfrac{1}{\;2\;}$
(3)$1$ 回目と $2$ 回目で,色も数字も異なる玉が出る確率を求めなさい。
解答・解説
解答$\dfrac{1}{\;4\;}$
取り出し方のすべての場合を樹形図(下の図)で表します。
全ての場合の数は,$4\times4=16$ (通り)です。
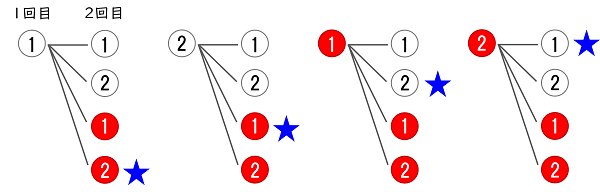
$1$ 回目と $2$ 回目で,色も数字も異なる玉が出る場合は,上の図の★の $4$ 通りです。
その確率は,
$\dfrac{4}{\;16\;}=\dfrac{1}{\;4\;}$
4ある工場では,機械 A と機械 B をそれぞれ $1$ 台ずつ使って,製品 P と製品 Q を作っている。それぞれの機械は,どちらの製品も作ることができるが,両方の製品を同時につくることはできない。
A だけを使って Q だけを作ると,P だけをつくるときに比べて,$1$ 時間につくることができる製品の個数は $2$ 割多い。また,B を使って Q だけを作ると,P だけを作るときに比べて $1$ 時間につくることができる製品の個数は $1$ 割少ない。
A と B の両方を使って,P だけを作ると $1$ 時間に $55$ 個でき,Q だけを作ると $1$ 時間に $57$ 個できる。
次の (1),(2) の問いに答えなさい。
(1)A と B のうち,どちらか $1$ 台を使って $1$ 時間に作ることができる製品の個数を,太郎さんは次のように求めた。ア には $x$ を使った式を,イ には $y$ を使った式を,ウ ~ カ にはそれぞれあてはまるように書きなさい。
A を使って $1$ 時間に作ることができる製品の個数について,P だけを作るときを $x$ 個とすると,Q だけを作るときは $2$ 割多いので ア 個と表すことができる。
また,B を使って $1$ 時間に作ることができる製品の個数について,P だけを作るときを $y$ 個とすると,Q だけを作るときは $1$ 割少ないので イ 個と表すことができる。
$1$ 時間に作ることができる製品の個数から連立方程式をつくると,
$\;\left\{\begin{array}{l}\;\quad\, x \quad\, + \quad\; y \quad\,=55\\ \;\sf\framebox[1.5cm][c]{ア}+\framebox[1.5cm][c]{イ}=\rm 57\end{array}\right.\;$
となる。これを解くと,$x=$ ウ,$y= $エ となる。
よって,A と B のうち,どちらか1台を使って1時間に作ることができる製品の個数は,下の表のようになる。
| A | B | |
| P だけを作るとき(個) | ウ | エ |
| Q だけを作るとき(個) | オ | カ |
解答・解説
解答ア $1.2x$ イ $0.9x$ ウ $25$ エ $30$ オ $30$ カ $27$
A で $1$ 時間に作ることができる P の個数を $x$ 個とすると,
A で $1$ 時間に作ることができる Q の個数は,
$x$ 個より $2$ 割多いから,
$x \times (\;1+0.2\;)=1.2x$ (個)ア$1.2x$
です。
B で $1$ 時間に作ることができる P の個数を $y$ 個とすると,
B で $1$ 時間に作ることができる Q の個数は,
$y$ 個より $1$ 割少ないから,
$y \times (\;1-0.1\;)=0.9y$ (個)イ$0.9y$
です。
A と B 両方使って,P だけを作ると $1$ 時間に $55$ 個できるから,
$x+y=55$
A と B 両方使って,Q だけを作ると $1$ 時間に $57$ 個できるから,
$1.2x+0.9y=57$
これらから,次の連立方程式ができます。
$\;\left\{\begin{array}{l}\quad\;\: x + \quad\; y=55\;\cdots①\\ \;1.2x + 0.9y=57\;\cdots②\end{array}\right.\;$
② を変形して,$4x+3y=190 \;\cdots②'$
$①\times 4$ $4x+4y=220$
$②'$$\;-)\;4x+3y=190\;$
$y=30$エ$30$
$y=30$ を $①$ に代入して,
$x+30=55$
$x=25$ウ$25$
また,
$1.2x=1.2\times 25=30$オ$30$
$0.9y=0.9\times 30=27$カ$27$
方程式 ② の変形
$1.2x+0.9y=57$両辺に $10$ をかける
$12x+9y=570$両辺を $3$ で割る
$4x+3y=190$
(2)別の工場では,A と B をそれぞれ複数台使って,Q だけを $1$ 時間に $600$ 個作っている。このとき,A の台数を全て求めなさい。
解答・解説
解答$2$ 台,$11$ 台
(1) から,Q だけを作る場合,
A $1$ 台で $1$ 時間に作ることができるのは $30$ 個
B $1$ 台で $1$ 時間に作ることができるのは $27$ 個
です。
A を $a$ 台,B を $b$ 台使って,Q だけを $600$ 個作っているとすると,
$30a+27b=600$
$30a=600-27b$
$a=20-\dfrac{9}{\;10\;}b$
B だけを使って Q を $1$ 時間に $600$ 個作ることはできないので,
$a$ は $1$ 以上の整数です。
$20-\dfrac{9}{\;10\;}b$ が $1$ 以上の整数だから,$b$ は $10$ の倍数です。
$b$ が $10$ のとき,$a=20-\dfrac{9}{\;10\;}\times 10=11$
$b$ が $20$ のとき,$a=20-\dfrac{9}{\;10\;}\times 20=2$
$b$ が $30$ 以上のとき,$a$ は 負の数になってしまうので不適切です。
よって,A の台数は $2$ 台または $11$ 台です。
5下の図のように,四角形 ABCD の $4$ つの頂点 A,B,C,D が円 O の周上にある。線分 AC と BD の交点を E とする。また,E を通り辺 BC と平行な直線と辺 AB との交点を F とする。
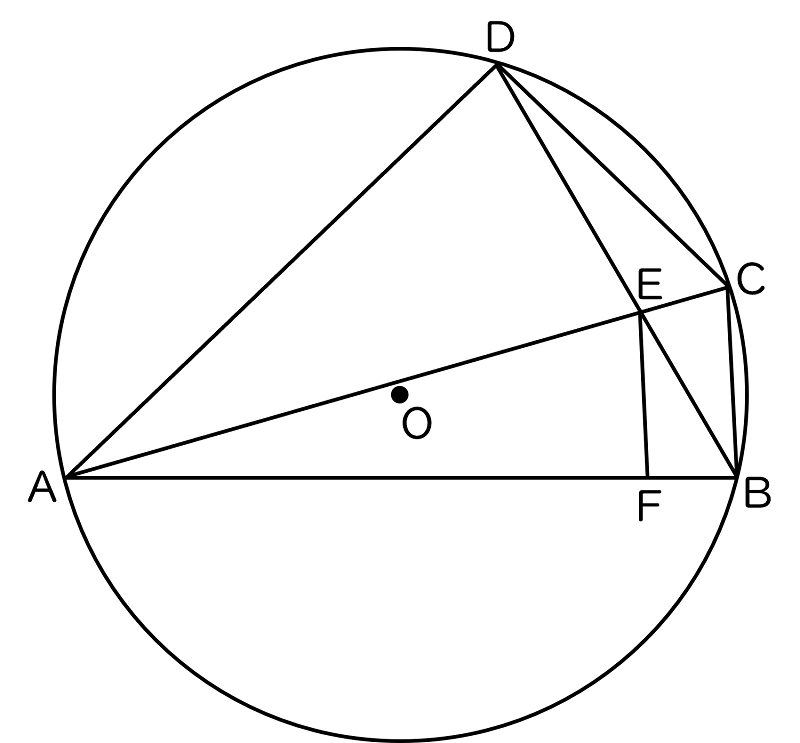
次の (1),(2) の問いに答えなさい。
(1)△ACD ∽ △EBF であることを証明しなさい。
解答
〈仮定〉点A,B,C,Dが円O の円周上にある
BC $/\!/$ FE
〈結論〉△ACD ∽ △EBF
〈証明〉
△ACD と △EBF で,
$\stackrel{\Large\frown}{\small\sf AD}$ に対する円周角だから,
∠ACD = ∠EBF・・・・・・①
$\stackrel{\Large\frown}{\small\sf CD}$ に対する円周角だから,
∠CAD = ∠EBC・・・・・・②
BC $/\!/$ FE より,平行線の錯角だから,
∠BEF = ∠EBC・・・・・・③
②,③ から,∠CAD = ∠BEF・・・・・・④
①,④ から,2 組の角がそれぞれ等しいので,
△ACD ∽ △EBF
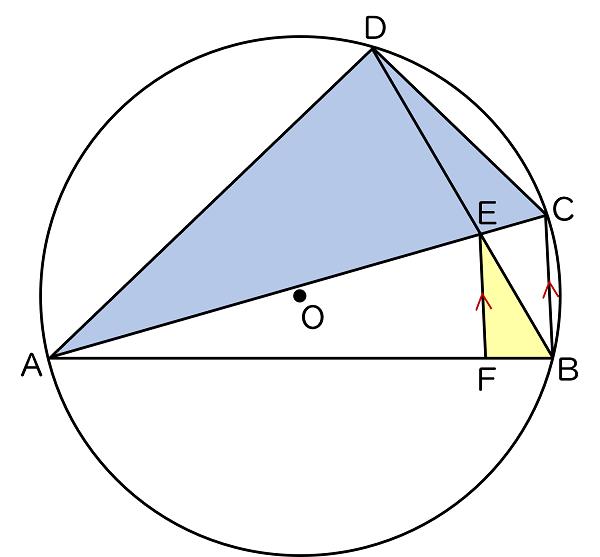
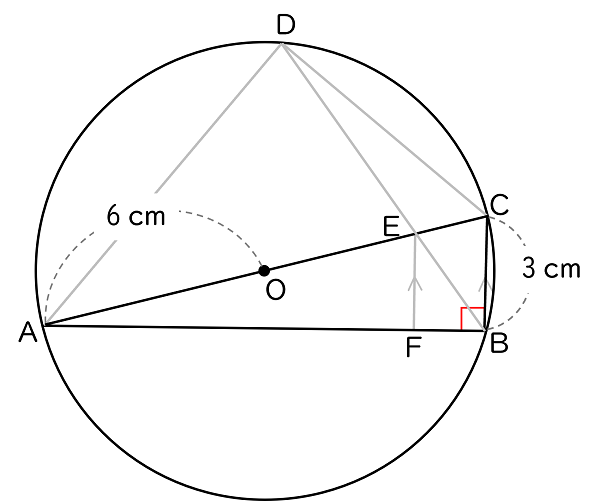
(2)AC が円 O の直径で,OA $=6$ cm,BC $=3$ cm,CE $=2$ cm のとき,
(ア)AB の長さを求めなさい。
解答・解説
解答$3\sqrt{\,15\;}$ cm
仮定から,図は右のようになります。
半円の弧に対する円周角だから,
∠ABC $=90$°
よって,△ABC は直角三角形です。
また,OA $=6$ cm で AC は円 O の直径だから,
AC $=12$ cm
△ABC について三平方の定理から,
AB $=\sqrt{\small\;\sf AC^{2}-BC^{2}\;}$
$=\sqrt{12^{2}-3^{2}}$
$=\sqrt{\;135\;}$
$=3\sqrt{\,15\;}$
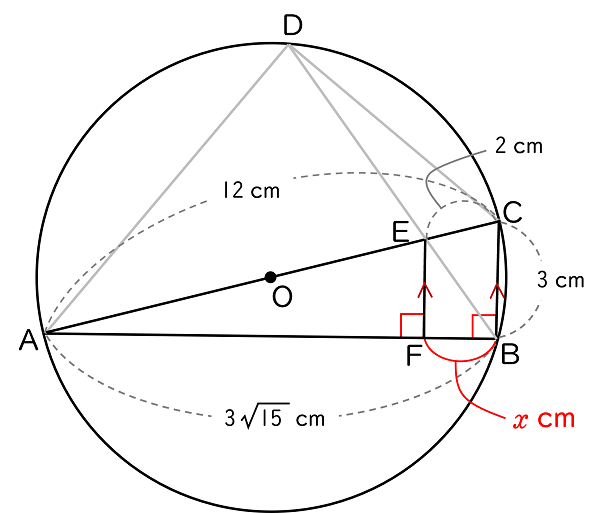
(イ)BF の長さを求めなさい。
解答・解説
解答$\dfrac{\;\sqrt{\,15\,}\;}{2}$ cm
仮定から,図は右のようになります。
BF $=x$ cm とします。
仮定から BC $/\!/$ FE だから,△ABC について,
$\sf AE:EC=AF:FB$
$(\,12-2\,)\sf:\rm 2=(\, 3\sqrt{\,15\;}-\it x\,\rm)\sf:\it x$
$5\sf:\rm 1=(\, 3\sqrt{\,15\;}-\it x\,\rm)\sf:\it x$
$5x=3\sqrt{\,15\;}-x$
$6x=3\sqrt{\,15\;}$
$x=\dfrac{\;\sqrt{\,15\,}\;}{2}$ (cm)
更に,FE $=y$ cm とすると,
$\sf AC:AE=BC:FE$
$12\sf:\rm (\,12-2\,)=3\sf:\it y$
$6\sf:\rm 5=3\sf:\it y$
$6y=15$
$y=\dfrac{5}{\;2\;}$ (cm)
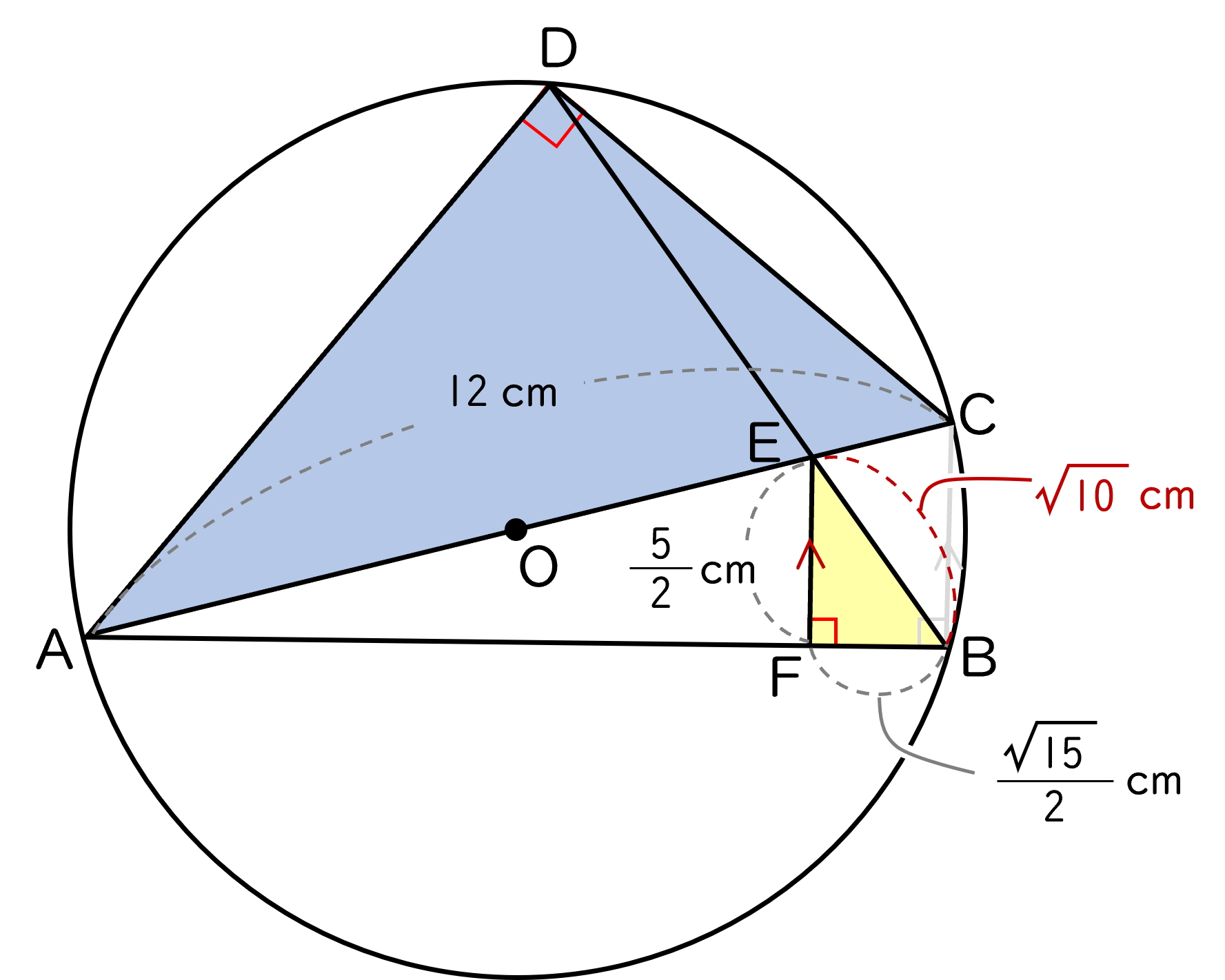
(ウ)△ACD の面積を求めなさい。
解答・解説
解答$9\sqrt{\,15\,}$ cm$^{2}$
(イ) から,BF $=\dfrac{\;\sqrt{\,15\,}\;}{2}$ cm,FE $=\dfrac{5}{\;2\;}$ cm
仮定から BC $/\!/$ FE ,(ア) から∠ABC $=90$°
平行線の同位角だから,∠ABC = ∠AFE $=90$°
すなわち ∠EFB $=90$° なので △EBF は直角三角形です。
まず,△EBF の面積を求めます。
△EBF $=\dfrac{1}{\;2\;}\times$BF$\times$FE
$=\dfrac{1}{\;2\;}\times \dfrac{\;\sqrt{\,15\,}\;}{2}\times \dfrac{5}{\;2\;} $
$=\dfrac{\;5\sqrt{\,15\,}\;}{8}$ (cm$^{2}$) $\quad\cdots①$
さらに,△EBF について三平方の定理から,
EB $=\sqrt{\small\;\sf BF^{2}+FE^{2}\;}$
$=\sqrt{\left(\dfrac{\;\sqrt{\,15\,}\;}{2} \right)^{2} +\left( \dfrac{5}{\;2\;} \right)^{2}\;}$
$=\sqrt{\;10\;}$ (cm)
△ACD ∽ △EBF で,その相似比は,
AC:EB $=$ $12$:$\sqrt{\,10\,}$
よって,△ACD と △EBF の面積比は,
$12^{2}$:$(\sqrt{\,10\,}\,)^{2}=144$:$10$
$=72$:$5$ $\quad\cdots②$
①,②から,
△ACD:△EBF $=72$:$5$
△ACD:$\dfrac{\;5\sqrt{\,15\,}\;}{8}=72$:$5$
△ACD $\times \color{red}\cancelto{1}{\color{black}5}\color{black}=\dfrac{\;\color{red}\cancelto{1}{\color{black}{5}}\color{black}\sqrt{\,15\,}\;}{\color{blue}\cancel{\color{black}8}\,^{1}} \times \color{blue}\cancelto{9}{\color{black}72}$
△ACD $=9\sqrt{\,15\,}$
6図 1 のように,$1$ 辺の長さが $1$ cm の正方形のカードをすき間なく並べて順番に図形を作る。段の数は,順に $1$ 段ずつ増やし,一番下の段のカードの枚数は,順に $2$ 枚ずつ増やす。
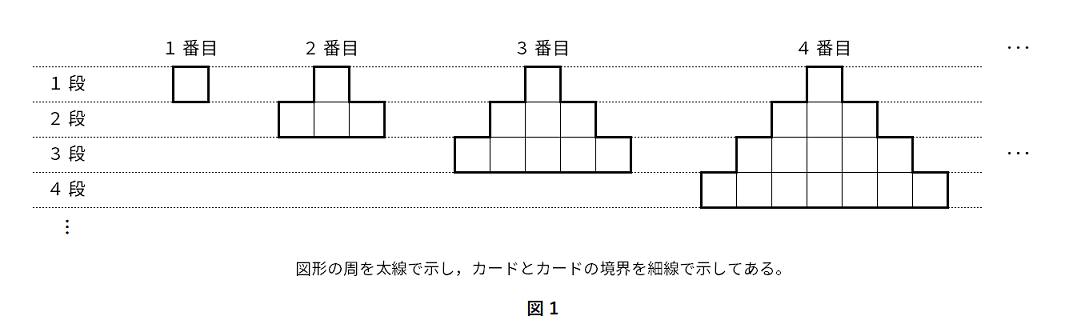
次の (1) ~ (4) の問いに答えなさい。
(1)5 番目の図形について,
(ア)一番下の段のカードの枚数を求めなさい。
解答・解説
解答$9$ 枚
一番下の段のカードの枚数を下の表に表します。
| 番 数 | 1 番目 | 2 番目 | 3 番目 | 4 番目 |
|---|---|---|---|---|
| 一番下の段のカードの枚数 (枚) | 1 | 3 | 5 | 7 |
一番下のカードの枚数は,
$1$ 枚から始まり,$2$ 枚ずつ増えています。
4 番目の一番下のカードが $7$ 枚なので,5 番目の一番下は,
$7+2=9$ (枚)
実際に 5 番目の図形をかいてみると下の図になります。
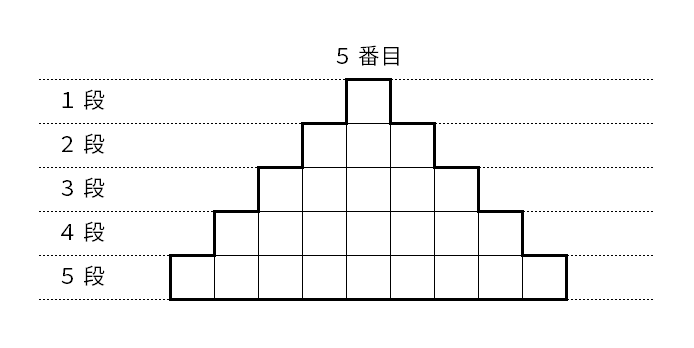
(イ)周の長さを求めなさい。
解答・解説
解答$28$ cm
周の長さを下の表に表します。
| 番 数 | 1 番目 | 2 番目 | 3 番目 | 4 番目 |
|---|---|---|---|---|
| 周の長さ (cm) | 4 | 10 | 16 | 22 |
周の長さは,
$4$ cm から始まり,$6$ cm ずつ増えています。
4 番目の図形の周長さが $22$ cmなので,5 番目の図形の周の長さは,
$22+6=28$ (cm)
実際に 5 番目の図形をかいてみると下の図になります。

(2)$n$ 番目の図形について,
(ア)一番下の段のカードの枚数を,$n$ を使った式で表しなさい。
解答・解説
解答$2n-1$ (枚)
一番下の段のカードの枚数を下の表に表します。
| 番 数 | 1 番目 | 2 番目 | 3 番目 | 4 番目 | ・ ・ ・ | $n$ 番目 |
|---|---|---|---|---|---|---|
| 一番下の段のカードの枚数 (枚) | 1 | 3 | 5 | 7 | ・ ・ ・ | $\square$ |
一番下の段のカードの枚数は,
1 番目の $1$ 枚に,番数が $1$ 増えるごとに $2$ ずつ足されていくと考えられます。
1 番下のカードの枚数
1 番目 ・・・ $1$ (枚)
2 番目 ・・・ $1+2\times \color{red}1$ (回)$=3$ (枚)
3 番目 ・・・ $1+2\times \color{red}2$ (回)$=5$ (枚)
4 番目 ・・・ $1+2\times \color{red}3$ (回)$=7$ (枚)
・
・
・
$n$ 番目 ・・・ $1+2\times \color{red} (n-1)$ (回)
上のように考えると,
$n$ 番目は 1 番目の枚数に $2$ 枚を $(\,n-1\,)$ 回足した数になります。
よって,$n$ 番目の図形の一番下のカードの枚数は,
$1+2\times (\,n-1\,)=1+2n-2$
$=2n-1$ (枚)
(イ)周の長さを,$n$ を使った式で表しなさい。
解答・解説
解答$6n-2$ (枚)
周の長さを下の表に表します。
| 番 数 | 1 番目 | 2 番目 | 3 番目 | 4 番目 | ・ ・ ・ | $n$ 番目 |
|---|---|---|---|---|---|---|
| 周の長さ (cm) | 4 | 10 | 16 | 22 | ・ ・ ・ | $\square$ |
周の長さは,
1 番目の $4$ cm に,番数が $1$ 増えるごとに $6$ cm ずつ足されていくと考えられます。
周の長さ
1 番目 ・・・ $4$ (cm)
2 番目 ・・・ $4+6\times \color{red}1$ (回)$=10$ (cm)
3 番目 ・・・ $4+6\times \color{red}2$ (回)$=16$ (cm)
4 番目 ・・・ $4+6\times \color{red}3$ (回)$=22$ (cm)
・
・
・
$n$ 番目 ・・・ $4+6\times \color{red} (n-1)$ (回)
上のように考えると,
$n$ 番目は 1 番目の長さにに $6$ cm を $(\,n-1\,)$ 回足した数になります。
よって,$n$ 番目の図形の 1 番下のカードの枚数は,
$4+6\times (\,n-1\,)=4+6n-6$
$=6n-2$ (cm)
(3)次の文章は,カードの総数について,花子さんの考えをまとめたものである。に $n$ を使った式をあてはまるように書きなさい。
3 番目の図形のカードの総数は,数えると $9$ 枚である。図 2 のように,3 番目の図形と,それをひっくり返した図形を組み合わせた図形を作り,計算で求めることもできる。図 2 の図形では,カードが $6$ 枚ずつ $3$ 段あるから,総数は $18$ 枚である。よって,3 番目のカードの総数は $9$ 枚である。
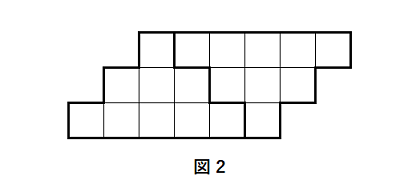
同じように考えると,$n$ 番目の図形のカードの総数は,枚となる。
解答・解説
解答$n^{2}$
花子さんの考え方では,
すべての段のカードの枚数が同じ枚数であり,
その枚数は,元の図形の一番上の枚数と一番下の枚数の和になっています。
また,段の数は番数と同じです。
$n$ 番目の図形についても,同じように考えると,
$1$ 段目の枚数は $1$ 枚,$n$ 段目の枚数は $2n-1$ (枚)だから,
各段の枚数は $=1+(\,2n-1\,)$ (枚)で,段数は $n$ 段です。
よって,$n$ 番目の図形のカードの総数は,
$\{\;1+(\,2n-1\,)\}\times n \times \dfrac{1}{\;2\;}=n^{2}$
(4)カードとカードの境目の長さの和は,3 番目の図形では $10$ cm である。$n$ 番目の図形では何 cm であるかを求めなさい。
解答・解説
解答$2n^{2}-3n+1$
まず,3 番目の図形について下の図のように考えます。
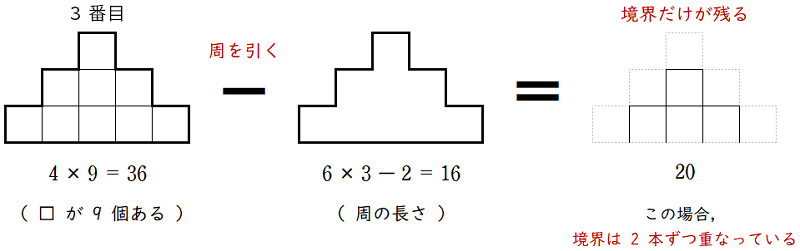
$1$ 枚のカードの周の長さは $4$ cmで,そのカードが $9$ 枚あるから,
周と境界の長さの和を,$4\times 9=36$ (cm) と考えます。
そして, 周と境界の長さの和から周だけの長さの和( $16$ cm )を引けば,
境界だけの長さの和( $20$ cm )が求められます。
ただしこの場合,
境界は上下左右の隣合ったカードの辺が $2$ つずつ重なっている
ことになります。
よって,境界の長さの和は,$20\times\dfrac{1}{\;2\;}=10$ (cm) となります。
この考え方で $n$ 番目の図形についても考えると,
$n$ 番目の図形のカードの数は $n^{2}$ 枚,周の長さは $(\,6n-2\,)$ cm だから,
$n$ 番目の図形の境界の長さの和 $=\{4\times n^{2}-(\,6n-2\,)\}\times \dfrac{1}{\;2\;}$
$=(\,4n^{2}-6n+2\,)\times \dfrac{1}{\;2\;}$
$=2n^{2}-3n+1$ (cm)

